Torus

Torus

Punktsettet i avstand fra den sirkulære linjen med radius danner en rotasjonsdreie.${\ displaystyle r}$${\ displaystyle R}$

En torus ( flertall tori, fra latin torus ) er et matematisk objekt fra geometri og topologi . Det er en perlelignende overflate med hull, så den har form av en tennisring , også en livbøye , dekk eller smultringer .

Eksempler på tori innebygd i tredimensjonalt rom er rotasjonsportene. Rotasjonsporter er revolusjonsflater som oppnås ved å rotere en sirkel rundt en akse som ligger i sirkelplanet og ikke krysser sirkelen. Hvis du ikke bare roterer den sirkulære linjen, men hele det sirkulære området , får du full torus .

En Rotationstorus fra at Med andre ord, mengden av prikker som dannes av en sirkulær linje med en radius av den faste avstand for å ha. ${\ displaystyle R}$${\ displaystyle r}$${\ displaystyle r <R}$

Torus oppnås ved å lime motsatte sider av et parallellogram

En torus kan også konstrueres ved å identifisere sidene til et parallellogram. Høyrekanten av parallellogrammet stiftes med venstre kant og overkant med underkant. Denne topologien brukes også av mange dataspill: hvis et spillobjekt forlater spillefeltet på den ene siden, dukker det opp igjen på motsatt side.

Begge konstruksjonene er spesielle tilfeller av den generelle matematiske definisjonen, som definerer en torus som det topologiske produktet av to sirkler. Dette begrepet spiller en rolle innen en rekke matematikkområder ; i tillegg til topologi og differensialgeometri, er det viktig i Fourier-analyse , teorien om dynamiske systemer ( invariant tori i himmelmekanikk ), funksjonsteori og teori om elliptiske kurver .

Rotasjonsporter gir en konkret, rotasjonssymmetrisk realisering av denne overflaten i det tredimensjonale euklidiske rommet . Innebygging annet enn en flat torus i firedimensjonalt rom er viktig for mange anvendelser innen teoretisk matematikk og fysikk . Dette har null krumning og maksimal symmetri .

Torus er en todimensjonal overflate . I matematikk vurderer man også -Torus mer generelt, en -dimensjonal manifold som generaliserer den todimensjonale torusen . Avvik fra dette, den tyskspråklige litteraturen bruker av og til også begrepene dobbel torus, trippel torus, etc. for områder med to, tre og flere hull. ${\ displaystyle n}$${\ displaystyle n}$

volum

Det volum av torusen kan beregnes som et volum integral ved hjelp av Jacobi determinant (den determinant av den funksjonelle matrise). Den Jacobi matrise for parameter av torusen kan bli gitt som følger:

${\ displaystyle J_ {f} = {\ frac {\ partial \ left (x, y, z \ right)} {\ partial \ left (r, t, p \ right)}} = {\ begin {pmatrix} \ delvis _ {r} x & \ delvis _ {t} x & \ delvis _ {p} x \\\ delvis _ {r} y & \ delvis _ {t} y & \ delvis _ {p} y \\\ delvis _ {r} z & \ delvis _ {t} z & \ delvis _ {p} z \\\ slutt {pmatrix}} = {\ begynn {pmatrix} \ cos (t) \ cos (p) & - R \ sin (t) - r \ sin (t) \ cos (p) & - r \ cos (t) \ sin (p) \\\ sin (t) \ cos (p) & R \ cos (t) + r \ cos (t) \ cos (p) & - r \ sin (t) \ sin (p) \\\ sin (p) & 0 & r \ cos (p) \ end {pmatrix}}}$

Det følger:

${\ displaystyle \ det (J_ {f}) = r \ cdot \ left (r \ cos (p) + R \ right)}$

Den funksjonelle determinanten her er derfor lik normen til overflatenormalvektoren.

${\ displaystyle V = \ int _ {V} \ mathrm {d} V = \ int _ {\ Gamma} \ det (J_ {f}) \ \ mathrm {d} \ Gamma = \ int _ {0} ^ { 2 \ pi} \ int _ {0} ^ {2 \ pi} \ int _ {0} ^ {r} \ left (Rr + r ^ {2} \ cos (p) \ right) \ \ mathrm {d} r \ \ mathrm {d} p \ \ mathrm {d} t = 2 \ pi ^ {2} r ^ {2} R}$

Så vi får for volumet av full torus . ${\ displaystyle V = 2 \ pi ^ {2} r ^ {2} R}$

Den formelen for volumet kan tolkes på en slik måte at den delen av den sirkel blir multiplisert med omkretsen (se Guldin nest regel ). For å forstå dette kan dette settes analogt med sylindervolumet . Det samme gjelder for den delen av overflaten, her utkant og multipliseres med hverandre (se Guldin First Rule ). Dette er også analogt med sylinderoverflaten . ${\ displaystyle A_ {r} = \ pi r ^ {2}}$ ${\ displaystyle U_ {R} = 2 \ pi R}$ ${\ displaystyle V _ {\ text {zyl}} = \ pi r ^ {2} l}$${\ displaystyle U_ {r} = 2 \ pi r}$${\ displaystyle U_ {R} = 2 \ pi R}$ ${\ displaystyle O _ {\ text {zyl}} = 2 \ pi rl}$

Hvis man bare ser på den indre delen av torusen, som er mindre enn eller lik avstanden fra aksen , blir resultatet volumet${\ displaystyle z}$${\ displaystyle R}$

${\ displaystyle \ int _ {0} ^ {2 \ pi} \ int _ {\ tfrac {\ pi} {2}} ^ {\ tfrac {3 \ pi} {2}} \ int _ {0} ^ { r} \ venstre (Rr + r ^ {2} \ cos (p) \ høyre) \ \ mathrm {d} r \ \ mathrm {d} p \ \ mathrm {d} t = \ pi r ^ {2} \ venstre (\ pi R - {\ tfrac {4r} {3}} \ høyre)}$

Den ytre delen av torusen, som er i en avstand større enn eller lik aksen , har volumet${\ displaystyle z}$${\ displaystyle R}$

${\ displaystyle \ int _ {0} ^ {2 \ pi} \ int _ {\ tfrac {3 \ pi} {2}} ^ {\ tfrac {\ pi} {2}} \ int _ {0} ^ { r} \ venstre (Rr + r ^ {2} \ cos (p) \ høyre) \ \ mathrm {d} r \ \ mathrm {d} p \ \ mathrm {d} t = \ pi r ^ {2} \ venstre (\ pi R + {\ tfrac {4r} {3}} \ høyre)}$

flate

Overflaten på torusen med den parametriske representasjonen ovenfor er

${\ displaystyle A_ {O} = 4 \ pi ^ {2} rR}$

Denne formelen kan enten være avledet fra Guldins første regel

${\ displaystyle A_ {O} = 2 \ pi r \ cdot 2 \ pi R}$

eller ved hjelp av overflateintegralet

${\ displaystyle A_ {O} = \ iint \ mathrm {d} A = \ int _ {t = 0} ^ {2 \ pi} \ int _ {p = 0} ^ {2 \ pi} r (R + r \ cos (p)) \ \ mathrm {d} p \ \ mathrm {d} t}$

å beregne. Det er den flate del av torusen i ovennevnte parameterrepresentasjon . ${\ displaystyle \ mathrm {d} A = r (R + r \ cos (p)) \ \ mathrm {d} p \ \ mathrm {d} t}$

Torus grenser til en tredimensjonal full torus . Den volumet av hele torus er (se Guldin Second Rule ). ${\ displaystyle V = 2 \ pi ^ {2} r ^ {2} R}$

Hvis man bare ser på den indre delen av torusen, som er mindre enn eller lik avstanden fra aksen , blir overflaten ${\ displaystyle z}$${\ displaystyle R}$

${\ displaystyle \ int _ {t = 0} ^ {2 \ pi} \ int _ {p = {\ tfrac {\ pi} {2}}} ^ {\ tfrac {3 \ pi} {2}} r ( R + r \ cos (p)) \ \ mathrm {d} p \ \ mathrm {d} t = 2 \ pi r \ left (\ pi R-2r \ right)}$

Den ytre delen av torusen, som er i en avstand større enn eller lik aksen , har overflaten ${\ displaystyle z}$${\ displaystyle R}$

${\ displaystyle \ int _ {t = 0} ^ {2 \ pi} \ int _ {p = {\ tfrac {3 \ pi} {2}}} ^ {\ tfrac {\ pi} {2}} r ( R + r \ cos (p)) \ \ mathrm {d} p \ \ mathrm {d} t = 2 \ pi r \ left (\ pi R + 2r \ right)}$

Torus som en overflate av revolusjon

En Rotationstorus er en revolusjonsflate dannet ved å rotere en sirkel rundt et horisontalt plan i sirkelen, og sirkelen som ikke krysser rotasjonsaksen , genereres. En dreiningskraft kan beskrives som settet med punkter som er i en fast avstand fra en sirkulær linje med en radius , hvor er. I kartesiske koordinater , med z-aksen som rotasjonsakse og sentrene til den roterende sirkelen i xy-planet, er den gitt av ligningen ${\ displaystyle R}$ ${\ displaystyle r}$${\ displaystyle r <R}$ ${\ displaystyle x, y, z}$

${\ displaystyle \ left ({\ sqrt {x ^ {2} + y ^ {2}}} - R \ right) ^ {2} + z ^ {2} = r ^ {2}}$

beskrevet. Eliminering av roten gir ligningen av grad 4

${\ displaystyle \ left (x ^ {2} + y ^ {2} + z ^ {2} + R ^ {2} -r ^ {2} \ right) ^ {2} = 4R ^ {2} \ left (x ^ {2} + y ^ {2} \ høyre).}$

En toroidal koordinat og en poloidal koordinat vinkelrett på den kan introduseres i den toroidale overflaten . Torus antas å ha blitt skapt av en sirkel som roteres rundt en akse som ligger i sirkelplanet. Vi kaller radiusen til den opprinnelige sirkelen , denne sirkelen danner også en koordinatlinje av . Vi kaller avstanden til sentrum av sirkelen fra aksen , koordinatlinjene for er sirkler rundt rotasjonsaksen . Begge koordinatene er vinkler og går fra til . ${\ displaystyle t}$${\ displaystyle p}$${\ displaystyle r}$${\ displaystyle p}$${\ displaystyle R}$${\ displaystyle t}$${\ displaystyle 0}$${\ displaystyle 2 \ pi}$

En radiell ...

... og en diagonalt kuttet torus i 3D

Parameterisering

Konverteringen av torus- koordinater til kartesiske koordinater er

${\ displaystyle {\ begin {pmatrix} x \\ y \\ z \ end {pmatrix}} = R \ cdot {\ begin {pmatrix} \ cos (t) \\\ sin (t) \\ 0 \ end { pmatrix}} + r \ cdot {\ begynn {pmatrix} \ cos (t) \ cdot \ cos (p) \\\ sin (t) \ cdot \ cos (p) \\\ sin (p) \ end {pmatrix }} = {\ begin {pmatrix} (R + r \ cdot \ cos (p)) \ cos (t) \\ (R + r \ cdot \ cos (p)) \ sin (t) \\ r \ cdot \ sin (p) \ end {pmatrix}}}$

Torus-koordinater er viktige i kjernefusjonsteknologi, se kjernefusjonsreaktor .

Fly kutt

1. Seksjoner med plan som inneholder den dreieakse er par av sirkler.
2. Seksjoner med plan som er vinkelrett på rotasjonsaksen er par av sirkler eller en sirkel eller tom.
3. Et plan parallelt med rotasjonsaksen skjærer en spiralkurve fra en torus . I spesielle tilfeller kan dette være en Cassini-kurve .
4. Et skråplan som berører to produsentsirkler kutter ut Villarceau-sirkler .

Tori i beskrivende geometri

I beskrivende geometri brukes deler av en torus til å konstruere overgangsflater mellom sylindere . Representasjonen av en torus gjennom omrisset kan bli funnet i omrisskonstruksjoner .

generell definisjon

Den todimensjonale torusen som et produkt av to sirkler.

Med blitt fylket ( 1-sfæren kalt). Den torus defineres da ved ${\ displaystyle \ mathbb {S} ^ {1}}$${\ displaystyle n}$

${\ displaystyle \ mathbb {T} ^ {n}: = \ underbrace {\ mathbb {S} ^ {1} \ times \ cdots \ times \ mathbb {S} ^ {1}} _ {n \ {\ text { ganger}}}}$,

hvor er det produkt av topologiske rom . Som beskrevet i forrige avsnitt er revolusjonens overflate en 2-torus. 2-torus kalles vanligvis bare torus.${\ displaystyle \ times}$

Topologiske egenskaper

Struktur av en manifold

Den torus er et topologisk manifold . Dette følger av det faktum at torus er det topologiske produktet av 1- sfærer, og selve 1-sfæren er en topologisk manifold. 1-sfæren er også en differensierbar manifold, og siden produktet av differensierbare manifolder resulterer i en differensierbar manifold, er torus også en differensierbar manifold. Den dimensjon av er den samme . ${\ displaystyle n}$${\ displaystyle n}$${\ displaystyle n}$${\ displaystyle n}$${\ displaystyle \ mathbb {T} ^ {n}}$${\ displaystyle n}$

Topologiske egenskaper

Det følger også direkte av definisjonen at torus er kompakt . I tillegg er det stierelatert . I motsetning til sfæren er ikke torus bare koblet for . ${\ displaystyle n}$${\ displaystyle n}$${\ displaystyle n}$${\ displaystyle n> 1}$

Den kartlegging , definert av , er den universelle overlegg av den torus.${\ displaystyle q \ colon \ mathbb {R} ^ {n} \ to \ mathbb {T} ^ {n}}$${\ displaystyle (x_ {j}) _ {j}: = (\ exp (2 \ pi \ mathrm {i} x_ {j})) _ {j}}$${\ displaystyle n}$

Løgnegruppe

1- sfæren , forstått som en sirkelgruppe , er også en løgngruppe . Siden produktet av flere Lie-grupper med den komponentvise multiplikasjonen igjen er en Lie-gruppe, er -Torus også en Lie-gruppe.${\ displaystyle n}$

Innebygd tori

Flat tori

Modell av en flat torus: papiret trenger bare å bøyes, ikke strekkes.

Siden den sirkulære linjen åpenbart kan være innebygd i , kan torus forstås som en delmengde av det euklidiske rommet . Man ser på den Riemannisk metrisk , som er indusert ved den euklidske metrisk på plass på torusen. Denne beregningen er flat , det vil si at torus er lokalt isometrisk til et nabolag i . Spesielt er skjæringskurvaturen derfor konstant null overalt. Siden torusen er kompakt og derfor også komplett , er den en flat manifold . Man snakker derfor om en flat torus. ${\ displaystyle \ mathbb {S} ^ {1}}$${\ displaystyle \ mathbb {R} ^ {2}}$ ${\ displaystyle n}$${\ displaystyle \ mathbb {T} ^ {n}: = \ mathbb {S} ^ {1} \ times \ cdots \ times \ mathbb {S} ^ {1} \ subset \ mathbb {R} ^ {2n}}$ ${\ displaystyle \ mathbb {R} ^ {2n}}$${\ displaystyle \ mathbb {T} ^ {n}}$ ${\ displaystyle g}$${\ displaystyle \ mathbb {R} ^ {2n}}$${\ displaystyle n}$ ${\ displaystyle g}$${\ displaystyle n}$${\ displaystyle \ mathbb {R} ^ {n}}$${\ displaystyle n}$${\ displaystyle n}$

Det er andre flate beregninger på torusen i tillegg til den som er beskrevet ovenfor . Flat 2-tori kan beskrives med et parallellogram , hvor motsatte sider er limt sammen. Tilsvarende kan flat tori beskrives som topologiske grupper av faktorer for to lineært uavhengige vektorer . I det spesielle tilfellet og man får kvotienten . ${\ displaystyle \ mathbb {R} ^ {2} / (\ mathbb {Z} \ cdot v + \ mathbb {Z} \ cdot w)}$ ${\ displaystyle v, w \ in \ mathbb {R} ^ {2}}$${\ displaystyle v = (1,0)}$${\ displaystyle w = (0.1)}$ ${\ displaystyle \ mathbb {R} ^ {2} / \ mathbb {Z} ^ {2} \ cong (\ mathbb {R} / \ mathbb {Z}) ^ {2}}$

Elliptiske kurver over de komplekse tallene kan vises ved hjelp av Weierstrassian-parameteriseringen som for et rutenett og er derfor (med en oversettelses-invariant metrisk ) eksempler på flat tori. Den modul plass av de elliptiske kurver eller tilsvarende av den flate 2-tori er den såkalte modul kurve . ${\ displaystyle \ mathbb {C} / L}$ ${\ displaystyle L \ subset \ mathbb {C}}$

Flat tori i tredimensjonalt rom

En dobbel differensierbar innebygging av torusen i et tredimensjonalt rom kan ikke være flat fordi det lokale ekstremet må være punkter med positiv krumning . I følge Nashs innebygde teorem er det imidlertid fraktale (bare en gang differensierbare ) innlejringer av den flate torusen i et tredimensjonalt rom . Disse kan også konstrueres numerisk.

Rotasjonsport i tredimensjonalt rom

En rotasjons torus er en innebygd 2-torus, som kan beskrives som et sett med punkter som er i en fast avstand fra en sirkulær linje med en radius , hvor er. ${\ displaystyle \ mathbb {R} ^ {3}}$ ${\ displaystyle R}$ ${\ displaystyle r}$${\ displaystyle r <R}$

Clifford Tori

En Clifford torus er en spesiell torus innebygd i den. Etter identifisering og standarden kan Cliffordtorus beskrives som ${\ displaystyle S ^ {3} \ subset \ mathbb {R} ^ {4}}$${\ displaystyle \ mathbb {R} ^ {4} = \ mathbb {C} ^ {2}}$${\ displaystyle S ^ {3} = \ left \ {(z, w) \ in \ mathbb {C} ^ {2} \ colon | z | ^ {2} + | w | ^ {2} = 1 \ right \}}$

${\ displaystyle T: = \ left \ {(z, w) \ in \ mathbb {C} ^ {2} \ colon | z | = | w | = {\ frac {1} {\ sqrt {2}}} \ right \} \ delmengde S ^ {3}}$.

Videre blir bildene av under isometriske standardmetriske referert til som Clifford tori. ${\ displaystyle T}$${\ displaystyle A \ i O (3) = \ operatorname {isom} (S ^ {3})}$

Ved hjelp av stereografisk projeksjon kan man også forstå Clifford tori som innebygd i tori. ${\ displaystyle \ mathbb {R} ^ {3}}$

En Clifford torus er et minimalt område med hensyn til standard beregning på . Lawson-antagelsen, bevist av Brendle , sier at hver minimal overflate i den innebygde torusen er en Clifford-torus. ${\ displaystyle S ^ {3}}$${\ displaystyle S ^ {3}}$

Konstruksjon fra en firkant eller kube

Konstruksjon av todimensjonal tori fra et kvadratisk eller parallellogram

Torus hentes fra et kvadrat ved å lime motsatte sider.

Egenskapene til 3-torus

I motsetning til overflaten til en kule kan torusen kartlegges på en flat, rektangulær overflate uten singulariteter .

Høyrekanten av rektangelet eller firkanten er sydd til venstre kant og nedre kant sydd til øvre kant. Denne konstruksjonen fungerer også med hvilket som helst parallellogram . Mange dataspill, for eksempel asteroider eller Pac-Man , har også denne topologien : Hvis et spillobjekt forlater spillefeltet på den ene siden, vises det igjen på motsatt side.

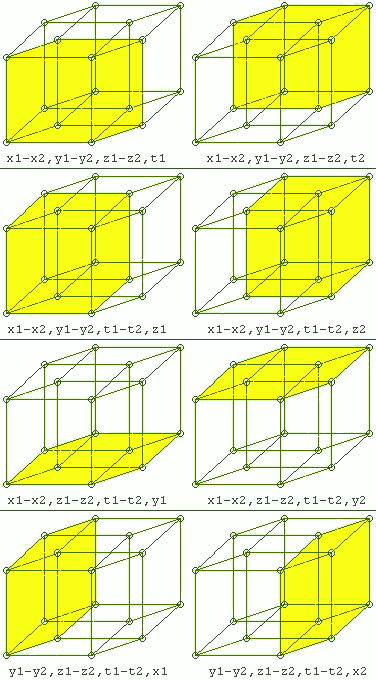
Konstruksjon av høyere dimensjonale tori fra en kube eller parallellpiped

Den tredimensjonale torus eller 3-torus er en parallellpiped eller kube , hvis seks motsatte flater er festet til hverandre parvis.

Den firedimensjonale torusen eller 4-torusen er en tesserakt , hvor de åtte motsatte terningene sitter sammen parvis.

Generelt er den -dimensjonale torusen en -dimensjonal kube hvis motsatte - hyperkubber er identifisert med hverandre parvis. Du kan også representere det som . ${\ displaystyle n}$${\ displaystyle n}$${\ displaystyle [0,1] ^ {n}}$${\ displaystyle (n-1)}$${\ displaystyle \ mathbb {R} ^ {n} / \ mathbb {Z} ^ {n}}$

Også her, i stedet for en -dimensjonal kube , kan hvilken som helst -dimensjonal parallellpiped brukes til å konstruere en -dimensjonell torus ved å identifisere sidene . ${\ displaystyle n}$${\ displaystyle n}$${\ displaystyle n}$

Sju fargesett

Overflaten på en torus kan deles inn i 7 områder slik at to områder berører hverandre. For å fargelegge dette kartet slik at ikke to tilstøtende områder får samme farge, kreves det 7 farger.

Animasjon av en torus. Overflaten er delt inn i 7 områder med forskjellige farger.

Syvfargesetningen for torus sier at 7 farger alltid er tilstrekkelig til å fargelegge hvilket som helst kart på overflaten av en torus på en slik måte at ingen to naboland får samme farge.

Dette betyr at hver graf som kan bygges inn i torusen har et kromatisk antall på maksimalt 7 (se nodefarging ). Fordi den komplette grafen kan legges inn i torusen, er det kromatiske tallet 7.${\ displaystyle K_ {7}}$

Færre farger er tilstrekkelig i planet eller på en sfærisk overflate . Den fire-farge teorem sier at fire farger er alltid tilstrekkelig for å farge noen kart i euklidske planet på en slik måte at to nabolandene få samme farge.

Algebraisk torus

I teorien om algebraiske grupper , er torus brukes i en annen forstand. Der betyr det en gruppe som er isomorf til et endelig produkt av kopier av multiplikasjonsgruppen til en kropp . For avgrensningsformål snakker man om en algebraisk torus i motsetning til en topologisk torus.

For eksempel i torisk geometri , studiet av toriske varianter , er torus vanligvis en algebraisk torus.

Søknadseksempler

En livbøye har formen av en torus.

En livbøye med en ytre diameter på 76 centimeter og en indre diameter på 44 centimeter har formen av en torus. Så den har den faste avstanden fra en sirkulær linje med radiusen . ${\ displaystyle r = (76 \ \ mathrm {cm} -44 \ \ mathrm {cm}) / 4 = 8 \ \ mathrm {cm}}$ ${\ displaystyle R = (76 \ \ mathrm {cm} +44 \ \ mathrm {cm}) / 4 = 30 \ \ mathrm {cm}}$

Dette resulterer i volum og overflate :

• Volum :${\ displaystyle V = 2 \ cdot \ pi ^ {2} \ cdot r ^ {2} \ cdot R = 2 \ cdot \ pi ^ {2} \ cdot (8 \ \ mathrm {cm}) ^ {2} \ cdot 30 \ \ mathrm {cm} \ ca. 37899 \ \ mathrm {cm ^ {3}} = 0 {,} 037899 \ \ mathrm {m ^ {3}}}$

• Overflate :${\ displaystyle A_ {O} = 4 \ cdot \ pi ^ {2} \ cdot r \ cdot R = 4 \ cdot \ pi ^ {2} \ cdot 8 \ \ mathrm {cm} \ cdot 30 \ \ mathrm {cm } \ ca 9475 \ \ mathrm {cm ^ {2}} = 0 {,} 9475 \ \ mathrm {m ^ {2}}}$

Se også

• Prikket torus
• Torus knute
• Stanford torus
• Torus antenne
• Spindel torus
• Dupins syklider

litteratur

• Marcel Berger : Geometry I. Oversatt fra 1977 fransk original av M. Cole og S. Levy. Universitetstekst. Springer-Verlag, Berlin, 2009. ISBN 978-3-540-11658-5 .
• Anatole Katok , Vaughn Climenhaga: Forelesninger på overflater. (Nesten) alt du ønsket å vite om dem. Student Mathematical Library, 46th American Mathematical Society, Providence, RI; Mathematics Advanced Study Semesters, University Park, PA, 2008. ISBN 978-0-8218-4679-7 .

weblenker

Wiktionary: Torus  - forklaringer på betydninger, ordets opprinnelse, synonymer, oversettelser

• Eric W. Weisstein : Torus . På: MathWorld (engelsk).
• Mathcurve: torus
• Matematikkfletting: torus

Individuelle bevis

1. ^ Karl Ernst Georges : Omfattende latin-tysk kortfattet ordbok . 8., forbedret og økt utgave. Hahnsche Buchhandlung, Hannover 1918 ( zeno.org [åpnet 26. juni 2019]). 
2. ↑ Det er en rekke andre historiske bruksområder for begrepet torus som ikke lenger er i bruk i dag : Herder 1854, Pierer 1857, Meyers 1905, Brockhaus 1911, Britannica 1911.
3. ^ Bronstein, Semendjajew: Taschenbuch der Mathematik. Harri Deutsch Verlag (1983), ISBN 3871444928 , s. 253.
4. ^ Ulrich Graf , Martin Barner : Descriptive Geometry. Quelle & Meyer, Heidelberg 1961, ISBN 3-494-00488-9 , s. 202, 209.
5. ↑ C. Leopold: Geometriske grunnleggende om arkitektonisk representasjon. Verlag W. Kohlhammer, Stuttgart 2005, ISBN 3-17-018489-X , s. 123, 129.
6. ^ John M. Lee: Introduction to Smooth Manifolds (= Graduate Texts in Mathematics 218. ) Springer-Verlag, New York NY et al. 2003, ISBN 0-387-95448-1 , s. 8.
7. ^ John M. Lee: Introduction to Smooth Manifolds (= Graduate Texts in Mathematics 218. ) Springer-Verlag, New York NY et al. 2003, ISBN 0-387-95448-1 , s. 21.
8. ^ Tammo tom Dieck: Topologi. de Gruyter, Berlin, 2000, ISBN 3-11-016236-9 , s. 52.
9. ^ John M. Lee: Introduction to Smooth Manifolds (= Graduate Texts in Mathematics 218. ) Springer-Verlag, New York NY et al. 2003, ISBN 0-387-95448-1 , s. 39.
10. ^ John M. Lee: Introduction to Smooth Manifolds (= Graduate Texts in Mathematics 218. ) Springer-Verlag, New York NY et al. 2003, ISBN 0-387-95448-1 , s. 289.
11. ↑ V. Borrelli, p Jabrane, F. Lazarus, B. Thibert: Flat tori i tredimensjonalt rom og konveks integrasjon. ( Memento fra 1. juli 2012 i Internet Archive ). Proc. Natl. Acad. Sci. USA 109 (2012), nr. 19, 7218-7223.
12. ↑ CNRS pressemelding : Mathématiques: première image d'un tore plat en 3D. 20. april 2012.
13. ^ Wolfram MathWorld: Torus Coloring
14. ↑ Chelsey Pöttker, Southern Illinois University Edwardsville: Topology and the Four Color Theorem
15. ^ Wolfram MathWorld: Four-Color Theorem
16. ^ Neil Robertson, Daniel P. Sanders, Paul Seymour, Robin Thomas, Georgia Institute of Technology: The Four Color Theorem
17. ^ Oda: Forelesninger om Torus innebygging og applikasjoner. 1978, 1.1 Algebraisk tori.