torget

Firkant med sidelengde a og diagonal d

I geometri er et kvadrat en spesiell polygon , nemlig en flat, konveks og vanlig firkant . Den har fire sider med like lengde og fire rette vinkler . Firkanten er et spesielt tilfelle av rektangelet , diamanten , parallellogrammet , trapesformen og dragen . For bygging av et kvadrat er en indikasjon tilstrekkelig, f.eks. B. lengden på siden eller diagonalen .

Kvadrater er ansiktene til et platonisk fast stoff , nemlig kuben . Torget er også den grunnleggende formen for en platonisk flislegging . Som et spesielt tilfelle av tilsvarende generelle n- dimensjonale legemer , er firkanten både den todimensjonale hyperkuben og den todimensjonale krysspolytopen .

eiendommer

Følgende gjelder torget:

• De fire sidene har samme lengde, det vil si at det er en diamant og en ligesidig polygon .
• De fire innvendige vinklene er de samme, det vil si at det er et rektangel og en ekvivalent polygon . De innvendige vinklene er rette vinkler .
• De to diagonalene er like lange, halverer hverandre og er ortogonale .
• Den krysset av diagonalen er innenfor - og innskrevne sirkel-midtpunktet og midten av symmetri . Torget er både en akkord og en tangent firkant .
• Den delen av den omkrets er dobbelt så stor som den innskrevet sirkel .
• Den har 4 akser av symmetri : de to vertikale og de to diagonalene .
• Den er firdobbelt rotasjonssymmetrisk og derfor også punktsymmetrisk .
• Den symmetri-gruppen er to-plans-gruppen .${\ displaystyle D_ {4}}$

Torget kan karakteriseres som:

• Rektangel med to tilstøtende sider av samme lengde
• Diamant med to tilstøtende like vinkler
• Diamant med rett vinkel
• Parallelogram med to tilstøtende sider av samme lengde og to tilstøtende like vinkler
• Parallelogram med to tilstøtende sider av lik lengde og rett vinkel
• Firkantet med ortogonale diagonaler av samme lengde som halverer hverandre

Formler

Matematiske formler i kvadrat
Område	${\ displaystyle A = a ^ {2} = {\ frac {d ^ {2}} {2}}}$
omfang	${\ displaystyle U = \, 4 \ cdot a}$
Lengde på diagonalene	${\ displaystyle d = a \ cdot {\ sqrt {2}} = 2 \ cdot r_ {u}}$
Innskrevet radius	${\ displaystyle r_ {i} = {\ frac {a} {2}} = {\ frac {d} {2 \ cdot {\ sqrt {2}}}}}$
Omkretsradius	${\ displaystyle r_ {u} = {\ frac {a} {\ sqrt {2}}} = {\ frac {d} {2}}}$
Innvendig vinkel	${\ displaystyle \ alpha = \ beta = \ gamma = \ delta = 90 ^ {\ circ}}$

konstruksjon

Torget er en vanlig polygon som kan konstrueres med et kompass og linjal .

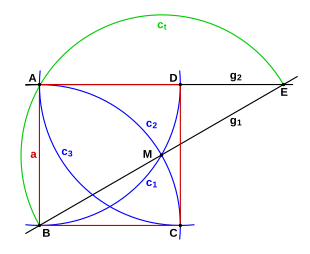
Konstruksjon med en gitt sidelengde

Konstruksjon med en gitt side, klarer seg med en enkelt kompassinnstilling (radius = a)

1. Gitt: Siden a med endepunktene A og B.
2. Tegn en bue rundt enden A (c ₁ , minst en kvart sirkel) med sidelengden som radius.
3. Tegn en bue rundt enden B (c ₂ , minst en kvart sirkel) med sidelengden som radius. Krysset mellom sirklene er punkt M.
4. Tegn en rett linje gjennom punktene B og M (minst dobbelt så lenge som BM )
5. Tegn en Thales-sirkel (c _t ) rundt M til B. Du får punkt E.
6. Tegn en rett linje gjennom punktene A og E. Skjæringspunktet med c ₁ er hjørne D på den senere firkanten.
7. Tegn rundt D på den ene buen (c ₃ ) med sidelengden som radius. Krysset med c ₂ er hjørne C.
8. Koble hjørnene for å danne en firkant.

Konstruksjon med en gitt diagonal

Konstruksjon for en gitt diagonal

1. Gitt: Diagonalen d med endepunktene A og C.
2. Konstruer den vertikale linjen (blå) på diagonalen. Skjæringspunktet med diagonalen er midtpunktet M.
3. Tegn en sirkel rundt M gjennom A. Skjæringspunktene med vinkelrett er de to manglende hjørnene B og D.
4. Koble hjørnene A, B, C og D syklisk.

Animasjoner

Firkant med en gitt sidelengde bruker Thales-sirkelen. Det fungerer også med et annet midtpunkt M, animasjon		Firkantet med en gitt diagonal, animasjon

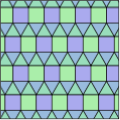
Flislegging med firkanter

Noen platoniske og arkimediske fliser inneholder firkanter. Disse fliser er periodiske, rotasjonssymmetriske og translasjonssymmetriske og inneholder bare vanlige polygoner .

• 

  Firkantet rutenett

• 

  3-3-3-4-4

• 

  3-3-4-3-4

• 

  3-4-6-4

• 

  4-8-8

• 

  4-6-12

Tallene under figurene viser hvor mange hjørner de vanlige polygonene har, som hver møtes på et punkt . Innvendige vinkler legger opp til 360 °.

Polyhedron med firkanter

Den kuben er den eneste Platonsk legeme som har kvadratiske flater . Noen arkimediske faste stoffer inneholder også firkanter, for eksempel kuboktaheder , avkortet oktaeder , rhombisk kubokeder og rhombicosidodecahedron .

• 

  terning

• 

  Cuboctahedron

• 

  Avkortet oktaeder

• 

  Diamond cuboctahedron

• 

  Rhombicosidodecahedron

Generaliseringer

I euklidisk geometri er firkanten det todimensjonale spesielle tilfellet av hyperkubber og krysspolytoper .

Uttrykket kvadrat er i den syntetiske geometrien av affinplanet generalisert av en av de tilsvarende utsagnene som beskriver et kvadrat i den elementære geometrien, brukes til definisjonen av begrepet. For eksempel for nivåer før euklidene blir eksistensen av disse figurene et ekstra aksiom .

I ikke-euklidiske geometrier er firkanter vanligvis polygoner med 4 sider av samme lengde og like indre vinkler .

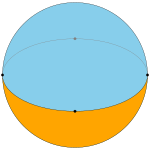
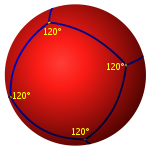
I sfærisk geometri er et kvadrat en polygon hvis sider er store sirkler som krysser i samme vinkel . I motsetning til kvadrater med plan geometri , er vinklene til et sfærisk firkant større enn en rett vinkel . Større sfæriske firkanter har større vinkler.

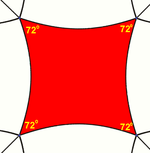
I den hyperbolske geometrien eksisterer ikke firkanter med rette vinkler . I stedet har firkanter vinkler som er mindre enn en rett vinkel. Større hyperbolske firkanter har mindre vinkler.

Generaliseringer av torget
geometri	sfærisk geometri	sfærisk geometri	Euklidisk geometri	hyperbolsk geometri
Innvendig vinkel	180 °	120 °	90 °	72 °
Schäfli-symbol	{4, 2}	{4, 3}	{4, 4}	{4, 5}
Antall firkanter i fliser	2	Sjette	uendelig	uendelig

Latinsk firkant

Et latinsk kvadrat er et kvadratisk skjema med n rader og kolonner, hvor hvert felt er okkupert av en av n forskjellige symboler, slik at hvert symbol vises nøyaktig en gang i hver rad og i hver kolonne. Det naturlige tallet n kalles rekkefølgen på det latinske torget.

Eksempler

${\ displaystyle {\ begin {bmatrix} 1 & 2 & 3 \\ 3 & 1 & 2 \\ 2 & 3 & 1 \ end {bmatrix}} \ quad {\ begin {bmatrix} 1 & 2 & 3 & 4 \ \ 2 & 3 & 4 & 1 \\ 3 & 4 & 1 & 2 \\ 4 & 1 & 2 & 3 \ end {bmatrix}}}$

Magisk torg

Et magisk firkant med kantlengde 3

Et magisk kvadrat med kantlengde n er et kvadratisk arrangement av de naturlige tallene 1, 2,…, n², der summen av tallene til alle rader, kolonner og de to diagonalene er de samme. Denne summen er kjent som det magiske kvadratets magiske nummer .

Kvadrering av torget

Enkel , perfekt firkant av kvadratet i lavest mulig rekkefølge (21)

Kvadraturet på firkanten er flislegging av et gitt kvadrat med mindre firkanter hvis sidelengder har heltallverdier . Oppgaven blir interessant og krevende på grunn av følgende tilleggsvilkår:

• Ingen to underruter skal ha samme størrelse. En firkantet flislegging som oppfyller dette kravet kalles perfekt .
• Hvis en delmengde av underkvadratene danner et rektangel , kalles kvadraturet sammensatt , ellers enkelt .

Kvadrat sirkelen

Firkanten og sirkelen har samme område .

Kvadrering av sirkelen er et klassisk problem i geometri. Oppgaven er å konstruere en firkant med samme areal fra en gitt sirkel i endelig mange trinn . Det tilsvarer den såkalte korrigering av sirkelen , dvs. konstruksjonen av en rett linje som tilsvarer sirkelens omkrets. Dette tilsvarer igjen konstruksjonen av sirkelnummeret fra segmentet 1. Hvis man begrenser konstruksjonsmidlene til linjaler og kompasser , er oppgaven uløselig på grunn av transcendensen av . Dette ble bevist i 1882 av den tyske matematikeren Ferdinand von Lindemann . ${\ displaystyle \ pi}$${\ displaystyle \ pi}$

weblenker

Wiktionary: kvadrat  - forklaringer av betydninger, ordets opprinnelse, synonymer, oversettelser

• Kvadrat rektangelet
• Kvadratur polygonen
• Animert læringssekvens (konstruksjon, omfang, område)