Eulers leirnett
Den Euler notasjon er oppkalt etter matematikeren Leonhard Euler , som introduserte den for den fine analyse av musikkstykker i ren tuning . Det fremgår allerede av betegnelsen om de forekommende tredjedeler og femtedeler høres rene ut. For eksempel har tonic, subdominant og dominerende akkorder av den rene C durskalaen representasjonen c -, e - g og f-, ac samt g-, hd (dur akkorder med en ren dur og mindre tredjedel og en ren femte), hvor "lavpunktet" før , e og , a så vel som , h betyr at tonene høres et syntonisk komma lavere enn e og a så vel som h i serien med perfekte femtedeler ... fcgdaeh .. .
Den Euler tone gitter representerer skalaen av renstemmingens er i et to-dimensjonalt rutenett av ren femte og Terzintervallen. Euler hadde allerede i den offentliggjort i 1739. Tentamen novae theoriae musicae diskutert i detalj de matematiske relasjoner til musikk. I dette arbeidet lette han etter en matematisk begrunnelse for følelsen av konsonans og dissonans i musikkunsten og satt sammen et intervallforholdssystem på grunnlag av primtall. I et annet verk, De harmoniae veris principiis per speculum musicum repraesentatis , som ble utgitt i 1773, beskrev han tonennettverket til femtedeler og tredjedeler.
Femte-tredje ordningen
Innføringen av den rene stor ters (med strengen lengdeforholdet mellom nedre og øvre tone av 5: 4) - som en erstatning og forenkling av den pytagoreiske ditone (81:64) - går tilbake til Didymos' enharmonisk tetrakord divisjon (ca. 100 år etter Pythagoras ). Imidlertid kan tonesystemet i det gamle Hellas ikke sammenlignes med det tonesystemet som Leonhard Euler refererer til. I vårt nåværende tonesystem ble den rene store tredjedelen først nevnt rundt 1300 av Walter Odington i sine De Speculatione Musices .
I vestlig musikk ble den største tredjedelen (frekvensforhold: 81:64) av Pythagoras-systemet oppfattet som en dissonans. Med fremveksten av polyfoni på 1400-tallet ble den rene store tredjedelen (5: 4) stadig viktigere som en del av triaden.
C-dur akkord i overtone-serien?
Dette resulterer i et tonesystem basert på intervallene oktav 2 ⁄ 1 , femte 3 ⁄ 2 og tredje 5 ⁄ 4 . De andre intervallene i det femte-tredje systemet kan vises som multipler av disse intervallene.
Mangfoldet av kombinasjoner av disse intervallene resulterer i et (teoretisk) uendelig tonehøyde. Denne bek plass blir ofte representeres grafisk ved hjelp av en tonehøyde nettverk som følger:
Representasjon i fatnettverket
Siden den rene tredjedelen ikke kunne representeres med femtedeler, representerte Leonhard Euler nettverket av relasjoner for den rene innstillingen ved hjelp av rader med femtedeler, som hver for seg skilte seg med et syntonisk komma. I det følgende nettverket av relasjoner er femtedelen oppstilt i horisontal retning og tredjedeler i vertikal retning.
Notasjonen, x ("dyp komma x") eller 'x ("apostrof x") - komma foran tonebetegnelsen - osv. Betyr at tonen, x eller' x er et syntonisk komma lavere eller høyere enn tone x er.
Denne grafiske representasjonen av femte-tredje ordningen forstås som et nettverk av forhold mellom tonehøyde klasser uten fast oktav (også: "Chroma", "tonal character" ; engelsk tonehøyde klasse ), slik at for beregning av spesifikke intervallforhold eller tilsvarende multiplum av oktaven 2- / Anmeldelse for 1. tilsatt - eller må tas bort.
De rene skalaene har alltid samme utseende i denne grafiske fremstillingen. Intervallforhold er alltid de samme for alle skalaer:
| skala | Skaleringstoner oppført i en tabell | ||||||||||||||||
| F-dur | f | G | , a | b | c | , d | , e | f | , D-moll | , d | , e | f | , G | , a | b | c | , d |
| C-dur | c | d | , e | f | G | , a | , H | c | , En mindreårig | , a | , H | c | , d | , e | f | G | , a |
| G-dur | G | en | , H | c | d | , e | , fis | G | , E-moll | , e | , fis | G | , a | , H | c | d | , e |
| x dur | x | x | , x | x | x | , x | , x | x | x moll | x | x | 'x | x | x | 'x | 'x | x |
(For en mer omfattende tabell, se Vektene i sirkelen av femtedeler )
Beregningen av de tilsvarende centverdiene ved bruk av eksemplet med tonene c - e -, e med oktav = 1200 cent, femte = 701.955 cent og syntonisk komma = 21.506 cent resulterer for eksempel med c = 0 cent avrundet:
- e = c + 4 femtedeler - 2 oktaver = 408 cent og, e = e - syntonisk komma = 386 cent (= c + ren major tredjedel)
De tilsvarende frekvensverdiene beregnes med c = 264 Hz som følger:
- .
Cent-verdiene til tonene resulterer i:
| volum | beregning | Cent verdi |
|---|---|---|
| c | 0 | 0 |
| d | 2q - o | 204 |
| , e | 4q - 2o - k | 386 |
| f | −q + o | 498 |
| G | q | 702 |
| , a | 3q - o - k | 884 |
| , H | 5q - 2o - k | 1088 |
| c ′ | O | 1200 |
(For en mer omfattende tabell, se Vektene i sirkelen av femtedeler )
Det viser toneforholdene til det harmonisk-rene humøret . For eksempel høres tonene, e og, a og, h av C-durskala et syntonisk komma lavere enn i den pythagoriske femtedelskjeden . Akkordene c-, f.eks. Og f-, ac samt g-, hd består av rene tredjedeler ( 5 ⁄ 4 og 6 ⁄ 5 ) og perfekte femtedeler ( 3 ⁄ 2 ).
Selve "Tonnetz" ble introdusert i 1773 av Leonhard Euler som speculum musicum ("image of music") i sin eponyme skriving De harmoniae veris principiis per speculum musicum repraesentatis , og fra da av - sammen med betegnelsene introdusert av Moritz Hauptmann for tidligere eponyme toner som skiller seg med et syntonisk komma - modifisert av mange teoretikere for forskjellige formål (inkludert av Hermann v. Helmholtz , Arthur v. Oettingen og Hugo Riemann ). De forskjellige tegnene i toner med samme navn, men forskjellige posisjoner i (uendelig) tonehøyde, resulterer i en harmonisk-ren tuning, ikke bare fra et annet tonemiljø og harmonisering (f.eks., E i C-dur akkord c-, f.eks. Og e i E-dur akkord e-, g skarp-b), men også fra en (minimal) tonehøydeforskjell mellom de respektive tonene (, e og e):
I C-durskalaen er cd, efg, a, hc, intervallet c-, e en stor tredjedel med et frekvensforhold på 5 ⁄ 4 . I serien femtedeler cgdae er intervallet (oktav bak) ce en Pythagoras tredjedel med frekvensforholdet 81 ⁄ 64 . Disse to intervaller avviker med den syntonic komma med den frekvensforhold 81 / 80 .
C-dur skalaen i en harmonisk, ren femte-tredje innstilling
Den rene C-durskalaen kan forstås som utvalget av de syv tonene fra det femte og tredje skjemaet som brukes til intonasjon av de tre hovedfunksjonene subdominant (S), tonic (T) og dominant (D) - dvs. for "autentisk" tråkkfrekvens er nødvendig:
C major tonalitet
Den faktiske skalaen opprettes ved å transponere disse tonene i det tilsvarende oktavområdet - for eksempel mellom c 1 og c 2 . I motsetning til den pythagoriske skalaen består den ikke lenger av to, men tre intervalltrinn av forskjellige størrelser, den store heltonen 9 ⁄ 8 , den lille heltonen 10 ⁄ 9 og den diatoniske halvtonen 16 ⁄ 15 :
ren C durskala
Avhandlingen (for eksempel av Sigfrid Karg-Elert ) at med denne sju-trinns skalaen, som tillater harmonisk ren intonasjon av hovedfunksjonene T, S og D, melodisk uren, fordi de respektive tredjedeler, e /, a og, h i melodisk sammenheng kan oppfattes som for lavt er kontroversielt. Ross W. Duffin beviser at den "uttrykksfulle intonasjonen", jeg. H. bruken av skjerpte ledende toner, særlig siden Pablo Casals (1876–1973) har vært et grundig moderne fenomen. Han nevner for eksempel: Hermann von Helmholtz , som fysisk undersøkte Joseph Joachims spill , fant at Joachim intonerte tredjedelen (nesten) rent, noe som også bekreftes i hans opptak fra 1903 - til tross for tekniske mangler.
Bruk av Eulers lydnettverk for fin musikalsk analyse
Se også detaljert analyse for intonasjonsproblemer
Eksempel 1: triade på andre nivå i C-dur
Sammenligning av de to triadene
- Triade på 2. grad , d - f -, a (moll akkord med en ren moll og dur tredje) og
- Triade på 5. grad g -, b - d (dur akkord med en ren dur og mindre tredjedel)
du kan umiddelbart se at tonene d og d skiller seg ut med et syntonisk komma.
Se også eksempel 3.
Eksempel 2: Forskjell G skarp og A flat
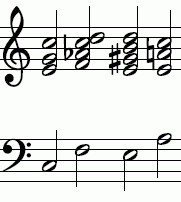
|
Akkorder (med frekvenser i Hertz)
C dur tonic: c (132) c '(264), e' (330) g '(396) c ″ (528) C-dur underdominant i moll med seksti ajoutée : f (176) f ′ (352) 'som ′ (422.4) c ″ (528) d ″ (594) En mindre dominerende syvende akkord :, e (165), e ′ (330) ,, g skarp ′ (412,5), h ′ (495) d ″ (586,7) En mindre tonic :, a (220), e ′ (330), a ′ (440) c ″ (528) Som det er 9,9 Hz høyere enn G skarpt med frekvensforholdet AS / G skarpt = 128 ⁄ 125 (41 cent). Dette intervallet er den lille Diësis . |
Eksempel 3: "Kommafellen"
Kor som lytter til hverandre spesielt godt, kan detonere. Dette skyldes ofte den forskjellige intonasjonen av toner med samme navn. Dette har vært kjent lenge. Den detaljerte musikalske analysen om den, som er lettere å forstå ved hjelp av navnene på Eulers lydnettverk, er ikke en del av den musikalske utdannelsen.
Et klassisk eksempel på en "komma-felle" er forekomsten av andregrads akkord:
Det tredje akkordet f-, ad høres urent ut i C-dur. Et kor der stemmene lytter til hverandre synger passende d a syntonisk komma lavere, her betegnet av, d. Det handler om moll parallell med F dur akkord og F dur skalaen er fg-, bc- , d- , ef. I det følgende akkordet g-, hd må imidlertid den “korrekte” d av C-dur synges igjen.
Hvis dette ikke blir observert, faller du i kommafellen, som vist i følgende lydeksempel. Etter å ha gjentatt det fire ganger, høres settet nesten en halv tone lavere ut. Gjentagelse av komma-fellen fire ganger resulterer i en detonasjon av nesten en halvtone
| Tonic | , e | G | c | |
| Underdominant | f | , a | c | |
| Subdominant parallell | f | , a | , d | |
| Dominerende | , G | ,, H | , d | Med det samme er d av sopranen et (syntonisk) komma for dypt |
| Tonic | ,, e | , G | , c | Ett poeng for dypt |
| Underdominant | , f | ,, a | , c | Ett poeng for dypt |
| Subdominant parallell | , f | ,, a | ,, d | Ett poeng for dypt |
| Dominerende | ,, G | ,,, H | ,, d | Med samme ,, d av sopranen nå to kommaer for dype |
| Tonic | ,,, e | ,, G | ,, c | To kommaer for dype |
| Underdominant | ,, f | ,,, a | ,, c | To kommaer for dype |
| Subdominant parallell | ,, f | ,,, a | ,,, d | To kommaer for dype |
| Dominerende | ,,, G | ,,,, H | ,,, d | Med den samme ,,, d av sopranen nå tre komma for lavt |
| Tonic | ,,,, e | ,,, G | ,,, c | Tre kommaer for dype |
| Underdominant | ,,, f | ,,,, a | ,,, c | Tre kommaer for dype |
| Subdominant parallell | ,,, f | ,,,, a | ,,,, d | Tre kommaer for dype |
| Dominerende | ,,,, G | ,,,,, H | ,,,, d | Med den samme ,,, d av sopranen nå fire kommaer for dype |
| Tonic | ,,,,, e | ,,,, G | ,,,, c | Fire komma (86 cent ) for dyp |
Den kvintsirkel i Eulers leire nettet
To toner skifter til neste tast. Den kromatiske halvtonen med 92,179 cent (frekvensforhold: 135 ⁄ 128 ) kan sees på notatbildet , endringen med et syntonsett komma med 21,506 cent (frekvensforhold 81 ⁄ 80 ) kan leses fra de endrede centene.
De ♯ nøklene i Eulers tone nettverk
( Cent- verdier i parentes)
- C dur: c (0) d (204), e (386) f (498) g (702), a (884), h (1088) c
- G dur: ga (906), hcd, e, f skarp (590) g
- D dur: de (408), f skarp ga, b, c skarp (92) d
- En dur: ah (1110), c skarp de, f skarp, g skarp (794) a
- E dur: e f skarp (612), g skarp ah, c skarp, d skarp (296) e
- B dur: b c skarp (114), dis e f skarp, g skarp, en skarp (998) h
- FIS dur: f skarp g skarp (816), en skarp b c skarp, dis, is (500) f skarp
- CIS major: cis dis (318), ice fis gis, ais, his (2) cis
De ♭ nøklene i Eulers tone nettverk ( cent verdier i parentes)
- C dur: c (0) d (204), e (386) f (498) g (702), a (884), h (1088) c
- F dur: fg, fra (996) c, d (182), ef
- B-dur: bc, d es (294) f, g (680), ab
- Eb dur: es f, g as (792) b, c (-22), d es
- En flat dur: som b, c des (90) es, f (477), g som
- D-dur: des es, f ges (588) a flat, b (975), c des
- G-dur: ges as, b ces (1086) des, es (273), f tot
- C-dur: ces des, es fes (384) gb, en flat (771), b ces
Andreas Werckmeister slo allerede fast at enharmonisk ligning er mulig hvis man ser bort fra avviket med et skisma (<2 cent). Han forsømte dette intervallet på mindre enn 2 cent fordi det gjør "knapt en sirkelstrek" på monokordet:
- , h (1088) = ces (1086)
- , hans (2) = c (0)
- , cis (92) = des (90)
- , dis (296) = es (294)
- , e (386) = fes (384)
- , is (500) = f (498)
- , f skarp (590) = totalt (588)
- , g skarp (794) = en flat (792)
- , ais (998) = b (996)
litteratur
- Euler, Leonhard . I: Musikk i fortid og nåtid , bind 3, 1616
- Hermann von Helmholtz : Teorien om tonefølelser som et fysiologisk grunnlag for teorien om musikk. Vieweg, Braunschweig 1863 (opptrykk: Minerva-Verlag, Frankfurt am Main 1981, ISBN 3-8102-0715-2 , utdrag ).
- Ludwig Riemann: Populær representasjon av akustikk i forhold til musikk. Etter Hermann von Helmholtzs "Theory of Sound Sensations". Vieweg, Braunschweig 1896.
Se også
- Rent humør
- Ren tuning med keyboardinstrumenter
- Tonestruktur (matematisk beskrivelse)
- Modulering med ren innstilling
- Tonic sol-fa , der også rapporten av Hermann von Helmholtz, en talsmann for ren innstilling
- Vogels Tonnetz , en utvidelse av Eulers Tonnetz med syvendedeler
weblenker
- Joachim Mohr: Euler-stavemåten .
- Prøv det på PC-tastaturet. Gratis Java-applet
Individuelle bevis
- ↑ Leonhard Euler: Tentamen novae theoriae musicae ex certissimis harmoniae principiis dilucide expositae. St. Petersburg 1739.
- ^ Leonhard Euler: De harmoniae veris principiis per speculum musicum repraesentatis. I: Novi Commentarii academiae scientiarum Petropolitanae , 18, St. Petersburg 1774.
- ↑ Walter Odington
- ^ Harvard-ordboken for musikk. Don Michael Randel, 2003, ISBN 0-674-01163-5 , s. 56, overskrift: Aritmetisk og harmonisk gjennomsnitt, seksjon 2 ( online ).
- ↑ Følgende betegnelse brukes ofte: ("understreket x") i stedet for ("dypt komma x") og ("overstreket x") i stedet for 'x ("apostrof x")
- ↑ Jacques Handschin: Tonekarakteren . En introduksjon til tonepsykologi. Zürich 1948.
- ↑ Carl Dahlhaus : Undersøkelser av opprinnelsen til harmonisk tonalitet . Kassel 1965. Renate Imig: Systemer for funksjonell betegnelse i harmoniundervisning siden Hugo Riemann . Düsseldorf 1970.
- ↑ Moritz Hauptmann: Naturen til harmoni og beregninger. Leipzig 1853.
- ↑ Hermann v. Helmholtz: Teorien om tonefølelser som et fysiologisk grunnlag for teorien om musikk. Brunswick 1863.
- ^ Arthur von Oettingen: Harmoniesystem i dobbel utvikling. Studier på teorien om musikk. Dorpat / Leipzig 1866; Revidert andre utgave som Das duale Harmoniesystem , Leipzig 1913.
- ↑ z. B.: Hugo Riemann: Ideer for en ”doktrine om lydideer”. I: Jahrbuch Peters 21/22, 1914/15
- ↑ Martin Vogel: Teorien om toneforholdene. Bonn - Bad Godesberg 1975, s. 103f.
- ↑ Ross W. Duffin: Hvordan Equal Temperament Ødela Harmony (og hvorfor du bør Care). WW Norton & Company, New York NY 2007, ISBN 978-0-393-06227-4 ( utdrag ).
-
↑ For eksperten beregningen av frekvensene med c '= 264 Hz:
,, g skarp ' = Hz = 422,4 Hz, 'som' = Hz = 412,5 Hz, beregning med oktav = 1200 · lb (2), femte = 1200 lb ( 3 ⁄ 2 ), komma = 81 lb / 8o ) og c = 0 cent: ,, g skarpe = 8 femtedeler - 4 oktaver - 2 desimaltegn = 772.627 cent, 'som = −4 femtedeler + 3 oktaver + komma = 813.686 øre, forskjell = som ′ - ,, gis = 41.059 øre
- ↑ Bettina Gratzki s. 76: Den rene intonasjonen i korsang (= Orpheus publikasjonsserie om grunnleggende spørsmål i musikk 70). Forlaget for systematisk musikkvitenskap GmbH, Bonn 1993, ISBN 3-922626-70-X ( Utdrag ( minnesmerke av den opprinnelige fra 19 februar 2014 i Internet Archive ) Omtale: The arkiv koblingen er satt inn automatisk og har ennå ikke blitt sjekket . Sjekk original- og arkivlenken i henhold til instruksjonene, og fjern deretter denne meldingen. ).
- ↑ Med q = 701.955 (femte) og t = 386.314 (tredje) beregnes følgende (modulo oktav = 1200): c = 0, g = q, d = 2q, a = 3q, e = 4q osv. F = - q, b = −2q, es = −3q osv. Med s = 21.506 (syntonisk komma) :, c = c - s ,, g = g - s ,, d = d - s, ..., f = f - s ,, b =, b - s ,, es = es −s etc.
- Werk Andreas Werkmeister: Musikalsk temperatur. Quedlinburg 1691.












