Divisjon (matematikk)

${\ displaystyle 20: 4 = 5}$

Den Division er en av de fire aritmetiske basisoperasjoner av aritmetikk . Det er det motsatte av multiplikasjon . Inndelingen er også kjent som delt . Et utbytte deles med en divisor , resultatet kalles kvotienten . Den lange divisjonen er metoden for deling med penn og papir. Det undervises i barneskoleleksjoner . Det aritmetiske symbolet for divisjonen er , eller (delt symbol ). ${\ displaystyle:}$${\ displaystyle \ div}$${\ displaystyle /}$

definisjon

For å kunne diskutere inndeling som den velkjente grunnleggende aritmetiske beregningen, trenger man en matematisk struktur som kjenner to lenker (aritmetiske operasjoner), kalt addisjon og multiplikasjon. De to koblingene samhandler med hverandre i henhold til reglene for den matematiske ringen . Multiplikasjonen definerer divisjonen som den inverse operasjonen assosiert med den. Tillegg kreves som en ekstra grunnleggende aritmetisk funksjon, fordi den for eksempel definerer null (0) som det nøytrale elementet som tilhører den .

kommentar

I den kjente fra skolen er matematiske strukturer av heltallene av de rasjonelle tallene av reelle tall og de komplekse tallene matematiske ringer.${\ displaystyle \ mathbb {Z},}$${\ displaystyle \ mathbb {Q},}$ ${\ displaystyle \ mathbb {R}}$ ${\ displaystyle \ mathbb {C}}$

Deler eller deling betyr til et gitt tall (den kjente faktoren for) et passende tall (den ukjente faktoren) å finne, slik at multiplikasjonen av et ønsket produkt gir: finn, for et gitt og en slik at . ${\ displaystyle b}$${\ displaystyle x}$ ${\ displaystyle a}$${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle x}$${\ displaystyle b \ cdot x = a}$

Hvis du begrenser deg til hele tall , er dette ikke alltid mulig (se delbarhet ). ${\ displaystyle \ mathbb {Z}}$

I legemer , for eksempel i kroppen av rasjonelle tall eller i kroppene med reelle tall og komplekse tall , gjelder følgende: ${\ displaystyle \ mathbb {Q}}$${\ displaystyle \ mathbb {R}}$${\ displaystyle \ mathbb {C}}$

For hvert tall og for hvert tall som ikke er null , er det nøyaktig ett tall som tilfredsstiller ligningen .${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle x}$${\ displaystyle b \ cdot x = a}$

Inndelingen er derfor motsatt av multiplikasjonen for å bestemme dette . Man skriver ${\ displaystyle x}$

Følgende kalles:

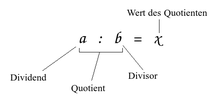
• Tallet som er delt, "utbytte" ( latin for " å dele" (nemlig: tall)), i brøker også "teller" .${\ displaystyle a}$
• Tallet som man deler med , "divisor" eller "divisor" ( latin for "den som deler"), kalte også nevneren i brøker .${\ displaystyle b}$
• Begrepet kalles " kvotient ".${\ displaystyle a: b}$
• Resultatet av inndelingen kalles "verdien av kvotienten" eller kvotientverdien , ofte også for kort .

Minnehjelpemidler:

• Utbytte etter divisor er lik verdien av kvotienten.
• Utbytte: Divisor = verdien av kvotienten ( eselbro : utbytte kommer før divisor i alfabetet )

eiendommer

Verken kommutativ lov eller assosierende lov gjelder splittelse . Imidlertid kan den spores tilbake til multiplikasjon fordi den holder

${\ displaystyle a: b = a \ cdot {\ tfrac {1} {b}} = a \ cdot b ^ {- 1}}$.

Det kan derfor være fordelaktig å skrive divisjonen som en multiplikasjon med den gjensidige verdien , siden multiplikasjonen er både assosiativ og kommutativ og dermed tillater enklere og mindre feilutsatt omforming. For delingen gjelder imidlertid den andre fordelingsloven med tillegg og subtraksjon , det vil si

${\ displaystyle (a + b): c = a: c + b: c}$og .${\ displaystyle (ab): c = a: cb: c}$

Man snakker her om divisjonens juridiske distribusjon. Imidlertid er den første fordelingsloven (venstre fordelingsevne) generelt ikke fornøyd med addisjon og subtraksjon.

Aritmetisk divisjon med null er ikke mulig

eksempel

Eksempel fra konditori: Hvis du vil dele en kake mellom null personer, hvor mye av kaken får hver person?

Det er ikke mulig å svare på spørsmålet, da det ikke er noen som får tak i kaken. Hvis du oversetter dette spørsmålet til matematikkens språk og abstrakte fra alle mulige ekstra-matematiske betydninger, blir det klare spørsmålet "Hvordan fordeler jeg noe til 0 steder?" Det rent matematiske problemet "Hvordan deler jeg med 0?".

Matematisk bevis

La være en ring med null element . I tilfelle "divisjon med null" blir den kjente faktoren (divisor) derfor spurt: ${\ displaystyle R}$${\ displaystyle 0}$
${\ displaystyle b = 0,}$

Er det en løsning på ligningen for et element ?${\ displaystyle a \ in R}$${\ displaystyle x \ i R}$${\ displaystyle 0 \ cdot x = a \}$

Dersom den null ringen , det vil si består av den eneste element 0, vil likning har løsningen fordi det er fordi det er ikke noe annet, og således etter behov. Dessuten er den eneste løsningen. ${\ displaystyle R}$${\ displaystyle R}$${\ displaystyle x = 0,}$${\ displaystyle a = 0,}$${\ displaystyle 0 \ ganger x = 0 \ ganger 0 = 0 = a,}$${\ displaystyle x = 0}$

I det følgende antas det generelt at det har minst 2 forskjellige elementer, noe som for eksempel per definisjon er tilfelle med et legeme . ${\ displaystyle R}$

Vi ser etter løsninger på ligningen for et ringelement . ${\ displaystyle a \ in R}$${\ displaystyle x}$${\ displaystyle 0 \ cdot x = a}$

• Sak 1 ::${\ displaystyle a \ neq 0}$

For et ringmedlem er ikke ligningen løselig , ikke i og ikke i en forlengelsesring . Fordi, som vist i artikkelen Ring (Algebra) , følger det av ringaksiomene , i stor grad distribusjonsloven : ${\ displaystyle a \ neq 0}$${\ displaystyle R}$ ${\ displaystyle S \ supset R}$

Det nøytrale elementet for tilsetning av en ring er en

annulator med for hvert ringelement .${\ displaystyle 0}$${\ displaystyle S}$${\ displaystyle 0 \ cdot x = 0}$${\ displaystyle x \ i S}$

• Sak 2 ::${\ displaystyle a = 0}$

Selv om ovenstående ligning løser hvert ringelement i saken , vil det å spesifisere en bestemt av dem ("gjøre divisjonen unik") føre til problemer. Når du for eksempel bosetter deg, velger du et ringelement . (Dette er mulig fordi den har minst to elementer.) Multiplikasjonens assosiative lov vil resultere i: ${\ displaystyle a = 0}$${\ displaystyle x \ i R}$${\ displaystyle x = 0: 0 = 1}$${\ displaystyle c \ neq 1}$${\ displaystyle R}$

${\ displaystyle 1 = 0: 0 = (c \ cdot 0): 0 = c \ cdot (0: 0) = c \ cdot 1 = c}$,

som ville motsette valget .${\ displaystyle c \ neq 1}$

Som et resultat betyr dette at størrelser som, når addisjon og multiplikasjon er tilstede , kjenner en "divisjon med null" i en hvilken som helst form ( uendelig , udefinert , NaN eller hva som helst ) ikke kan være ringer (enn si kropper) fordi ringegenskapene ikke kan kvotientene med divisor null - og er derfor ikke  gyldige for alle elementer . ${\ displaystyle M}$${\ displaystyle M}$${\ displaystyle M}$

Merknader

• Hvis ringen har null deler , for eksempel B. ringen av de resterende klasser modulo 6 Restbeløp , deretter ${\ displaystyle R: = \ mathbb {Z} / 6 \ mathbb {Z}}$ ${\ displaystyle 2,3,4 {\ text {mod}} 6}$
  1. ligningen kan ikke løses for alle . Eksempel: har ingen løsning i fordi den ikke inneholder resten .${\ displaystyle b \ cdot x = a}$${\ displaystyle b \ neq 0}$
     ${\ displaystyle 3 \ cdot x \ equiv 2 {\ text {mod}} 6}$${\ displaystyle R}$${\ displaystyle 3 \ cdot R \ equiv \ {0.3 \} {\ text {mod}} 6}$${\ displaystyle 2 {\ text {mod}} 6}$
  2. kan ha en ligning med flere løsninger. Eksempel: har de tre løsningene .${\ displaystyle b \ cdot x = a}$${\ displaystyle b \ neq 0}$
     ${\ displaystyle 3 \ cdot x \ equiv 3 {\ text {mod}} 6}$${\ displaystyle x \ equiv 1,3,5 {\ text {mod}} 6}$
• I den vitenskapelige matematiske litteraturen blir divisjon med null bare nevnt hvis dette er temaet i kapitlet.

Divisjon med null i datamaskinen

Spesielt når du spontant bruker en dataenhet, kan det skje at du deler med null . Målet med implementeringene er da,

1. å gjøre brukeren / programmereren oppmerksom på hendelsen og
2. å levere et (midlertidig) resultat som den mest lovende videre beregningen kan forventes med.

Fast punkt

En divisjon med null med faste punktnumre utløser en kjøretidsfeil (unntak) av divisjonen med nulltype ( nulldelings unntak ) på praktisk talt alle elektroniske databehandlingssystemer . En tilknyttet håndtering av dette unntaket spesifiseres og utføres vanligvis av kjøretidsmiljøet til det programmeringsspråket som brukes, men kan også spesifiseres mer detaljert av brukeren, for eksempel ved hjelp av en instruksjon. I noen kjøretider vil divisjon med null forårsake udefinert oppførsel .catch

Siden kjernen (i samarbeid med runtime-miljøet til programmeringsspråket) gir feilhåndterings-runtime-miljøet, kan en divisjon med null i selve kjernen føre til at hele datamaskinen krasjer .

Flytende punkt

Hvis et "overløp" oppstår under en flytende punktoperasjon , vil jeg. H. resultatet er for stort når det gjelder mengde til å vises hvis det er satt til et veldig stort flytpunkt med betydningen "uendelig" eller "minus uendelig". En flytende punkts divisjon med null blir også ofte behandlet på denne måten. B. fra den meget populære IEEE 754- standarden . Et flagg er også satt slik at det er mulig å programmere unntakshåndtering. (Artikkelen Permanence Principle diskuterer ulike begreper om hvordan en "divisjon med null" kunne defineres med minst mulig frafall av beregningsregler, f.eks. Ringaksiomer og ordrelasjoner.)

Er 1: 0 = ∞?

Graf av funksjonen .${\ displaystyle {\ tfrac {1} {x}}}$

Noen mennesker mener at løsningen med å dele på null må være uendelig , siden erfaring viser at individet blir mer og mer, jo færre er det som han må dele noe med. Men

1. for det første, ved å innføre en "verdi", blir ringstrukturen og dens aritmetikk - som vist ovenfor - forlatt. Mer vidtrekkende konsekvenser er de ubestemte uttrykkene som nå dukker opp (som uttrykkene av typen faktisk allerede tilhører og) som alle krever spesiell behandling.${\ displaystyle \ infty}$${\ displaystyle 1: 0}$
2. For det andre kommer et nytt matematisk konsept (som går utover aritmetikk, nemlig et topologisk ) inn i bildet gjennom metoden for grenseverdidannelse , som i noen tilfeller kan bestemmes et meningsfylt resultat for en oppgave som ikke kan beregnes direkte. Imidlertid, hvis du bruker denne metoden på eksemplet , strever resultatet faktisk mot uendelig, men bare hvis du nærmer deg null fra den positive siden, dvs. hvis du nærmer deg null fra retning av de negative tallene, så er verdien av funksjonen mot , så funksjonen på punktet strever mot så vel som mot , så den har ingen klar grenseverdi. Som eksemplet viser, er det flere problemer knyttet til strukturen og den viktige ordrelasjonen. Hvis du absolutt alltid vil tildele en verdi til divisjon (også til divisjon med null), så må dette også ha den unike egenskapen som ellers er vanlig for divisjon; en bestemmelse av en slik verdi er utilfredsstillende for hvert valg, og tildelingen av en løsningssettet er også utilfredsstillende .${\ displaystyle {\ tfrac {1} {x}}}$${\ displaystyle \ scriptstyle \ lim _ {x \ to 0 +} {\ tfrac {1} {x}} \; = \; + \ infty.}$${\ displaystyle - \ infty}$${\ displaystyle \ scriptstyle \ lim _ {x \ til 0 -} {\ tfrac {1} {x}} \; = \; - \ infty.}$${\ displaystyle x = 0}$${\ displaystyle + \ infty}$${\ displaystyle - \ infty}$
   ${\ displaystyle \ mathbb {Q}}$${\ displaystyle \ mathbb {R}}$
   ${\ displaystyle \ {\ infty, - \ infty \}}$

Gjenoppta

1. Komplikasjonene knyttet til innføringen av en "verdi" for er i alle henseender (særlig begrensningen av regningens gyldighet, den resulterende inflasjonen av de nødvendige beregningsreglene, tvetydighet) mye mer ufordelaktig enn den enkle erkjennelsen av det enkle faktum at ligninger av typen ikke har noen løsning. Snarere oppstår det mange nye problemer som ikke kan behandles ordentlig med en slik beregning.${\ displaystyle 1: 0}$${\ displaystyle 0 \ cdot x = 1}$
   
2. Avhengig av den gitte tilfelle er det ofte mulig, sammen med fremgangsmåter for analyse av ytterligere med tilsetningen av informasjon, f.eks. Monoton og kontinuitet for å komme til en god løsning, en løsning som husker at bare fullstendig fjernet til en "dele med null".

Divisjon med resten

Når det gjelder hele tall, gjelder følgende: En inndeling kan bare utføres fullstendig hvis utbyttet er et integrert multiplum av deleren. Generelt er imidlertid inndelingen ikke helt gjennomførbar, det vil si at det er en rest.

Divisjonslover

Delbarhetsregler (0-10)

Med de følgende delingsreglene for delere fra 0 til 10 (formulert for desimalnotasjoner ) får du hele tallresultater.

• Du kan ikke dele med 0 . Også nevneren til en brøkdel, selv om den inneholder variabler, som f.eks B. i ligningen y = 1 / x , må ikke resultere i 0. Hvis du deler 0 med et hvilket som helst tall (≠ 0), blir resultatet igjen 0 ( 0: x = 0; x ≠ 0 ). For divisjon 0: 0 er ikke noe resultat definert .
• Et vilkårlig tall annet enn 0 av seg selv oppdelt gi 1 ( x: x = 1, x ≠ 0) .
• Når du deler primtall , får du bare heltallverdier hvis du deler primtalet med seg selv (resulterer i 1) eller med 1 (resulterer i startnummer).
• Hvert tall kan deles med 1 . Denne inndelingen endrer ikke verdien ( x: 1 = x ).
• Hvert partall (siste siffer er 2, 4, 6, 8 eller 0) er delbart med 2 .
• Et tall kan deles med 3 hvis summen er delelig med 3.
• Et tall kan deles med 4 hvis de to siste sifrene er delbare med 4.
• Et tall kan deles med 5 hvis det siste sifferet er 5 eller 0.
• Et tall kan deles med 6 hvis det er jevnt og kontrollsummen er delelig med 3.
• Den deleligheten med 7 er et spesielt tilfelle der det er forskjellige regler.
• Et tall kan deles med 8 hvis de tre siste sifrene er delbare med 8.
• Et tall kan deles med 9 hvis summen er delelig med 9.
• Et tall kan deles med 10 hvis det siste sifferet er 0.

skilt

• Hvis utbyttet og divisoren har samme tegn, er kvotienten positiv.
• Hvis utbyttet og deleren har forskjellige tegn, er kvotienten negativ.

Disse to reglene gjelder mutatis mutandis for multiplikasjon .

Aritmetiske operasjoner

• Når du beregner et komplekst begrep, gjelder regelen " parentes før punktum før bindestrek ".

• To brøker deles av hverandre ved å multiplisere den første brøk med den gjensidige av den andre brøk (nevneren til en brøk kan ikke legge opp til 0):

(a / b): (c / d) = (a / b) * (d / c)

Om nødvendig må resultatet forkortes.

• I en ulikhet snur ulikhetstegnet når man deler (eller multipliserer med) et negativt tall, f.eks. B.

-2x < -10 |: (-2)

x > 5

Skrivemåter

Det er flere måter å skrive divisjonen på: eller eller eller${\ displaystyle a: b}$${\ displaystyle a \ div b}$${\ displaystyle a / b}$${\ displaystyle {\ frac {a} {b}}}$

Tykktarmen som et symbol for splittelse har bare vært i vanlig bruk siden Leibniz (1646–1716), selv om den også er kjent i eldre skrifter. William Oughtred introduserte notasjonen i sin Clavis Mathematicae fra 1631.

Notasjonen kalles også brøkrepresentasjon eller for brøkdel . Brøknotasjon er bare unik med kommutativ multiplikasjon; dette spiller en rolle i mer generelle matematiske strukturer, som nevnt nedenfor under "Generalisering". ${\ displaystyle {\ frac {a} {b}}}$

Hvis det er flere påfølgende kolon i en linje, blir ordren vanligvis behandlet fra venstre til høyre; infix kolonoperatoren er derfor venstreassosiativ :

${\ displaystyle a: b: c = (a: b): c = a \ cdot b ^ {- 1} \ cdot c ^ {- 1} = a: (b \ cdot c)}$.

generalisering

I abstrakt algebra som definerer algebraiske strukturer , kalles kroppen . Kropper er preget av det faktum at deling (unntatt 0) alltid er mulig i dem. Inndelingen skjer her ved å multiplisere med det inverse elementet i deleren.

I mer generelle strukturer (med ikke-kommutativ multiplikasjon) må det skilles mellom venstre divisjon og høyre divisjon. Assosiativ lovens (ikke-) gyldighet har også innvirkning på kvotientenes egenskaper.

Landsspesifikk

I Østerrike skilles det noen ganger mellom messer (hvor ofte går det inn ...?) Og deler (hvor mye resulterer det i delt på ...?)

Fram til 1970-tallet ble det tidvis skilt mellom å dele (i grupper) (østerrikske messer ) og distribuere i tyske grunnskoler .

Se også

• Gruppeteori
• Ringteori
• Skrå kropp
• Divisjonsalgebra
• Polynomial divisjon
• Rasjonell funksjon - funksjonsdeling
• Vedisk matematikk - Forenklet delingsmetode
• Kva-gruppe
• Ubestemt uttrykk (matematikk)

litteratur

• SA Stepanov: Divisjon . I: Michiel Hazewinkel (red.): Encyclopedia of Mathematics . Springer-Verlag og EMS Press, Berlin 2002, ISBN 978-1-55608-010-4 (engelsk, online ). 

weblenker

Wiktionary: Divisjon  - forklaringer på betydninger, ordets opprinnelse, synonymer, oversettelser

Individuelle bevis

1. ↑ Det er å foretrekke å notasjonen med en brøkstrek, særlig i den ikke-kommutativ tilfelle , fordi den angir en klar sekvens av operasjoner.${\ displaystyle {\ tfrac {a} {b}}}$
2. ↑ "Ikke løselig" er en skarpere uttalelse enn "udefinert". Når det gjelder sistnevnte, kan det fremdeles være en viss frihet for en definisjon. Med førstnevnte er denne muligheten ekskludert.
3. ↑ En reell grenseverdidannelse , for eksempel på samme måte som de l'Hospitals regel , er ikke å anse som divisjon med null.
4. ↑ ^{a b} Artikkelen Utvidet reelt tall bringer to topologiske utvidelser av de reelle tallene, men tar også for seg aritmetiske problemer.
5. ^ Senket av Windows NT . I: Wired News , 24. juli 1998. 
6. ↑ Python-feil og unntak. Hentet 30. mai 2017 . 
7. ↑ Java ArithmeticException. Hentet 30. mai 2017 . 
8. ↑ ISO / IEC 9899: 201x. (PDF; 1,6 MB) Hentet 30. mai 2017 (engelsk, ikke-normativt arbeidsdokument). 
9. ^ Eric Weisstein , Wolfram MathWorld : Divisjon med null
10. ^ Rochester Institute of Technology : Operasjonsrekkefølge
11. ^ Education Place: The Order of Operations
12. ↑ Khan Academy : The Order of Operations ( Video, fra 05:40 am )
13. ^ Virginia Department of Education : Using Order of Operations and Exploring Properties , avsnitt 9
14. ↑ Chemnitz University of Technology : Forrangsregler og assosiativitet
15. ↑ veritas.at