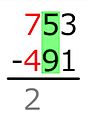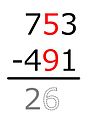subtraksjon

Den subtraksjon (av lat. Subtrahere "pull", "Fjern"), i dagligtale minus beregning kalles, er en av de fire aritmetiske basisoperasjoner av aritmetikk . Under subtraksjonen betyr fjerning av et tall av et annet. Matematisk er subtraksjonen en tosifret kombinasjon . Subtraksjonen er den motsatte av den tilsetning . Det aritmetiske symbolet for subtraksjonen er minustegnet "-".

Språkbestemmelser, grunnleggende egenskaper og notasjon

Følgende symboler og måter å snakke på brukes for elementene i en subtraksjon:

• Det aritmetiske symbolet for subtraksjonen er minustegnet "-". Den ble introdusert av Johannes Widmann i 1489 .
• Antallet noe trekkes fra kalles minuend (latin for "den som skal reduseres").
• Tallet som trekkes fra kalles subtrahend (latin for "egenandelen").
• Det aritmetiske uttrykket ( begrepet ) som inkluderer minuend, minustegn og subtrahend kalles forskjellen .
• Resultatet av en subtraksjon er verdien av forskjellen (også forskjell eller bare forskjell ).
• Symbolet for forskjeller som termer er den greske hovedbokstaven delta "Δ", som også brukes som en operator for forskjellsdannelse (se nedenfor). Ofte forskjell - særlig i daglig bruk - er bare det resultat av denne "minus beregning", og oftere mengden av dette resultatet. Eksempel: Forskjellen mellom 7 og 9 og forskjellen mellom 5 og 3 er 2 . I eksemplet blir dette understreket av verbet "beløp".

Mnemonic: minuend minus subtrahend lik verdi av forskjellen ( Mnemonic : M inuend kommer i alfabetet før S ubtrahend)

Eksempler (med tanke på tegnet!):

• 4 minus 1 er skrevet (det samme) 3 eller annerledes .${\ displaystyle 4-1 = 3}$

4 er minuend, 1 er subtrahend, det aritmetiske uttrykket (begrepet) er forskjellen og resultatet 3 er verdien av differansen eller differensverdien. ${\ displaystyle 4-1}$

Settet med naturlige tall er ikke komplett med hensyn til subtraksjon , det vil si at med subtraksjon oppnår man muligens et resultat som overstiger området for naturlige tall .

• Eksempel: ${\ displaystyle 1-4 = -3}$

Det er forkortede notasjoner for for eksempel, eller , som hovedsakelig brukes til begreper som eller . ${\ displaystyle fra}$${\ displaystyle x | _ {x = b} ^ {x = a}}$${\ displaystyle [x] _ {b} ^ {a}}$${\ displaystyle f (a) -f (b) = f (x) | _ {x = b} ^ {x = a}}$${\ displaystyle F (a) -F (b) = [F (x)] _ {b} ^ {a} = [F (x)] _ {x = b} ^ {x = a} = F (x ) {\ Big |} _ {b} ^ {a} = F (x) {\ Big |} _ {x = b} ^ {x = a}}$

Hvis flere subtraksjoner forekommer etter hverandre, behandles uttrykket fra venstre til høyre; subtraksjonen er derfor venstreassosiativ :

• ${\ displaystyle abc = (ab) -c}$.

Matematisk definisjon

Subtraksjonen er den motsatte av den tilsetning . I grupper kan du finne nøyaktig en for hver gitt, og slik at: ${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle x}$

${\ displaystyle b + x = a \!}$

Bestemmelsen av kalles subtraksjon . kan bestemmes ved å trekke fra : ${\ displaystyle x}$${\ displaystyle x}$${\ displaystyle b}$${\ displaystyle a}$

${\ displaystyle x = fra}$

${\ displaystyle a}$kalles minuend , den subtrahend . Resultatet av en subtraksjon, her , kalles verdien av forskjellen . En subtraksjon er notert med minustegnet: ${\ displaystyle b}$${\ displaystyle x}$

${\ displaystyle fra}$

Subtraksjonen kan også defineres som å legge til motsatt antall subtrahend til minuend : ${\ displaystyle fra}$ ${\ displaystyle -b = (- 1) \ cdot b}$${\ displaystyle a}$

${\ displaystyle ab = a + (- 1) \ cdot b = a + (- b)}$

Grunnleggende prosedyre

Grafisk metode

I den grafiske metoden er de numeriske verdiene representert som søyler, linjer, punkter eller andre abstrakte objekter. En annen mulighet er representasjonen med vektorer , hvor retning av subtrahendvektoren blir reversert og vektorene blir deretter lagt sammen.

eksempel

•

•

•

•

•

•

•

•

•

•

•

•

•

(1. 3)

-

•

•

•

•

•

•

•

•

•

(9)

=

•

•

•

•

(4)

Subtraksjon-subtraksjonsmetode

Med subtraksjon-subtraksjonsmetoden trekkes en delvis mengde av subtrahend fra subtrahend og minuend til subtrahend er 0. En tiere blir vanligvis valgt som et mellomtrinn.

eksempel

${\ displaystyle 13-9 = (13-3) - (9-3) = 10-6 = 4}$

Subtraksjon-tilleggsmetode

Med subtraksjon-addisjonsmetoden blir subtrahend og minuend brutt ned i underkomponenter, trukket fra disse, og deretter blir delmengdene lagt opp igjen.

eksempel

${\ displaystyle 13-9 = (10 + 3) -9 = (10-9) + 3 = 1 + 3 = 4}$

Utfyllingsmetode

Med komplementmetoden beregnes det tilsvarende komplementet fra subtrahend . Deretter blir minuend og komplement av subtrahend lagt til. Metoden er spesielt innen teknisk datalogi , som i det mekaniske feltet Tarrant- Comptometer , det mekaniske Hoffritz-huggeren og elektroniske tilsetningsstoffer i moderne datasystemer.

eksempel

Startformel:

${\ displaystyle 13_ {10} -9_ {10} = 1101_ {2} -1001_ {2}}$

Dette samsvarer med:

${\ displaystyle 13_ {10} + \ left (-9_ {10} \ right) = 1101_ {2} + \ left (-1001_ {2} \ right)}$

Beregning av komplementet:

Beregning av komplementet

kirurgi	Resultatverdi
	Titalls komplement	To komplement
Grunnlinje	${\ displaystyle \ ldots \ 000 \ 009,0_ {10}}$	${\ displaystyle \ ldots \ 0000 \ 1001,0_ {2}}$
Inversjon	${\ displaystyle \ ldots \ 999 \ 990, {\ dot {9}} _ {10}}$	${\ displaystyle \ ldots \ 1111 \ 0110, {\ dot {1}} _ {2}}$
Med ${\ displaystyle 0, {\ dot {9}} _ {10} = 0, {\ dot {1}} _ {2} = 1}$	${\ displaystyle \ ldots \ 999 \ 991,0_ {10}}$	${\ displaystyle \ ldots \ 1111 \ 0111,0_ {2}}$

Addisjon:

${\ displaystyle {\ begin {array} {rrrcrrr} & 13_ {10} &&& 1101_ {2} \\ + & \ ldots \ 999 \ 991_ {10} && + & \ ldots \ 1111 \ 0111_ {2} \\ = & 4_ {10} && = & 100_ {2} \ end {array}}}$

Skriftlig subtraksjon

I tillegg til skriftlig tillegg er skriftlig subtraksjon en av de grunnleggende kulturteknikkene som læres de første årene på grunnskolen. Å mestre den skriftlige subtraksjonen er en forutsetning for å lære den skriftlige inndelingen .

Vertikal subtraksjon med overføres

I barneskoler i dag læres det oftest prosedyrer der de tilsvarende posisjonene til minuend og subtrahend er oppå hverandre . Stillingene behandles etter hverandre, for det meste fra høyre til venstre.

For skriftlig subtraksjon må minuend (nummer over) være større enn eller lik subtrahend (nummer (er) nedenfor). Negative resultater er derfor ikke mulig direkte.

Hvis minuend er mindre enn subtrahend, kan skiltene byttes ut for beregningen. Subtraend blir minuend (skrevet ovenfor) og minuend blir subtrahend (skrevet nedenfor). Fremgangsmåten beskrevet nedenfor kan deretter brukes til beregning. På slutten må imidlertid resultatet tilføres et minus, fordi det alltid er negativt (ikke et naturlig tall). Dette reverserer skiltendringen som tidligere ble utført for beregningen.

Hvis sifferet i subtrahend er større enn de samme stedene de minuend behovet overføringer håndteres. Det vil si at minuend økes med 10 for å muliggjøre subtraksjon; For å kompensere for dette, må enten minuend reduseres i kolonnen ved siden av venstre (adskillelsesprosedyre; forhåndsberegning av overføringene) eller subtrahend må økes (tilleggsprosedyre, subtraksjon fra høyre til venstre). I det tyskspråklige området har sistnevnte tilnærming gått frem med den supplerende prosedyren. I 2000 trådte en ny læreplan i kraft i noen føderale stater , som nå foreskriver utbinding som standard i stedet for å supplere den.

Supplerende prosedyre

Med den supplerende metoden , som også kalles fylleteknikken eller (i USA) den østerrikske metoden ("østerriksk metode"), blir det ikke foretatt noen subtraksjon, men subtraend økes til slutten av minuttet . Hvis dette ikke er mulig, økes minuend med 10. 10 er ikke "lånt", men legges til som 1 i trekk fra neste delberegning. I tysktalende land læres denne prosedyren som en standardmetode i grunnskoler. En av fordelene med metoden er at den forbereder håndteringen av oppgaver der flere subtrahender skal trekkes fra et minuend.

eksempel

	beskrivelse
${\ displaystyle {\ begin {array} {r} 75 {\ color {red} 3} \\ - {\ underset {} {4}} 9 {\ color {red} 1} \\\ hline \ end {array }}}$	1 +… = 3
${\ displaystyle {\ begin {array} {r} 7 {\ color {red} 5} 3 \\ - {\ underset {} {4}} {\ color {red} 9} 1 \\\ hline {\ color {Grå} 2} \ end {array}}}$	Resultatet er skrevet under linjen.
${\ displaystyle {\ begin {array} {r} 7 {\ color {red} 5} 3 \\ - {\ underset {} {4}} {\ color {red} 9} 1 \\\ hline {\ color {Grå} 2} \ end {array}}}$	9 +… = 5 Målsummen (5) er for liten!
${\ displaystyle {\ begin {array} {r} 7 {\ color {red} 5} 3 \\ - {\ underset {\ color {red} 1} {4}} {\ color {red} 9} 1 \ \\ hline {\ color {Grey} 2} \ end {array}}}$	Det økes derfor med 10. Den 1 er skrevet under neste subtrahend.
${\ displaystyle {\ begin {array} {r} 7 {\ color {red} 5} 3 \\ - {\ underset {\ color {red} 1} {4}} {\ color {red} 9} 1 \ \\ hline {\ color {Gray} 62} \ end {array}}}$	9 +… = 15 Beregningen kan nå utføres, resultatet skrives under linjen.
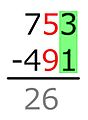
${\ displaystyle {\ begin {array} {r} {\ color {red} 7} 53 \\ - {\ color {red} {\ underset {1} {4}}} 91 \\\ hline {\ color { Grå} 62} \ end {array}}}$	(4 + 1) +… = 7
${\ displaystyle {\ begin {array} {r} {\ color {red} 7} 53 \\ - {\ color {red} {\ underset {1} {4}}} 91 \\\ hline {\ color { Grå} 262} \ end {array}}}$	Resultatet er skrevet under linjen.
${\ displaystyle {\ begin {array} {r} 753 \\ - {\ undersett {1} {4}} 91 \\\ hline {\ color {Grey} 262} \ end {array}}}$	Det samlede resultatet.

Subtraksjon fra venstre til høyre

Subtraksjonen kan også utføres fra venstre til høyre. I denne uvanlige prosedyren, som er en variant av den supplerende prosedyren, behandles overføringene før differansen beregnes nøyaktig. Siden overføringene verken må noteres eller huskes, er metoden ikke bare relativt motstandsdyktig mot uforsiktige feil, men også veldig rask og til og med egnet for mental aritmetikk.

eksempel

• 

  7 - 4 = 3
  Denne verdien er bare notert, ikke notert.

• 

  Siden minuend i den følgende kolonnen er mindre enn subtrahend, reduseres den nettopp beregnede verdien med 1.

• 

  15 - 9 = 6

• 

  Siden minuend i følgende kolonne ikke er mindre enn subtrahend, forblir denne verdien.

• 

  3 - 1 = 2

Hvis det er en kolonne eller en sekvens av flere kolonner der det er funnet to identiske sifre, og til høyre for den en kolonne med en minuend som er mindre enn subtrahend, gjør ikke rutinen "fremover" som brukes i denne prosessen trenger bare å ha de samme to sifrene, men inkluderer også følgende kolonner. Hver kolonne med de samme sifrene mottar deretter en ni i stedet for en null som et resultat.

Prognosen over flere kolonner i tilfellene beskrevet ovenfor er et svakt punkt i denne metoden.

Oppdeling av prosedyre

Tilbakekalling med ”adskillelse” betyr at den for lille Minuend gir et ”lån” med sin venstre nabo. Minuend økes med 10 og venstre nabo reduseres med 1. Prosessen brukes for eksempel i barneskoler. B. underviste i USA som standard praksis. Den rene databehandlingen ligner på den supplerende prosedyren; Men hvis et null må "lånes", må det "låne" fra sin egen venstre nabo - en teknikk som må læres i tillegg (det er ikke nødvendig i den supplerende prosedyren). Det må også skrives mer når det skilles.

eksempel

	beskrivelse
${\ displaystyle {\ begin {array} {r} 75 {\ color {red} 3} \\ - 49 {\ color {red} 1} \\\ hline \ end {array}}}$	3 - 1 = ...
${\ displaystyle {\ begin {array} {r} 75 {\ color {red} 3} \\ - 49 {\ color {red} 1} \\\ hline {\ color {Grey} 2} \ end {array} }}$	Resultatet er skrevet under linjen.
${\ displaystyle {\ begin {array} {r} 7 {\ color {red} 5} 3 \\ - 4 {\ color {red} 9} 1 \\\ hline {\ color {Grey} 2} \ end { array}}}$	5 - 9 =… Minuend (5) er for liten!
${\ displaystyle {\ begin {array} {r} {\ overset {\ color {Grå} 6} {\ avbryt {7}}} {\ oversett {\ color {rød} 15} {\ avbryt {5}}} 3 \\ - 4 {\ color {red} 9} 1 \\\ hline {\ color {Grey} 2} \ end {array}}}$	Det økes derfor med 10. Denne 10 er "lånt" fra nummeret (7) til venstre; dette reduseres med 1.
${\ displaystyle {\ begin {array} {r} {\ oversett {\ color {Grå} 6} {\ avbryt {7}}} {\ oversett {\ color {rød} 15} {\ avbryt {5}}} 3 \\ - 4 {\ color {red} 9} 1 \\\ hline {\ color {Grey} 62} \ end {array}}}$	15 - 9 =… Subtraksjonen kan nå utføres. Resultatet er skrevet under linjen.
${\ displaystyle {\ begin {array} {r} {\ overset {\ color {Red} 6} {\ cancel {7}}} {\ overset {\ color {Gray} 15} {\ cancel {5}}} 3 \\ - {\ color {red} 4} 91 \\\ hline {\ color {Gray} 62} \ end {array}}}$	6 - 4 = ...
${\ displaystyle {\ begin {array} {r} {\ overset {\ color {Red} 6} {\ cancel {7}}} {\ overset {\ color {Gray} 15} {\ cancel {5}}} 3 \\ - {\ color {red} 4} 91 \\\ hline {\ color {Grey} 262} \ end {array}}}$	Resultatet er skrevet under linjen.
${\ displaystyle {\ begin {array} {r} {\ overset {\ color {Grey} 6} {\ cancel {7}}} {\ overset {\ color {Gray} 15} {\ cancel {5}}} 3 \\ - 491 \\\ hline {\ color {Grey} 262} \ end {array}}}$	Det samlede resultatet.

Foroppbinding

En variant av adskillelsesprosessen er at alle punkter er fullstendig oppdelte i et første arbeidstrinn, slik at det er tilstrekkelig store minuender tilgjengelig for det andre arbeidstrinnet, der det bare trekkes fra.

eksempel

	beskrivelse
${\ displaystyle {\ begin {array} {r} 75 {\ color {red} 3} \\ - 49 {\ color {red} 1} \\\ hline \ end {array}}}$	3 - 1 = mulig. Ingen "lån" fra nummeret til venstre er nødvendig.
${\ textstyle {\ begin {array} {r} {\ overset {\ color {Grey} 6} {\ cancel {7}}} {\ overset {\ color {Gray} 15} {\ cancel {\ color {red } 5}}} 3 \\ - 4 {\ color {red} 9} 1 \\\ hline \ end {array}}}$	5 - 9 = ikke mulig. 5 økes med 10. Siden 10 er "lånt" fra 7 ved siden av den til venstre, må den reduseres med 1.
${\ displaystyle {\ begin {array} {r} {\ overset {\ color {Grey} 6} {\ cancel {7}}} {\ overset {\ color {Gray} 15} {\ cancel {5}}} {\ color {red} 3} \\ - 49 {\ color {red} 1} \\\ hline {\ color {Grey} 2} \ end {array}}}$	Behandling av sifrene: 3 - 1 = 2
${\ displaystyle {\ begin {array} {r} {\ oversett {\ color {Grå} 6} {\ avbryt {7}}} {\ oversett {\ color {rød} 15} {\ avbryt {5}}} 3 \\ - 4 {\ color {red} 9} 1 \\\ hline {\ color {Grey} 62} \ end {array}}}$	15 - 9 = 6
${\ displaystyle {\ begin {array} {r} {\ overset {\ color {red} 6} {\ cancel {7}}} {\ overset {\ color {Gray} 15} {\ cancel {5}}} 3 \\ - {\ color {red} 4} 91 \\\ hline {\ color {Grey} 262} \ end {array}}}$	6 - 4 = 2

Vertikal subtraksjon uten fremføringer

Delvise forskjeller

De Partielle Forskjeller metoden skiller seg fra andre vertikale subtraksjon metoder i at det ikke bruk bærer over. De erstattes av delvise forskjeller, som - avhengig av om minuend eller subtrahend er større i en kolonne - får et pluss- eller minustegn. Summen av de delvise forskjellene resulterer i den totale forskjellen.

eksempel

	beskrivelse
${\ displaystyle {\ begin {array} {rr} & {\ color {red} 7} 53 \\ - & {\ color {red} 4} 91 \\\ hline {\ color {Grey} +} & {\ farge {Grå} 300} \ end {array}}}$	Det mindre tallet trekkes fra det større: 700 - 400 = 300 Fordi minuend er større enn subtrahend, får forskjellen et pluss-tegn.
${\ displaystyle {\ begin {array} {rr} & 7 {\ color {red} 5} 3 \\ - & 4 {\ color {red} 9} 1 \\\ hline {\ color {Grey} +} & {\ color {Grey} 300} \\ {\ color {Grey} -} & {\ color {Grey} 40} \ end {array}}}$	Det mindre tallet trekkes fra det større: 90 - 50 = 40 Fordi subtrahend er større enn minuend, blir forskjellen gitt et minustegn.
${\ displaystyle {\ begin {array} {rr} & 75 {\ color {red} 3} \\ - & 49 {\ color {red} 1} \\\ hline {\ color {Grey} +} & {\ farge {Grå} 300} \\ {\ farge {Grå} -} og {\ farge {Grå} 40} \\ {\ farge {Grå} +} og {\ farge {Grå} 2} \ end {array}} }$	Det mindre tallet trekkes fra det større: 3 - 1 = 2 Fordi minuend er større enn subtrahend, får forskjellen et pluss-tegn.
${\ displaystyle {\ begin {array} {rr} & 753 \\ - & 491 \\\ hline {\ color {red} +} & {\ color {red} 300} \\ {\ color {red} -} & {\ color {red} 40} \\ {\ color {red} +} & {\ color {red} 2} \\\ hline & {\ color {Grey} 262} \ end {array}}}$	+ 300 - 40 + 2 = 262

Ikke-vertikale prosedyrer

Overdrift av forskjellen

Beregningen av en forskjell trenger ikke gjøres siffer for siffer. For det meste tungvint, men det er også mulig å gå gjennom tallområdet mellom en subtrahend og en minuend.

eksempel

1234 - 567 = kan beregnes ved hjelp av følgende trinn:

• 567 +  3  = 570
• 570 +  30  = 600
• 600 +  400  = 1000
• 1000 +  234  = 1234

For å bestemme forskjellen legges verdiene til de enkelte trinnene til: 3 + 30 + 400 + 234 = 667.

Nedbrytning av subtrahend

En annen tilnærming som er like egnet for skriftlig subtraksjon og mental aritmetikk er å bryte ned subtrahend, som trekkes fra minuend i individuelle trinn.

eksempel

"1234 - 567 =" kan beregnes ved hjelp av følgende trinn:

• 1234 -  500  = 734
• 734 -  60  = 674
• 674 -  7  = 667

Samme forandring

Den samme endringen subtrahering er basert på observasjonen at en subtraksjon er lett å utføre hvis det er en eller flere nuller på slutten av subtrahend. Med denne metoden økes eller reduseres subtrahend derfor til nærmeste ti; siden minuend økes eller reduseres med samme forskjell, har manipulasjonen ingen innflytelse på forskjellen. Hvis oppgaven fortsatt er for vanskelig etter det, kan operasjonen gjentas.

eksempel

"1234 - 567 =" kan beregnes ved hjelp av følgende trinn:

• 1234-567 = 1237-570 = 1267-600 = 667

weblenker

• Eksempler på stripping med adskillelse og utvidelsesteknologi (PDF-fil; 39 kB)
• Epler - Treningsprogram for gratisprogram for skriftlig subtraksjon

Individuelle bevis

1. ^ Rochester Institute of Technology : Operasjonsrekkefølge
2. ^ Education Place: The Order of Operations
3. ↑ Khan Academy : The Order of Operations ( Video, fra 05:40 am )
4. ^ Virginia Department of Education : Using Order of Operations and Exploring Properties , avsnitt 9
5. ↑ Chemnitz University of Technology : Forrangsregler og assosiativitet
6. ^ Donald E. Knuth: The Art of Computer Programming, Volume 2: Seminumerical Algorithms . 3. Utgave. Addison-Wesley, New York 1997, ISBN 978-0-201-89684-8 . 
7. ^ The Many Ways of Arithmetic in UCSMP Everyday Mathematics Subtraction: Trade First
8. ↑ Delvis-Forskjeller subtraksjon ( Memento av den opprinnelige fra 23 juni 2014 i Internet Archive ) Omtale: Den arkivet koblingen ble satt inn automatisk og har ennå ikke blitt sjekket. Vennligst sjekk originalen og arkivlenken i henhold til instruksjonene, og fjern deretter denne meldingen. ; The Many Ways of Arithmetic in UCSMP Everyday Mathematics Subtraction: Partial Differences @1@ 2Mal: Webachiv / IABot / ouronlineschools.org
9. ↑ The Many Ways of Arithmetic in UCSMP Everyday Mathematics Subtraction: Counting Up
10. ^ The Many Ways of Arithmetic in UCSMP Everyday Mathematics Subtraction: Left to Right Subtraction
11. ^ The Many Ways of Arithmetic in UCSMP Everyday Mathematics Subtraction: Same Change Rule