Lineær ligning

En lineær ligning er en matematisk bestemmelse av ligning hvor bare lineære kombinasjoner av de ukjente forekomme. Et kjennetegn ved en lineær ligning er at alle ukjente kun er til kraften til den første, dvs. det forekommer ikke, for eksempel i kvadrat (se kvadratisk ligning ). Vanligvis er ukjente av en lineær ligning skalarer , for det meste reelle tall . I det enkleste tilfellet av ukjent skalar , har en lineær ligning form ${\ displaystyle x}$

${\ displaystyle a \ cdot x = b}$,

hvor og er konstanter . Men det er også lineære ligninger med flere ukjente og med andre matematiske objekter som ukjente, for eksempel sekvenser ( lineære forskjellsligninger ), vektorer ( lineære ligningssystemer ) eller funksjoner ( lineære differensialligninger ). Generelt sett har en lineær ligning formen ${\ displaystyle a}$${\ displaystyle b}$

${\ displaystyle T (x) = b}$,

hvor er et lineært kart . ${\ displaystyle T}$

Homogene lineære ligninger er spesielle lineære ligninger der ligningens konstante begrep er null . Løsningene av en homogen lineær likning danner et underrom av den vektorrommet av det ukjente og således har spesielle egenskaper som gyldigheten av superposisjonsprinsippet . Løsningene til en inhomogen lineær ligning, derimot, danner et affint underområde , slik at hver løsning av en inhomogen lineær ligning kan representeres som summen av løsningen i den tilknyttede homogene ligningen og en partikkelformet løsning. Den løsning plass av en lineær ligning kan karakteriseres gjennom kjernen og den koks kjerne av den lineære kartlegging . ${\ displaystyle b}$

Lineære ligninger og deres løsninger studeres spesielt i lineær algebra og lineær funksjonsanalyse , men de spiller også en rolle i tallteorien .

Skalære lineære ligninger

Ofte er ukjente i lineære ligninger skalarer (for det meste reelle eller komplekse tall ). Slike lineære ligninger er da spesielle algebraiske ligninger av grad 1.

Lineære ligninger med en ukjent

En skalar ligning med en ukjent kalles lineært dersom det omdannes til form av ekvivalens transformasjoner (se løse ligninger ) ${\ displaystyle x}$

${\ displaystyle a \ cdot x = b}$

kan bringes. Hvor og er konstanter som ikke er avhengige av. ${\ displaystyle a}$${\ displaystyle b}$ ${\ displaystyle x}$

Er , verdien av det ukjente som ligningen er tilfreds med kan bestemmes ved å dele på begge sider av : ${\ displaystyle a \ neq 0}$${\ displaystyle x}$${\ displaystyle a}$

${\ displaystyle x = {\ frac {b} {a}}}$

Hvis og er, har ligningen ingen løsning. Hvis og er, er det uendelig mange løsninger, for da tilfredsstiller hver og en ligningen. ${\ displaystyle a = 0}$${\ displaystyle b \ neq 0}$${\ displaystyle a = 0}$${\ displaystyle b = 0}$${\ displaystyle x}$

Eksempler

Løsningen på den lineære ligningen

${\ displaystyle 3 \ cdot x = 24}$

oppnådd av begge sider med 3 delt slik at bare det ukjente på venstre side er igjen: ${\ displaystyle x}$

${\ displaystyle x = {\ frac {24} {3}} = 8}$.

Den lineære ligningen

${\ displaystyle 0 \ cdot x = 7}$

har ingen løsning mens den lineære ligningen

${\ displaystyle 0 \ cdot x = 0}$

for hver er oppfylt. ${\ displaystyle x}$

Lineære ligninger med to ukjente

Løsningssettet til den lineære ligningen ${\ displaystyle 3x + 4y = 12}$

En skalarligning med to ukjente og kalles lineær hvis den konverteres til formen ved ekvivalensomregninger ${\ displaystyle x}$${\ displaystyle y}$

${\ displaystyle a \ ganger x + b \ ganger y = c}$

kan bringes der , og er konstanter. Løsningene danner rette linjer i to-dimensjonale rommet , hvis ikke både og gjelder. Man snakker da om koordinatformen til en ligning med rett linje . Ellers er løsningssettet enten hele det todimensjonale rommet eller tomt . ${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle c}$${\ displaystyle a = 0}$${\ displaystyle b = 0}$${\ displaystyle (c = 0)}$${\ displaystyle (c \ neq 0)}$

Løsningen på en slik ligning er ofte gitt i parametrisk fremstilling . For å gjøre dette løser man ligningen for en av de ukjente, for eksempel hva, hvis , ${\ displaystyle y}$${\ displaystyle b \ neq 0}$

${\ displaystyle y = (ca \ cdot x) / b}$

og behandler den andre ukjente som en gratis parameter . Dette kan brukes som en ${\ displaystyle x}$${\ displaystyle t}$

${\ displaystyle x = t}$  og     med  ${\ displaystyle y = (ca \ cdot t) / b}$${\ displaystyle t \ in \ mathbb {R}}$

skrive. På denne måten blir det klart at selv om ligningen inneholder to ukjente, er løsningsrommet bare endimensjonalt, dvs. bare avhenger av en parameter . Den parametriske representasjonen i seg selv er ikke klar. Er , kan ligningen etter oppløsning og velge som gratis parametere. Andre parametreringer er også mulige, men de beskriver det samme settet med løsninger. ${\ displaystyle t}$${\ displaystyle a \ neq 0}$${\ displaystyle x}$${\ displaystyle y}$

eksempel

Løsningssettet for den lineære ligningen

${\ displaystyle 3 \ ganger x + 4 \ ganger y = 12}$

er ved å løse for som ${\ displaystyle y}$

${\ displaystyle x = t}$  og     med  ${\ displaystyle y = (12-3 \ cdot t) / 4}$${\ displaystyle t \ in \ mathbb {R}}$

gitt. Den funksjon graf av den rette linje som beskrives blir så oppnådd fra den rette linje ligning

${\ displaystyle f (x) = (12-3 \ cdot x) / 4 = - (3/4) \ cdot x + 3}$.

Lineære ligninger med flere ukjente

Løsningen på en ekte lineær ligning med tre ukjente er generelt et plan.

Generelt kalles en skalarligning med ukjente lineær hvis den konverteres til formen ved ekvivalente konverteringer ${\ displaystyle n}$${\ displaystyle x_ {1}, x_ {2}, \ dotsc, x_ {n}}$

${\ displaystyle a_ {1} x_ {1} + a_ {2} x_ {2} + \ dotsb + a_ {n} x_ {n} = b}$

kan bringes, hvor og er konstanter. Bare lineære kombinasjoner av ukjente tillater å forekomme. Løsningene til slike ligninger er generelt -dimensjonale undergrupper ( hyperplaner ) av det tilhørende -dimensjonale rommet. Hvis løsningssettet enten er hele dimensjonsområdet eller tomt . ${\ displaystyle a_ {1}, a_ {2}, \ dotsc, a_ {n}}$${\ displaystyle b}$${\ displaystyle (n-1)}$${\ displaystyle n}$${\ displaystyle a_ {1} = a_ {2} = \ dotsb = a_ {n} = 0}$${\ displaystyle n}$${\ displaystyle (b = 0)}$${\ displaystyle (b \ neq 0)}$

Den parametriske representasjonen av løsningssettet oppnås igjen i det generelle tilfellet ved å løse ligningen for en av de ukjente, for eksempel hvis , ${\ displaystyle x_ {n}}$${\ displaystyle a_ {n} \ neq 0}$

${\ displaystyle x_ {n} = (b-a_ {1} x_ {1} - \; \ cdots \; - a_ {n-1} x_ {n-1}) / a_ {n}}$,

og de andre ukjente som gratis parametere for å bli gravid. Løsningssettet er således gitt som ${\ displaystyle t_ {1}}$${\ displaystyle t_ {n-1}}$

${\ displaystyle x_ {1} = t_ {1}, \ dotsc, x_ {n-1} = t_ {n-1}, x_ {n} = (b-a_ {1} t_ {1} - \ dotsb - a_ {n-1} t_ {n-1}) / a_ {n}}$  med   .${\ displaystyle t_ {1}, \ dotsc, t_ {n-1} \ in \ mathbb {R}}$

Fordi parametere kan velges fritt, er løsningsområdet -dimensjonalt. Også her er parameterrepresentasjonen ikke entydig; ligningen kan også løses for en av de andre ukjente, forutsatt at den tilknyttede koeffisienten ikke er lik null, eller en annen parameterisering kan velges. ${\ displaystyle n-1}$${\ displaystyle (n-1)}$

eksempel

Løsningssettet til den lineære ligningen med tre ukjente

${\ displaystyle 3 \ cdot x_ {1} +2 \ cdot x_ {2} + x_ {3} = 7}$

er et plan i tredimensjonalt rom med representasjon

${\ displaystyle x_ {1} = t_ {1}, \; x_ {2} = t_ {2}, \; x_ {3} = 7-3 \ cdot t_ {1} -2 \ cdot t_ {2}}$  med   .${\ displaystyle t_ {1}, t_ {2} \ in \ mathbb {R}}$

Generelle lineære ligninger

Lineære kart

Generelt er lineære ligninger definert ved hjelp av lineære kart . En formligning

${\ displaystyle T (x) = b}$

kalles lineær hvis er en lineær kartlegging og hvis er uavhengig av . Kartleggingen kartlegges fra et vektorrom til et vektorrom , hvor og er. Begge vektorområdene er definert over en felles kropp . En kartlegging er lineær når det gjelder konstanter${\ displaystyle T}$${\ displaystyle b}$${\ displaystyle x}$${\ displaystyle T \ colon V \ to W}$ ${\ displaystyle V}$${\ displaystyle W}$${\ displaystyle x \ i V}$${\ displaystyle b \ in W}$ ${\ displaystyle K}$${\ displaystyle \ lambda, \ mu \ in K}$

${\ displaystyle T \ left (\ lambda x + \ mu y \ right) = \ lambda T \ left (x \ right) + \ mu T \ left (y \ right)}$

gjelder.

eksempel

Er og er da en reell vektor og et reelt tall. Man velger nå for den lineære kartleggingen ${\ displaystyle V = \ mathbb {R} ^ {n}}$${\ displaystyle W = \ mathbb {R}}$${\ displaystyle x = (x_ {1}, \ dotsc, x_ {n}) \ i \ mathbb {R} ^ {n}}$${\ displaystyle b \ in \ mathbb {R}}$${\ displaystyle T}$

${\ displaystyle T (x) = a \ cdot x}$

med en konstant vektor , hvor er det skalære standardproduktet til de to vektorene, så oppnår man den lineære vektorligningen ${\ displaystyle a = (a_ {1}, \ dotsc, a_ {n}) \ in \ mathbb {R} ^ {n}}$${\ displaystyle (\ cdot)}$

${\ displaystyle a \ cdot x = b}$,

som tilsvarer den ovennevnte skalære lineære ligningen med ukjente. Den linearitet av følger direkte fra lineariteten til skalar multiplikasjon${\ displaystyle n}$${\ displaystyle T}$

${\ displaystyle T (\ lambda x + \ mu y) = a \ cdot (\ lambda x + \ mu y) = \ lambda (a \ cdot x) + \ mu (a \ cdot y) = \ lambda T (x ) + \ mu T (y)}$.

homogenitet

En homogen og en inhomogen skalar lineær ligning med to ukjente og${\ displaystyle x_ {1}}$${\ displaystyle x_ {2}}$

En lineær ligning kalles homogen hvis det er, det vil si hvis den har formen ${\ displaystyle b = 0}$

${\ displaystyle T (x) = 0}$

ellers kalles en lineær ligning inhomogen. Homogene lineære ligninger har minst nullvektoren

${\ displaystyle x = 0}$

som en løsning, der

${\ displaystyle T (0) = T (0 \ cdot 0) = 0 \ cdot T (0) = 0}$

gjelder. Omvendt blir inhomogene lineære ligninger ikke oppfylt av den trivielle løsningen.

eksempel

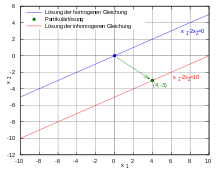
Løsningen av den homogene lineære ligningen med to ukjente og${\ displaystyle x_ {1}}$${\ displaystyle x_ {2}}$

${\ displaystyle 3x_ {1} + 4x_ {2} = 0}$

er en rett linje i todimensjonalt rom som går gjennom nullpunktet . Løsningen på den inhomogene ligningen

${\ displaystyle 3x_ {1} + 4x_ {2} = 12}$

er en rett linje parallell med den , men som ikke inneholder nullpunktet.

Superposisjon

Superposisjonsprinsipp i den lineære ligningen : løsning av den homogene ligningen (blå), partikkeloppløsningen (grønn) og løsningen av den inhomogene ligningen (rød)${\ displaystyle x_ {1} -2x_ {2} = 10}$

Homogene lineære ligninger har superposisjonsegenskapen : La og to løsninger av en homogen lineær ligning, så er det også en løsning av denne ligningen. Generelt er det til og med sant at alle lineære kombinasjoner av løsninger av en homogen lineær ligning med konstanter og løser denne ligningen, da ${\ displaystyle {\ hat {x}}}$${\ displaystyle {\ bar {x}}}$${\ displaystyle {\ hat {x}} + {\ bar {x}}}$${\ displaystyle c {\ hat {x}} + d {\ bar {x}}}$${\ displaystyle c}$${\ displaystyle d}$

${\ displaystyle T (c {\ hat {x}} + d {\ bar {x}}) = T (c {\ hat {x}}) + T (d {\ bar {x}}) = cT ( {\ hat {x}}) + dT ({\ bar {x}}) = 0 + 0 = 0}$

gjelder. Ved å inkludere og superposisjonsegenskapen danner løsningene til en homogen lineær ligning et underområde av . ${\ displaystyle x = 0}$${\ displaystyle V}$

Videre kan løsningen av en inhomogen ligning representeres som summen av løsningen av den tilknyttede homogene ligningen og en bestemt løsning: La en konkret løsning av en inhomogen lineær ligning være den generelle løsningen på det tilknyttede homogene problemet, så den generelle løsningen av den inhomogene ligningen er der ${\ displaystyle {\ bar {x}}}$${\ displaystyle y}$${\ displaystyle y + {\ bar {x}}}$

${\ displaystyle T (y + {\ bar {x}}) = T (y) + T ({\ bar {x}}) = 0 + b = b}$

gjelder. Løsningene til en inhomogen lineær ligning danner således et affint underrom over vektorområdet til den tilhørende homogene ligningen.

Motsatt gjelder følgende tilsvarende: Hvis og er to løsninger av en inhomogen lineær ligning, løser den tilhørende homogene ligningen, da ${\ displaystyle {\ hat {x}}}$${\ displaystyle {\ bar {x}}}$${\ displaystyle {\ hat {x}} - {\ bar {x}}}$

${\ displaystyle T ({\ hat {x}} - {\ bar {x}}) = T ({\ hat {x}}) - T ({\ bar {x}}) = bb = 0}$

gjelder.

eksempel

En konkret løsning på den inhomogene ligningen

${\ displaystyle x_ {1} -2x_ {2} = 10}$

er

${\ displaystyle {\ bar {x}} _ {1} = 4, {\ bar {x}} _ {2} = - 3}$.

Er nå løsningene til den tilsvarende homogene ligningen ${\ displaystyle y = (y_ {1}, y_ {2})}$

${\ displaystyle y_ {1} -2y_ {2} = 0}$,

så alt sammen , da blir den inhomogene ligningen vanligvis løst av ${\ displaystyle y}$${\ displaystyle y_ {1} = 2y_ {2}}$

${\ displaystyle x = y + {\ bar {x}} = (y_ {1} + {\ bar {x}} _ {1}, y_ {2} + {\ bar {x}} _ {2}) = (2y_ {2} + 4, y_ {2} -3) = (2t + 4, t-3)}$  med   .${\ displaystyle t \ in \ mathbb {R}}$

Dimensjon på løsningsområdet

Den løsning plass av en homogen lineær ligning kalles kjerne av den lineære kartlegging, dens dimensjon er også kalt en defekt . På grunn av rangsetningen gjelder en endelig dimensjonal homogen lineær ligning for dimensjonen til løsningsrommet ${\ displaystyle \ mathrm {ker} (T)}$

${\ displaystyle \ mathrm {dim} (\ mathrm {ker} (T)) = \ dim (V) - \ mathrm {rank} (T)}$.

Her er den rangeringen av bildet, dvs. dimensjonen av sitt image . Bildet av et bilde er settet med verdier som kan antas for . ${\ displaystyle \ mathrm {rank} (T)}$${\ displaystyle T (x)}$${\ displaystyle x \ i V}$

På grunn av superposisjonsegenskapen er dimensjonen til løsningsrommet til en inhomogen lineær ligning den samme som den tilhørende homogene ligningen, forutsatt at en bestemt løsning eksisterer. Dette er nøyaktig tilfelle når høyre side er i bildet av figuren, så følgende gjelder. Den koks Kjernen i den lineære kartlegging presist beskriver den plass av forhold som den høyre side av en lineær ligning, må oppfylle for at ligningen for å være løsbar. Dimensjonen er ${\ displaystyle b}$${\ displaystyle b \ i T (V)}$${\ displaystyle \ mathrm {coker} (T) = W / T (V)}$

${\ displaystyle \ mathrm {dim} (\ mathrm {coker} (T)) = \ mathrm {dim} (W) - \ mathrm {rank} (T)}$.

Eksempler

Man velger som vektorrom og så vel som lineær kartlegging ${\ displaystyle V = \ mathbb {R} ^ {3}}$${\ displaystyle W = \ mathbb {R}}$

${\ displaystyle T (x) = a_ {1} x_ {1} + a_ {2} x_ {2} + a_ {3} x_ {3}}$,

der minst en av koeffisientene ikke er lik null, så er bildet av hele rommet og dermed ${\ displaystyle a_ {1}, a_ {2}, a_ {3}}$${\ displaystyle T}$${\ displaystyle W}$

${\ displaystyle \ mathrm {dim} (\ mathrm {ker} (T)) = \ dim (\ mathbb {R} ^ {3}) - \ dim (\ mathbb {R}) = 3-1 = 2}$.

Løsningsrommet til den homogene lineære ligningen har dimensjon 2 og er et plan i tredimensjonalt rom. Løsningsrommet til den inhomogene ligningen er også et nivå her, siden ligningen, for eksempel , har partikkeloppløsningen . Kokskjernen her har dimensjon 0, slik at ligningen kan løses for hva som helst. ${\ displaystyle T (x) = 0}$${\ displaystyle T (x) = b}$${\ displaystyle a_ {1} \ neq 0}$${\ displaystyle (b / a_ {1}, 0,0)}$${\ displaystyle b}$

Hvis du velger i stedet

${\ displaystyle T (x) = 0x_ {1} + 0x_ {2} + 0x_ {3}}$,

så er alle vektorer fra kartlagt til null og det gjelder ${\ displaystyle V}$

${\ displaystyle \ mathrm {dim} (\ mathrm {ker} (T)) = \ dim (\ mathbb {R} ^ {3}) - \ dim (\ {0 \}) = 3-0 = 3}$.

Løsningsrommet til den tilsvarende homogene lineære ligningen er derfor hele det tredimensjonale rommet. Løsningsrommet til den inhomogene ligningen er tomt i dette tilfellet, siden ligningen bare har en løsning. Kokskjernen har dimensjon 1. ${\ displaystyle b = 0}$

Viktige typer lineære ligninger

Lineære diofantiske ligninger

Hvis man velger vektorrom og over hele tall og ${\ displaystyle V = \ mathbb {Z} ^ {n}}$${\ displaystyle W = \ mathbb {Z}}$

${\ displaystyle T (x) = a \ cdot x}$

med en konstant koeffisientvektor oppnår man de lineære diofantiske ligningene${\ displaystyle a \ in \ mathbb {Z} ^ {n}}$

${\ displaystyle a_ {1} x_ {1} + a_ {2} x_ {2} + \ dotsb + a_ {n} x_ {n} = b}$,

hvorav heltalsløsninger blir søkt. Lineære diofantiske ligninger har løsninger hvis den største felles divisoren til koeffisientene opp til er en divisor på høyre side , dvs. hvis ${\ displaystyle x = (x_ {1}, \ dotsc, x_ {n}) \ i \ mathbb {Z} ^ {n}}$${\ displaystyle a_ {1}}$${\ displaystyle a_ {n}}$${\ displaystyle b}$

${\ displaystyle \ operatorname {ggT} (a_ {1}, \ dotsc, a_ {n}) \; | \; b}$

gjelder. Løsningene kan deretter gis ved å kombinere løsningene i den homogene ligningen med en partikkelformet løsning som kan bli funnet ved hjelp av den utvidede euklidiske algoritmen .

Lineære vektorligninger

Hvis man velger vektorrom og også ${\ displaystyle V = \ mathbb {R} ^ {n}}$${\ displaystyle W = \ mathbb {R} ^ {m}}$

${\ displaystyle T (x) = A \; \ cdot \; x = {\ begin {pmatrix} a_ {11} & a_ {12} & \ cdots & a_ {1n} \\ a_ {21} & a_ {22 } & \ cdots & a_ {2n} \\\ vdots & \ vdots & \ ddots & \ vdots \\ a_ {m1} & a_ {m2} & \ cdots & a_ {mn} \\\ end {pmatrix}} \ cdot {\ begin {pmatrix} x_ {1} \\ x_ {2} \\\ vdots \\ x_ {n} \\\ end {pmatrix}} = {\ begin {pmatrix} a_ {11} x_ {1} + a_ {12} x_ {2} + \ cdots + a_ {1n} x_ {n} \\ a_ {21} x_ {1} + a_ {22} x_ {2} + \ cdots + a_ {2n} x_ { n} \\\ vdots \\ a_ {m1} x_ {1} + a_ {m2} x_ {2} + \ cdots + a_ {mn} x_ {n} \\\ end {pmatrix}},}$

karakterisert ved at en ekte - matrise oppnås den lineære vektor ligning ${\ displaystyle A \ in \ mathbb {R} ^ {m, n}}$${\ displaystyle m \ times n}$

${\ displaystyle A \ cdot x = b}$

med høyre side og ukjent vektor , som bare representerer et lineært ligningssystem . Et lineært ligningssystem opprettes således ved å kombinere flere skalære lineære ligninger med en eller flere ukjente i en enhet. Løsningssettet til et lineært ligningssystem er da skjæringspunktet mellom løsningene til de enkelte ligningene. Et lineært ligningssystem kan løses hvis og bare hvis rangen til koeffisientmatrisen er lik rangeringen til den utvidede koeffisientmatrisen . Lineære ligningssystemer kan for eksempel løses ved hjelp av den Gaussiske eliminasjonsmetoden . ${\ displaystyle b \ in \ mathbb {R} ^ {m}}$${\ displaystyle x \ in \ mathbb {R} ^ {n}}$${\ displaystyle A}$ ${\ displaystyle (A \; b)}$

Lineære forskjellsligninger

Hvis man velger vektorrom som sekvensrom, og ${\ displaystyle V = W = \ mathbb {R} ^ {\ mathbb {N}}}$

${\ displaystyle T ((x_ {n}) _ {n}) = \ sum _ {i = 0} ^ {k} a_ {i} (n) x_ {ni}}$

man oppnår den lineære forskjellsligningen - rekkefølge ${\ displaystyle k}$

${\ displaystyle a_ {0} (n) x_ {n} + a_ {1} (n) x_ {n-1} + \ dotsb + a_ {k} (n) x_ {nk} = b (n)}$  for   ,${\ displaystyle n \ in \ mathbb {N}, n \ geq k}$

der det ukjente er en sekvens og og er koeffisienter som kan avhenge av, men må være uavhengig av vilkårene for den sekvensen som søkes. Løsningen på en differensligning avhenger av startverdiene og er så klart definert. Lineære forskjellsligninger kan eksplisitt løses ved å kombinere løsningen av den homogene ligningen, som kan bli funnet ved hjelp av den karakteristiske ligningen , med en partikkeloppløsning. ${\ displaystyle (x_ {n}) _ {n} \ in \ mathbb {R} ^ {\ mathbb {N}}}$${\ displaystyle a_ {0} (n), \ dotsc, a_ {k} (n)}$${\ displaystyle b (n)}$${\ displaystyle n}$${\ displaystyle x_ {0}, \ dotsc, x_ {k-1}}$

Lineære vanlige differensialligninger

Hvis man velger vektorrom og som funksjonsrom med kontinuerlig differensierbare funksjoner, og man oppnår -th orden som lineær ordinær differensialoperatør ved å velge${\ displaystyle V}$${\ displaystyle W}$ ${\ displaystyle f \ i C ^ {n}}$${\ displaystyle g \ i C ^ {0}}$${\ displaystyle T}$ ${\ displaystyle n}$

${\ displaystyle T (f) = \ left (\ sum _ {i = 0} ^ {n} a_ {i} (x) {\ frac {d ^ {i}} {dx ^ {i}}} \ right ) f}$

den lineære ordinære differensiallikningen

${\ displaystyle a_ {n} (x) f ^ {(n)} (x) + \ dotsb + a_ {1} (x) f '(x) + a_ {0} (x) f (x) = g (x)}$,

der koeffisientfunksjonene og høyre side kan avhenge av , men ikke av, funksjonen som er søkt og dens derivater . Hvis en vektors funksjon brukes, snakker man om et lineært differensiallikningssystem . Picard-Lindelöfs teorem gir eksistensen og unikheten til løsningen av vanlige differensiallikninger av første orden . Den generelle løsningen av den homogene ligningen kan gis via det tilhørende grunnleggende systemet, en bestemt løsning kan for eksempel bli funnet ved å variere konstantene . ${\ displaystyle a_ {0}, \ dotsc, a_ {n}}$${\ displaystyle g}$${\ displaystyle x}$${\ displaystyle f}$${\ displaystyle f ', \ dotsc, f ^ {(n)}}$${\ displaystyle f}$

Lineære delvise differensialligninger

Hvis vektorrommene og også funksjonsrommene, hvor og er kontinuerlig differensierbare funksjoner av flere variabler , oppnår man -th orden som den lineære, delvise differensialoperatøren ved å velge${\ displaystyle V}$${\ displaystyle W}$${\ displaystyle f \ i C ^ {n}}$${\ displaystyle g \ i C ^ {0}}$${\ displaystyle T}$ ${\ displaystyle n}$

${\ displaystyle T (f) = \ left (\ sum _ {\ alpha _ {1} = 0} ^ {n} \ cdots \ sum _ {\ alpha _ {m} = 0} ^ {n} a _ { \ alpha} (x) {\ frac {\ partial ^ {| \ alpha |}} {\ partial x_ {1} ^ {\ alpha _ {1}} \ cdots \ partial x_ {m} ^ {\ alpha _ { m}}}} \ høyre) f}$

den lineære partielle differensiallikningen

${\ displaystyle \ sum _ {\ alpha _ {1} = 0} ^ {n} \ cdots \ sum _ {\ alpha _ {m} = 0} ^ {n} a _ {\ alpha} (x) {\ frac {\ partial ^ {| \ alpha |} f (x)} {\ partial x_ {1} ^ {\ alpha _ {1}} \ cdots \ partial x_ {m} ^ {\ alpha _ {m}}} } = g (x)}$,

hvor , og er. Igjen kan koeffisientfunksjonene og høyre side avhenge av koordinatene til , men ikke av funksjonen som er søkt og dens delvise derivater . For at løsningen av en delvis differensialligning skal være unikt bestemt, må innledende og / eller grensebetingelser spesifiseres. Det er forskjellige tilnærminger for å løse lineære partielle differensiallikninger, for eksempel grunnleggende løsninger , karakteristikkmetoden eller separasjonsmetoden . ${\ displaystyle x = (x_ {1}, \ dotsc, x_ {m})}$${\ displaystyle \ alpha = (\ alpha _ {1}, \ dotsc, \ alpha _ {m})}$${\ displaystyle | \ alpha | = \ alpha _ {1} + \ dotsb + \ alpha _ {m}}$${\ displaystyle a _ {\ alpha}}$${\ displaystyle g}$${\ displaystyle x_ {1}}$${\ displaystyle x_ {m}}$${\ displaystyle f}$

Lineære integrerte ligninger

Hvis vektorrom og funksjonsrom er tilstrekkelig integrerbare, oppnår man ved å velge som den lineære integraloperatøren${\ displaystyle V}$${\ displaystyle W}$${\ displaystyle T}$

${\ displaystyle T (f) = \ lambda f (x) + \ int _ {a} ^ {x} K (x, y) f (y) ~ dy}$

med integral kjerne og konstant prefaktor den lineære integrale ligningen${\ displaystyle K (x, y)}$${\ displaystyle \ lambda}$

${\ displaystyle \ lambda f (x) + \ int _ {a} ^ {x} K (x, y) f (y) ~ dy = g (x)}$,

som generelt sett representerer en Volterra integralligning av 2. type . Hvis begge integrasjonsgrensene er faste, er det en Fredholm integralligning. Hvis man snakker om en integrert ligning av den første typen . ${\ displaystyle \ lambda = 0}$

Flere lineære operatorligninger

Eksempler på ytterligere lineære operatørligninger med funksjoner som ukjente er:

• Lineære differensialgebraiske ligninger
• Lineære integrerte differensialligninger
• Lineære stokastiske differensialligninger

Se også

• Kvadratisk ligning
• Kubisk ligning
• Kvartisk ligning
• Linearisering

litteratur

• Hans Wilhelm Alt : Lineær funksjonsanalyse. En applikasjonsorientert introduksjon . 5. utgave. Springer-Verlag, 2008, ISBN 3-540-34186-2 . 
• Bernd Aulbach : Vanlige differensiallikninger . 2. utgave. Spectrum Academic Publishing House, 2004, ISBN 3-8274-1492-X . 
• Albrecht Beutelspacher : Lineær algebra. En introduksjon til vitenskapen om vektorer, kart og matriser . 7. utgave. Vieweg, 2009, ISBN 3-528-66508-4 . 
• Peter Bundschuh : Introduksjon til tallteori . 6. utgave. Springer-Verlag, 2010, ISBN 3-540-76490-9 . 
• Gerd Fischer : Lineær algebra. En introduksjon for førsteårsstudenter . 17. utgave. Vieweg Verlag, 2009, ISBN 3-8348-0996-9 . 
• Günter Gramlich: Lineær algebra . Fachbuchverlag Leipzig i Carl Hanser Verlag, 2003, ISBN 3-446-22122-0 . 
• Jürgen Jost : Partielle differensiallikninger. Elliptiske (og parabolske) ligninger . 1. utgave. Springer-Verlag, 2009, ISBN 3-540-64222-6 . 

weblenker

• MI Voitsekhovskii: Lineær ligning . I: Michiel Hazewinkel (red.): Encyclopedia of Mathematics . Springer-Verlag og EMS Press, Berlin 2002, ISBN 978-1-55608-010-4 (engelsk, online ). 
• Eric W. Weisstein : Lineær ligning . På: MathWorld (engelsk).
• Robert Milson: Lineær ligning . I: PlanetMath . (Engelsk)