Lineær illustrasjon

Akserefleksjon som et eksempel på en lineær kartlegging

En lineær kartlegging (også kalt lineær transformasjon eller vektorromhomomorfisme ) er en viktig type kartlegging mellom to vektorrom over samme felt i lineær algebra . Når det gjelder en lineær kartlegging, er det irrelevant om du først legger til to vektorer og deretter kartlegger summen, eller kartlegger vektorene først og deretter legger til summen av bildene. Det samme gjelder for multiplikasjon med en skalar fra grunnlegemet.

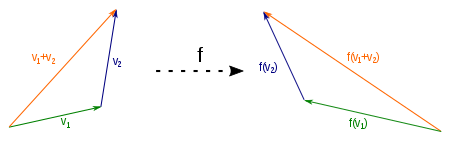
Eksemplet vist med en refleksjon på Y-aksen illustrerer dette. Vektoren er summen av vektorene , og dens bilde er vektoren . Men du får også hvis du legger til bildene og vektorene og . ${\ displaystyle c}$${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle {c '}}$${\ displaystyle {c '}}$${\ displaystyle {a '}}$${\ displaystyle {b '}}$${\ displaystyle a}$${\ displaystyle b}$

Man sier da at en lineær kartlegging er kompatibel med kombinasjonene av vektortilsetning og skalar multiplikasjon . Den lineære kartleggingen er altså en homomorfisme (strukturbevarende kartlegging) mellom vektorrom.

I funksjonell analyse , når man vurderer uendelig-dimensjonale vektorrom som har en topologi , snakker man vanligvis om lineære operatorer i stedet for lineære kartlegginger. Fra et formelt synspunkt er begrepene synonyme. Når det gjelder uendelige dimensjonale vektorrom, er imidlertid kontinuitetsspørsmålet viktig, mens kontinuitet alltid er til stede i lineære kartlegginger mellom endelige dimensjonale virkelige vektorrom (hver med den euklidiske normen ) eller, mer generelt, mellom endedimensjonale Hausdorff topologiske vektorrom .

definisjon

Vær og vektor mellomrom over en felles grunnleggende kropp . En kartlegging kalles en lineær kartlegging hvis alle og følgende betingelser gjelder: ${\ displaystyle V}$${\ displaystyle W}$ ${\ displaystyle K}$${\ displaystyle f \ colon V \ to W}$${\ displaystyle x, y \ i V}$${\ displaystyle a \ in K}$

• ${\ displaystyle f}$ er homogen:

  ${\ displaystyle f \ left (ax \ right) = af \ left (x \ right)}$

• ${\ displaystyle f}$ er tilsetningsstoff:

  ${\ displaystyle f \ left (x + y \ right) = f \ left (x \ right) + f \ left (y \ right)}$

De to forholdene ovenfor kan også oppsummeres:

${\ displaystyle f \ left (ax + y \ right) = af \ left (x \ right) + f \ left (y \ right)}$

For dette går inn i tilstanden for homogenitet og for additiviteten. En annen, likeverdig betingelse er kravet om at grafen til kartleggingen er et underområde av summen av vektorområdene og . ${\ displaystyle y = 0_ {V}}$${\ displaystyle a = 1_ {K}}$${\ displaystyle f}$${\ displaystyle V}$${\ displaystyle W}$

Forklaring

En kartlegging er lineær hvis den er kompatibel med vektorromsstrukturen. Med andre ord: lineære kartlegginger er kompatible med både den underliggende tillegg og skalar multiplikasjon av definisjons- og verdidomenet. Kompatibiliteten med tillegget betyr at den lineære kartleggingen mottar summer. Hvis vi har en sum med i definisjonsområdet , er denne summen gyldig og forblir dermed i verdiområdet i henhold til illustrasjonen: ${\ displaystyle f \ colon V \ to W}$${\ displaystyle v_ {3} = v_ {1} + v_ {2}}$${\ displaystyle v_ {1}, v_ {2}, v_ {3} \ in V}$${\ displaystyle f (v_ {3}) = f (v_ {1}) + f (v_ {2})}$

${\ displaystyle \ forall v_ {1}, v_ {2}, v_ {3} \ in V {\ Big (} v_ {3} = v_ {1} + v_ {2} \ impliserer f (v_ {3}) = f (v_ {1}) + f (v_ {2}) {\ Big)}}$

Denne implikasjonen kan forkortes ved å legge premissene inn . Slik får du etterspørselen . Kompatibiliteten med skalar multiplikasjon kan beskrives analogt. Dette oppfylles hvis det følger av forbindelsen med skalaren og i definisjonsområdet at følgende også gjelder i verdiområdet: ${\ displaystyle v_ {3} = v_ {1} + v_ {2}}$${\ displaystyle f (v_ {3}) = f (v_ {1}) + f (v_ {2})}$${\ displaystyle f (v_ {1} + v_ {2}) = f (v_ {1}) + f (v_ {2})}$${\ displaystyle {\ tilde {v}} = \ lambda v}$${\ displaystyle \ lambda \ i K}$${\ displaystyle v \ in V}$${\ displaystyle f ({\ tilde {v}}) = \ lambda f (v)}$

${\ displaystyle \ forall {\ tilde {v}}, v \ i V \, \ forall \ lambda \ i K {\ Big (} {\ tilde {v}} = \ lambda v \ innebærer f ({\ tilde { v}}) = \ lambda f (v) {\ Big)}}$

Etter å ha lagt premissene inn i konklusjonen , mottar man kravet . ${\ displaystyle {\ tilde {v}} = \ lambda v}$${\ displaystyle f ({\ tilde {v}}) = \ lambda f (v)}$${\ displaystyle f (\ lambda v) = \ lambda f (v)}$

• 

  Visualisering av kompatibiliteten med vektortilsetning: Hver tilleggstrekant gitt av , og beholdes av den lineære kartleggingen . Også , og danner en tilleggstrekant, og den gjelder . ${\ displaystyle v_ {1}}$${\ displaystyle v_ {2}}$${\ displaystyle v_ {3} = v_ {1} + v_ {2}}$${\ displaystyle f}$${\ displaystyle f (v_ {1})}$${\ displaystyle f (v_ {2})}$${\ displaystyle f (v_ {1} + v_ {2})}$${\ displaystyle f (v_ {1} + v_ {2}) = f (v_ {1}) + f (v_ {2})}$

• 

  For kartlegginger som ikke er kompatible med tillegg, er det vektorer , og slik at , og ikke danner en tilleggstrekant fordi det er. En slik kartlegging er ikke lineær. ${\ displaystyle v_ {1}}$${\ displaystyle v_ {2}}$${\ displaystyle v_ {3} = v_ {1} + v_ {2}}$${\ displaystyle f (v_ {1})}$${\ displaystyle f (v_ {2})}$${\ displaystyle f (v_ {1} + v_ {2})}$${\ displaystyle f (v_ {1} + v_ {2}) \ neq f (v_ {1}) + f (v_ {2})}$

• 

  Visualisering av kompatibiliteten med skalar multiplikasjon: Hver skalering beholdes ved en lineær kartlegging og den gjelder . ${\ displaystyle \ lambda v}$${\ displaystyle f (\ lambda v) = \ lambda f (v)}$

• 

  Hvis en kartlegging ikke er kompatibel med skalarmultiplikasjonen, er det en skalar og en vektor slik at skaleringen ikke blir kartlagt på skaleringen . En slik kartlegging er ikke lineær. ${\ displaystyle \ lambda}$${\ displaystyle v}$${\ displaystyle \ lambda v}$${\ displaystyle \ lambda f (v)}$

Eksempler

• For hver lineær kartlegging har formen med .${\ displaystyle V = W = \ mathbb {R}}$${\ displaystyle f (x) = mx}$${\ displaystyle m \ in \ mathbb {R}}$
• Det være og . Da en lineær kartlegging blir definert for hver matrise ved hjelp av matrise multiplikasjon . Enhver lineær kartlegging fra til kan representeres på denne måten.${\ displaystyle V = \ mathbb {R} ^ {n}}$${\ displaystyle W = \ mathbb {R} ^ {m}}$${\ displaystyle m \ times n}$${\ displaystyle A}$
  ${\ displaystyle f \ colon \ mathbb {R} ^ {n} \ to \ mathbb {R} ^ {m}}$
  
  ${\ displaystyle f (x) = A \, x = {\ begin {pmatrix} a_ {11} & \ dots & a_ {1n} \\\ vdots && \ vdots \\ a_ {m1} & \ dots & a_ {mn} \ end {pmatrix}} {\ begin {pmatrix} x_ {1} \\\ vdots \\ x_ {n} \ end {pmatrix}}}$
  ${\ displaystyle \ mathbb {R} ^ {n}}$${\ displaystyle \ mathbb {R} ^ {m}}$
• Er et åpent intervall av vektorrommet av de stadig deriverbare funksjoner og den vektorrommet av de kontinuerlige funksjoner på , slik at bildet er , , at hver funksjon tildeler dens deriverte, lineær. Det samme gjelder andre lineære differensialoperatører .${\ displaystyle I \ subset \ mathbb {R}}$${\ displaystyle V = C ^ {1} (I, \ mathbb {R})}$${\ displaystyle \ mathbb {R}}$${\ displaystyle I}$${\ displaystyle W = C ^ {0} (I, \ mathbb {R})}$${\ displaystyle \ mathbb {R}}$${\ displaystyle I}$
  ${\ displaystyle D \ kolon C ^ {1} (I, \ mathbb {R}) \ til C ^ {0} (I, \ mathbb {R})}$${\ displaystyle f \ mapsto f '}$
  ${\ displaystyle f \ i C ^ {1} (I, \ mathbb {R})}$

• 

  Tøyningen er et lineært kart. I denne illustrasjonen strekkes komponenten av faktoren . ${\ displaystyle f (x, y) = (2x, y)}$${\ displaystyle x}$${\ displaystyle 2}$

• 

  Dette tallet er tilsetning: Det spiller ingen rolle om bare å legge vektorer og kartlegging eller om bare kartlegger vektorer og deretter la til: . ${\ displaystyle f (a + b) = f (a) + f (b)}$

• 

  Dette tallet er homogen: det spiller ingen rolle om du bare skalert en vektor og deretter kartlegging eller om bare over og deretter skalerer vektoren: . ${\ displaystyle f (\ lambda a) = \ lambda f (a)}$

Bilde og kjerne

To sett med betydning når man ser på lineære kart er bildet og kjernen til et lineært kart . ${\ displaystyle f \ colon V \ to W}$

• Bildet av illustrasjonen er det sett med bilde vektorer under , dvs. settet av alle med ut . Mengden bilder noteres derfor også av. Bildet er et underrom av .${\ displaystyle \ mathrm {im} (f)}$${\ displaystyle f}$${\ displaystyle f (v)}$${\ displaystyle v}$${\ displaystyle V}$${\ displaystyle f (V)}$${\ displaystyle W}$

• Kjernen i kartleggingen er settet med vektorer som blir kartlagt på nullvektoren av by. Det er et underrom av . Kartleggingen er injeksjonsdyktig hvis og bare hvis kjernen bare inneholder nullvektoren.${\ displaystyle \ mathrm {ker} (f)}$${\ displaystyle V}$${\ displaystyle f}$${\ displaystyle W}$${\ displaystyle V}$${\ displaystyle f}$

kjennetegn

• Et lineært kart mellom vektorrom og danner nullvektoren til nullvektoren fra fra: fordi${\ displaystyle V}$${\ displaystyle W}$${\ displaystyle V}$${\ displaystyle W}$
  ${\ displaystyle f (0_ {V}) = 0_ {W}}$${\ displaystyle f \ left (0_ {V} \ right) = f \ left (0 \ cdot 0_ {V} \ right) = 0 \ cdot f \ left (0_ {V} \ right) = 0_ {W}. }$
• The homomorphism theorem beskriver en sammenheng mellom kjernen og bildet av en lineær kartlegging : Faktorrommet er isomorf til bildet .${\ displaystyle f \ colon V \ to W}$ ${\ displaystyle V / \ mathrm {ker} (f)}$${\ displaystyle \ mathrm {im} (f)}$

Lineære kartlegginger mellom endedimensjonale vektorrom

Utgangspunkt

Oppsummering av egenskapene til injiserende og surjektiv lineære kartlegginger

En lineær kartlegging mellom endelige dimensjonale vektorrom bestemmes unikt av bildene av vektorene på en basis . Hvis vektorene danner et grunnlag for vektorrommet og er vektorer i , er det nøyaktig en lineær kartlegging som kartlegges på , på , ..., på . Hvis en hvilken som helst vektor er av , kan den vises tydelig som en lineær kombinasjon av basisvektorene: ${\ displaystyle b_ {1}, \ dotsc, b_ {n}}$${\ displaystyle V}$${\ displaystyle w_ {1}, \ dotsc, w_ {n}}$${\ displaystyle W}$${\ displaystyle f \ colon V \ to W}$${\ displaystyle b_ {1}}$${\ displaystyle w_ {1}}$${\ displaystyle b_ {2}}$${\ displaystyle w_ {2}}$${\ displaystyle b_ {n}}$${\ displaystyle w_ {n}}$${\ displaystyle v}$${\ displaystyle V}$

${\ displaystyle v = \ textstyle \ sum \ limits _ {j = 1} ^ {n} v_ {j} b_ {j}}$

Her er de koordinater til vektoren med hensyn til basen . Hans bilde er gitt av ${\ displaystyle v_ {1}, \ ldots, v_ {n}}$${\ displaystyle v}$${\ displaystyle \ {b_ {1}, \ dotsc, b_ {n} \}}$${\ displaystyle f (v)}$

${\ displaystyle f (v) = \ textstyle \ sum \ limits _ {j = 1} ^ {n} v_ {j} f (b_ {j}) = \ sum \ limits _ {j = 1} ^ {n} v_ {j} w_ {j}.}$

Kartleggingen er injeksjonsdyktig hvis og bare hvis bildvektorene til basen er lineært uavhengige . Det er antagelig hvis og bare hvis det spenner over målområdet . ${\ displaystyle f}$${\ displaystyle w_ {1}, \ dotsc, w_ {n}}$${\ displaystyle w_ {1}, \ dotsc, w_ {n}}$${\ displaystyle W}$

Hvis man tilordner hvert element av en base av en vektor fra vilkårlig, så er det mulig med den ovenfor angitte formel til en lineær kartlegging, denne oppgaven klart fortsette. ${\ displaystyle b_ {1}, \ dotsc, b_ {n}}$${\ displaystyle V}$${\ displaystyle w_ {1}, \ dotsc, w_ {n}}$${\ displaystyle W}$${\ displaystyle f \ colon V \ to W}$

Hvis bildvektorene er representert med hensyn til en base av , fører dette til matrisepresentasjonen av den lineære kartleggingen. ${\ displaystyle w_ {j}}$${\ displaystyle W}$

Kartleggingsmatrise

Er og endelig, , , og er baser på og fra der, kan hver lineær kartlegging ved en - matrise presenteres. Dette oppnås som følger: For hver basisvektor fra kan bildvektoren representeres som en lineær kombinasjon av basisvektorene : ${\ displaystyle V}$${\ displaystyle W}$${\ displaystyle \ dim V = n}$${\ displaystyle \ dim W = m}$${\ displaystyle B = \ {b_ {1}, \ dotsc, b_ {n} \}}$${\ displaystyle V}$${\ displaystyle B '= \ {b_ {1}', \ dotsc, b_ {m} '\}}$${\ displaystyle W}$${\ displaystyle f \ colon V \ to W}$${\ displaystyle m \ times n}$ ${\ displaystyle M_ {B '} ^ {B} (f)}$${\ displaystyle b_ {j}}$${\ displaystyle B}$${\ displaystyle f (b_ {j})}$${\ displaystyle b_ {1} ', \ dotsc, b_ {m}'}$

${\ displaystyle f (b_ {j}) = \ sum _ {i = 1} ^ {m} a_ {ij} b_ {i} '}$

Den , , er innleggene i matrisen : ${\ displaystyle a_ {ij}}$${\ displaystyle i = 1, \ dotsc, m}$${\ displaystyle j = 1, \ dotsc, n}$${\ displaystyle M_ {B '} ^ {B} (f)}$

${\ displaystyle M_ {B '} ^ {B} (f) = {\ begin {pmatrix} a_ {11} & \ dots & a_ {1j} & \ dots & a_ {1n} \\\ vdots && \ vdots && \ vdots \\ a_ {m1} & \ dots & a_ {mj} & \ dots & a_ {mn} \ end {pmatrix}}}$

Den -te kolonne inneholder koordinatene i forhold til basisen . ${\ displaystyle j}$${\ displaystyle f (b_ {j})}$${\ displaystyle B '}$

Ved hjelp av denne matrisen kan man beregne bildvektoren til hver vektor : ${\ displaystyle f (v)}$${\ displaystyle v = v_ {1} b_ {1} + \ dotsb + v_ {n} b_ {n} \ in V}$

${\ displaystyle f (v) = \ sum _ {j = 1} ^ {n} v_ {j} f (b_ {j}) = \ sum _ {j = 1} ^ {n} v_ {j} \ left (\ sum _ {i = 1} ^ {m} a_ {ij} b_ {i} '\ right) = \ sum _ {i = 1} ^ {m} \ left (\ sum _ {j = 1} ^ {n} a_ {ij} v_ {j} \ right) b_ {i} '}$

For koordinatene av respekt så sant ${\ displaystyle w_ {1}, \ dotsc, w_ {m}}$${\ displaystyle f (v)}$${\ displaystyle B '}$

${\ displaystyle w_ {i} = \ sum _ {j = 1} ^ {n} a_ {ij} v_ {j}}$.

Dette kan uttrykkes ved hjelp av matriksmultiplikasjon:

${\ displaystyle {\ begin {pmatrix} w_ {1} \\\ vdots \\ w_ {m} \ end {pmatrix}} = {\ begin {pmatrix} a_ {11} & \ dots & a_ {1n} \\\ vdots && \ vdots \\ a_ {m1} & \ dots & a_ {mn} \ end {pmatrix}} \, {\ begin {pmatrix} v_ {1} \\\ vdots \\ v_ {n} \ end {pmatrix} }}$

Matrisen kalles kartleggingsmatrisen eller representasjonsmatrisen til . Andre skrivemåter for er og . ${\ displaystyle M_ {B '} ^ {B} (f)}$${\ displaystyle f}$${\ displaystyle M_ {B '} ^ {B} (f)}$${\ displaystyle _ {B '} f_ {B}}$${\ displaystyle _ {B '} [f] _ {B}}$

Dimensjonsformel

Bilde og kjerne er relatert via settet med dimensjoner. Dette sier at dimensjonen er lik summen av dimensjonene til bildet og kjernen: ${\ displaystyle V}$

${\ displaystyle \ dim V = \ dim \ mathrm {ker} (f) + \ dim \ mathrm {im} (f)}$

Lineære kartlegginger mellom uendelig-dimensjonale vektorrom

Spesielt i funksjonell analyse vurderer man lineære kartlegginger mellom uendelig-dimensjonale vektorrom. I denne sammenheng kalles lineære kartlegginger vanligvis lineære operatorer. Vektorrommene som betraktes har vanligvis også tilleggsstrukturen til et normalisert komplett vektorrom. Slike vektorrom kalles Banach-mellomrom . I motsetning til det endelige dimensjonale tilfellet er det ikke tilstrekkelig å undersøke lineære operatører bare på et grunnlag. I følge Baiers kategorisetning har et grunnlag for et uendelig dimensjonalt Banach-rom et utallig antall elementer, og eksistensen av et slikt grunnlag kan ikke rettferdiggjøres konstruktivt, dvs. bare ved bruk av det valgte aksiomet . Et annet grunnleggende begrep blir derfor brukt, for eksempel ortonormale baser eller, mer generelt, rystebaser . Dette betyr at visse operatører som Hilbert-Schmidt-operatører kan bli representert ved hjelp av "uendelig store matriser", hvor uendelige lineære kombinasjoner da også må tillates.

Spesielle lineære kart

Monomorfisme

En monomorfisme mellom vektorrom er en lineær kartlegging som er injiserende . Dette gjelder nøyaktig når kolonnevektorene til representasjonsmatrisen er lineært uavhengige.${\ displaystyle f \ colon V \ to W}$

Epimorfisme

En epimorfisme mellom vektorrom er en lineær kartlegging som er antatt . Dette er tilfelle hvis og bare hvis rangeringen av representasjonsmatrisen er lik dimensjonen av .${\ displaystyle f \ colon V \ to W}$${\ displaystyle W}$

Isomorfisme

En isomorfisme mellom vektorrom er en lineær kartlegging som er bijektiv . Dette er nøyaktig tilfelle når skjermmatrisen er vanlig . De to mellomrommene og kalles da isomorfe.${\ displaystyle f \ colon V \ to W}$${\ displaystyle V}$${\ displaystyle W}$

Endomorfisme

En endomorphism mellom vektorrom er et lineært kart, hvor mellomrommene og er lik: . Representasjonsmatrisen til denne figuren er en kvadratmatrise.${\ displaystyle V}$${\ displaystyle W}$${\ displaystyle f \ kolon V \ til V}$

Automorfisme

En automorfisme mellom vektorrom er en bijektiv lineær kartlegging der mellomrommene og er like. Så det er både en isomorfisme og en endomorfisme. Skjermmatrisen i denne figuren er en vanlig matrise.${\ displaystyle V}$${\ displaystyle W}$

Lineære figurer vektor plass

Dannelse av vektorområdet L (V, W)

Settet med lineære kartlegginger fra et -vektorrom til et -vektorrom er et vektorrom over , mer presist: et underområde av -vektorområdet til alle kartlegginger fra til . Dette betyr at summen av to lineære kartlegginger og , komponentmessig definert av ${\ displaystyle L (V, W)}$${\ displaystyle K}$${\ displaystyle V}$${\ displaystyle K}$${\ displaystyle W}$${\ displaystyle K}$${\ displaystyle K}$${\ displaystyle V}$${\ displaystyle W}$${\ displaystyle f}$${\ displaystyle g}$

${\ displaystyle (f + g) \ colon x \ mapsto f (x) + g (x),}$

igjen er en lineær kartlegging og at produktet

${\ displaystyle (\ lambda f) \ colon x \ mapsto \ lambda f (x)}$

en lineær kartlegging med en skalar er også en lineær kartlegging igjen. ${\ displaystyle \ lambda \ i K}$

Hvis dimensjonen og dimensjonen , og er gitt i en base og en base , er kartleggingen ${\ displaystyle V}$${\ displaystyle n}$${\ displaystyle W}$${\ displaystyle m}$${\ displaystyle V}$${\ displaystyle B}$${\ displaystyle W}$${\ displaystyle C}$

${\ displaystyle L (V, W) \ til K ^ {m \ times n}, \ f \ mapsto M_ {C} ^ {B} (f)}$

en isomorfisme i matriksrommet . Vektorrommet har altså dimensjonen . ${\ displaystyle K ^ {m \ times n}}$${\ displaystyle L (V, W)}$${\ displaystyle m \ cdot n}$

Hvis du vurderer settet med lineære selvkartlegginger av et vektorrom, dvs. det spesielle tilfellet , så danner disse ikke bare et vektorrom, men også en assosiativ algebra med sammenkoblingen av kartlegginger som multiplikasjon , som kort omtales som ${\ displaystyle V = W}$${\ displaystyle L (V)}$

generalisering

En lineær kartlegging er et spesielt tilfelle av en affinekartlegging .

Hvis kroppen erstattes av en ring i definisjonen av den lineære kartleggingen mellom vektorrom , oppnås en modulhomomorfisme .

Notater og individuelle referanser

1. ↑ Dette settet med lineære kart er noen ganger også skrevet som.${\ displaystyle {\ text {Hom}} _ {K} (V, W)}$

litteratur

• Albrecht Beutelspacher : Lineær algebra. En introduksjon til vitenskapen om vektorer, kart og matriser. 6., reviderte og supplerte utgave. Vieweg Braunschweig et al. 2003, ISBN 3-528-56508-X , s. 124-143.
• Günter Gramlich: Lineær algebra. En introduksjon for ingeniører. Fachbuchverlag Leipzig i Carl-Hanser-Verlag, München 2003, ISBN 3-446-22122-0 .
• Detlef Wille: Gjentakelse av lineær algebra. Volum 1. 4. utgave, opptrykk. Binomi, Springe 2003, ISBN 3-923923-40-6 .

weblenker