Lineær kombinasjon

Vektoren er den lineære kombinasjonen${\ displaystyle {\ vec {v}}}$${\ displaystyle 2 {\ vec {u}} _ {1} +1,5 {\ vec {u}} _ {2}}$

${\ displaystyle v}$er en lineær kombinasjon av de to vektorene og . Det grønne planet representerer den lineære konvolutten til de to vektorene.${\ displaystyle v_ {1}}$${\ displaystyle v_ {2}}$

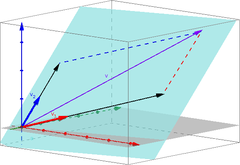
I lineær algebra forstås en lineær kombinasjon som en vektor som kan uttrykkes av gitte vektorer ved bruk av vektortilsetning og skalar multiplikasjon .

definisjon

Lineære kombinasjoner av endelig mange vektorer

La være et vektorrom over kroppen . I tillegg er et endelig antall vektorer fra gitt. Så kaller vi hver vektor som er i formen ${\ displaystyle V}$ ${\ displaystyle K}$ ${\ displaystyle v_ {1}, \ ldots, v_ {n}}$${\ displaystyle V}$${\ displaystyle v \ in V}$

${\ displaystyle v = a_ {1} v_ {1} + a_ {2} v_ {2} + \ dotsb + a_ {n} v_ {n} = \ sum _ {i = 1} ^ {n} a_ {i } v_ {i}}$

kan skrives med skalarer , en lineær kombinasjon av . Faktorene i illustrasjonen ovenfor kalles koeffisientene til den lineære kombinasjonen. Representasjonen i seg selv blir også referert til som en lineær kombinasjon. ${\ displaystyle a_ {1}, \ dotsc, a_ {n} \ in K}$${\ displaystyle v_ {1}, \ dotsc, v_ {n}}$${\ displaystyle a_ {1}, \ dotsc, a_ {n} \ in K}$

Eksempel: I det tredimensjonale ( reelle ) vektorrommet er vektoren en lineær kombinasjon av vektorene og , fordi ${\ displaystyle \ mathbb {R} ^ {3}}$${\ displaystyle v = \ left (\! {\ begin {smallmatrix} 16 \\ - 4 \\ 3 \ end {smallmatrix}} \! \ right)}$${\ displaystyle v_ {1} = \ left (\! {\ begin {smallmatrix} 3 \\ - 2 \\ 4 \ end {smallmatrix}} \! \ right)}$${\ displaystyle v_ {2} = \ left (\! {\ begin {smallmatrix} 2 \\ 0 \\ - 1 \ end {smallmatrix}} \! \ right)}$

${\ displaystyle {\ begin {pmatrix} 16 \\ - 4 \\ 3 \ end {pmatrix}} = 2 {\ begin {pmatrix} 3 \\ - 2 \\ 4 \ end {pmatrix}} + 5 {\ begin {pmatrix} 2 \\ 0 \\ - 1 \ end {pmatrix}}.}$

Koeffisientene og i dette eksemplet er reelle tall, fordi det er et reelt vektorrom. ${\ displaystyle a_ {1} = 2}$${\ displaystyle a_ {2} = 5}$${\ displaystyle \ mathbb {R} ^ {3}}$

Lineære kombinasjoner av et hvilket som helst antall vektorer

Lineære kombinasjoner av et uendelig antall elementer blir bare vurdert under forutsetningen om at i virkeligheten bare et endelig antall av dem blir brukt i summen.

La være en kropp og et vektorrom. La en familie av vektorer indekseres av indeks settet . Hvis man da har en koeffisient for hver slik at nesten alle koeffisientene er null, så er det ${\ displaystyle K}$${\ displaystyle V}$${\ displaystyle K}$${\ displaystyle (v_ {i}) _ {i \ i I}}$${\ displaystyle I}$${\ displaystyle v_ {i} \ in V}$${\ displaystyle i \ i I}$${\ displaystyle a_ {i} \ in K}$

${\ displaystyle v = \ sum _ {i \ i I} a_ {i} v_ {i}}$

den tilhørende lineære kombinasjonen. Det er nødvendig at bare endelig mange koeffisienter (og dermed summander) er forskjellige fra 0 slik at summen i det hele tatt kan defineres. En konvergent serie er derfor generelt ikke en lineær kombinasjon av summandene.

Lineære kombinasjoner i venstre moduler

I en videre generalisering er begrepet lineær kombinasjon allerede fornuftig hvis man vurderer ringer i stedet for kropper og venstre moduler i stedet for vektorrom. Mange av de enkle operasjonene som er kjent fra lineær algebra kan også utføres i denne allmenheten, bare å løse en vektor fra en lineær kombinasjon kan mislykkes, fordi du må multiplisere med det inverse av koeffisienten foran denne vektoren, og ringen inneholder dette inverse i vanligvis ikke.

Generell

I et vektorrom er hver lineær kombinasjon av vektorer igjen et element i vektorområdet. Settet med alle lineære kombinasjoner av et sett med vektorer kalles dets lineære konvolutt ; det er alltid et underområde for . Hvis alle vektorer i kan representeres som en lineær kombinasjon av et sett , er det et genererende system av . ${\ displaystyle V}$${\ displaystyle V}$${\ displaystyle V}$${\ displaystyle M}$${\ displaystyle M}$${\ displaystyle V}$

Den nullvektoren av et vektorrom alltid kan uttrykkes som en lineær kombinasjon av et gitt sett av vektorer. Hvis alle koeffisientene til en slik lineær kombinasjon er lik 0 (null element i den underliggende kroppen), snakker man om en triviell lineær kombinasjon. Hvis de gitte vektorene er lineært avhengige , kan nullvektoren også skrives som en ikke-triviell lineær kombinasjon. Generelt bestemmes koeffisientene til en lineær kombinasjon av vektorer nøyaktig når vektorene er lineært uavhengige.

Lineære kombinasjoner, hvis koeffisienter ikke er vilkårlige reelle eller komplekse tall, men hele tall (man snakker også om en integrert lineær kombinasjon ), spiller en sentral rolle i den utvidede euklidiske algoritmen ; det gir en fremstilling av den største fellesdeleren av to hele tall som en lineær kombinasjon av og : ${\ displaystyle a, b}$${\ displaystyle a}$${\ displaystyle b}$

${\ displaystyle \ operatorname {ggT} (a, b) = s \ cdot a + t \ cdot b}$.

Spesielle tilfeller

De spesielle lineære kombinasjonene som er vurdert her, bruker en ordre på koeffisientfeltet, de er derfor begrenset til - eller - vektorrom. ${\ displaystyle \ mathbb {R}}$${\ displaystyle \ mathbb {Q}}$

Positive koeffisienter

• Hvis koeffisientene til den lineære kombinasjonen er større enn eller lik null, snakker man om en konisk lineær kombinasjon . Hvis koeffisientene til den lineære kombinasjonen virkelig er større enn null, snakker man om en positiv kombinasjon .${\ displaystyle a_ {i}}$

Affine kombinasjon

• Hvis summen av koeffisientene er 1, er det en affin kombinasjon . Denne definisjonen er mulig for alle koblingsmoduler.

Konveks kombinasjon

I virkelige rom kalles en lineær kombinasjon for en konveks kombinasjon hvis alle koeffisienter kommer fra enhetsintervallet [0,1] og summen er 1:

${\ displaystyle v = a_ {1} v_ {1} + a_ {2} v_ {2} + \ dotsb + a_ {n} v_ {n} = \ sum _ {i = 1} ^ {n} a_ {i } v_ {i}, \ quad 0 \ leq a_ {i} \ leq 1, \ quad \ sum _ {i = 1} ^ {n} a_ {i} = 1}$.

Tilstanden kan utelates, fordi den skyldes automatisk den kumulative tilstanden og koeffisientenes ikke-negativitet. Med ovennevnte notasjon gjelder følgende i virkelige rom: En lineær kombinasjon er en konveks kombinasjon hvis og bare hvis den er konisk og affin. ${\ displaystyle a_ {i} \ leq 1}$

Konvekse kombinasjoner av konvekse kombinasjoner er igjen konvekse kombinasjoner. Settet med alle konvekse kombinasjoner av et gitt sett med vektorer kalles deres konvekse skrog .

litteratur

• Gerd Fischer : Lineær algebra. 14. reviderte utgave. Vieweg, Wiesbaden 2003, ISBN 3-528-03217-0 .