Firefargesett

Eksempel på firefarging

Kart over de amerikanske statene med fire farger

Den fire-farge teorem (også fire farger teoremet , tidligere også kjent som firefargers formodning eller firefargers problem ) er et matematisk teorem og sier at fire farger er alltid tilstrekkelig for enhver kartet i euklidske planet å være farget i på en slik måte at ikke to naboland får samme farge. Teoremet brukes i grafteori , topologi og kartografi .

Dette gjelder under begrensningene at isolerte fellespunkter ikke teller som "grenser", og at hvert land består av et sammenhengende område, så det er ingen eksklaver .

Formalisering

Representasjon av formuleringen i grafteori

Formelt er den enkleste måten å beskrive problemet på ved hjelp av grafteori . Man spør om nodene i hver plan graf kan farges med maksimalt fire farger på en slik måte at ingen noder til naboene har samme farge. Eller kort sagt: "Kan hver plangraf være firfarget ?" Hvert land på kartet er tildelt nøyaktig en node, og nodene i nabolandene er koblet til hverandre.

historie

Dette kortet krever fire forskjellige farger

Setningen ble først satt opp som en gjetning av Francis Guthrie i 1852 da han ønsket å farge fylkene i England på et kart. Det var åpenbart at tre farger ikke var nok, og fem ikke ville være nødvendig i noe konstruert eksempel. Antagelsen ble først diskutert og publisert i et brev fra London matteprofessor Augustus De Morgan datert 23. oktober 1852 til sin irske kollega William Rowan Hamilton : “Er fire eller færre farger nok til å farge landene på et kart slik at nabolandene har forskjellige farger slitasje? "

Den engelske matematikeren Arthur Cayley introduserte problemet for Mathematical Society of London i 1878. I løpet av bare ett år fant Alfred Kempe tilsynelatende bevis for setningen. Elleve år senere, i 1890, viste Percy Heawood at Kempes forsøk på å bevise at det var feil. Et andre feilaktig bevisforsøk, publisert av Peter Guthrie Tait i 1880 , kunne heller ikke tilbakevises på elleve år. Først i 1891 viste Julius Petersen at Taits tilnærming også var feil. Med imøtegåelse av Kempe “firefargeprøvetrykk” i 1890, Heawood ga også et bevis for de fem farger teorem , som en øvre grense for maling av plane kurver ble påvist feilfritt for første gang. Kempes defekte eksperiment inneholdt allerede grunnleggende ideer som førte til senere bevis av Appel og Haken.

Heinrich Heesch utviklet et første utkast til en datamaskin bevis i 1960 og 1970, men dette ble ikke realisert på grunn av mangel på regnetid. Dette ble forbedret av Kenneth Appel og Wolfgang Haken ved University of Illinois i 1976. Bevisene reduserte antall problematiske tilfeller fra uendelig til 1936 (en senere versjon til og med 1476), som ble kontrollert individuelt av en datamaskin. Etter kritikk av dette beviset publiserte Appel og Haken en detaljert beskrivelse i 1989 med et 400-siders vedlegg om mikrofilm.

I 1996 klarte Neil Robertson , Daniel Sanders , Paul Seymour og Robin Thomas å finne modifiserte databevis som reduserte tilfellene til 633. Disse måtte også kontrolleres av datamaskiner.

I 2005 konstruerte Georges Gonthier og Benjamin Werner et formelt bevis på teoremet i bevisassistenten Coq .

kritikk

Fire-fargesetningen var det første store matteproblemet som ble løst ved hjelp av datamaskiner . Derfor ble beviset ikke anerkjent av noen matematikere fordi det ikke kan forstås direkte av et menneske, og fordi man må stole på korrektheten til kompilatoren og maskinvaren . Mangelen på matematisk eleganse i beviset har også blitt kritisert. Allerede i 1989 uttrykte grafteoretikeren Horst Sachs eksplisitt den oppfatning at den endelige løsningen på firefargeproblemet fortsatt er ventet . Kritikken har vedvaret i nyere tid og er forsterket av den britiske matematikeren Ian Stewart .

Frimerket med tilleggsinnskrift Fire farger er tilstrekkelig , av matematikkavdelingen i UIUC , som Appel og Haken arbeidet med, brukt etter dataregistrering i 1976

Forsøk på å bevise

Noen kjente matematikere prøvde seg på beviset. Max Born rapporterer at Hermann Minkowski (1864–1909) forsøkte å bevise det over flere uker i et innledende foredrag om topologi (med innledningsordene at dette ville være en god introduksjon til topologi, og at bare tredjeklasses matematikere har prøvd det så langt ) til han til slutt ga opp. Born husker at det var tordenvær den gangen og Minkowski sa spøkende halvt at himmelen ville være sint på hans overmot.

Selv Ernst Witt prøvde på 1930-tallet som student på bevisene og presenterte det for Richard Courant ; hans venn Heinrich Heesch fant en feil, som var begynnelsen på hans egen opptatthet med problemet.

Andre matematikere som taklet problemet og oppnådde betydelige delresultater var Øystein Ore (som økte minimum antall områder som kan farges med fire farger til 40) og Hassler Whitney (i sin avhandling fra 1932).

Det er også algebraisk ekvivalente formuleringer ( Howard Levi , Juri Wladimirowitsch Matijassewitsch , M. Mnuk, Noga Alon ).

Kempes falske bevis

"Bevis"

Sak 2 - v med 4 naboer i 4 farger
Sak 3 - v med 5 naboer i 4 farger

I 1879 var Alfred Kempe en av de første matematikerne som prøvde å finne et bevis på firefargesetningen. Hans idé om å bruke såkalte Kempe-kjeder finnes fremdeles i dag i dataassisterte bevis. Imidlertid var Kempes bevis feil, slik Percy Heawood fant elleve år etter publiseringen. Beviset er basert på en induksjon på antall noder i grafen.

Først kan det fastslås at bare trianguleringer trenger å bli observert. Ellers kan vi legge til kanter uten å definere nye noder. Dermed øker fargenes kompleksitet ved å legge til kantene. Hvis denne trianguleringen kan være firefarget, er det også den underliggende grafen. Uten tap av generalitet antar vi altså at grafen som skal farges er triangulert. ${\ displaystyle G}$

I følge en konklusjon fra Eulers teorem er det alltid en node i plane grafer hvis grad er mindre enn eller lik fem, dvs. har maksimalt fem naboer. Vi fjerner denne noden i første trinn og fargelegger grafen med fire farger, noe som er mulig i henhold til induksjonshypotesen. Følgende tre tilfeller kan nå forekomme for noder etter at de er satt inn: ${\ displaystyle v}$ ${\ displaystyle G \ setminus v}$ ${\ displaystyle v}$

${\ displaystyle v}$ har tre eller færre naboer. I dette tilfellet er det en av de fire fargene som uansett er igjen, siden maksimalt tre farger kan brukes i nabolaget. ${\ displaystyle v}$
${\ displaystyle v}$ har fire naboer. Det kan antas at disse er farget i fire forskjellige farger, ellers 1. gå til sak, vi antar at nodene og ikke rødgrønne av en kjede er koblet sammen, vi kan grønne og fargen rød i komponenten av byttet. Så vi fargelegger alle nodene som ligger på en bane i grafen som starter i og bare bruker røde eller grønne noder. Etter denne prosedyren er knuten rød. Siden det ikke lenger er en grønn node i nærheten av , kan den farges grønt. Ellers må det være en kjede mellom og (se skisse 2). I følge Jordans kursetekst kan det imidlertid ikke være en annen kjede mellom og . Dette betyr er isolert av den rødgrønne kjeden fra . Dermed, med analogt resonnement, kan fargene blå og gul byttes ut i undergrafen som inneholder. Følgelig kan den farges i blått. ${\ displaystyle v_ {1}}$ ${\ displaystyle v_ {3}}$ ${\ displaystyle v_ {1}}$ ${\ displaystyle G}$ ${\ displaystyle v_ {1}}$ ${\ displaystyle v_ {1}}$ ${\ displaystyle v}$ ${\ displaystyle v_ {1}}$ ${\ displaystyle v_ {3}}$ ${\ displaystyle v_ {2}}$ ${\ displaystyle v_ {4}}$ ${\ displaystyle v_ {2}}$ ${\ displaystyle v_ {4}}$ ${\ displaystyle v_ {2}}$ ${\ displaystyle v}$
${\ displaystyle v}$ har fem naboer med fire farger. Igjen brukes Kempe-kjeder. Med en prosedyre som er analog med tilfelle 2, er det kjeder fra til og . Ellers, og komponenten som er festet til den, kan være farget blå eller gul, noe som vil gjøre fargen rød gratis. Imidlertid vil noden være fra isolert. Dette lar deg farge i gult uten å endre fargen. Også er av isolert og dette fører bladene blir blå, uten fargestoffer til endringen. Oppsummert har fargen grønn blitt slettet fra nabolaget til , slik at den kan farges grønt. ${\ displaystyle v_ {1}}$ ${\ displaystyle v_ {3}}$ ${\ displaystyle v_ {4}}$ ${\ displaystyle v_ {1}}$ ${\ displaystyle v}$ ${\ displaystyle v_ {2}}$ ${\ displaystyle v_ {4}}$ ${\ displaystyle v_ {2}}$ ${\ displaystyle v_ {4}}$ ${\ displaystyle v_ {5}}$ ${\ displaystyle v_ {3}}$ ${\ displaystyle v_ {5}}$ ${\ displaystyle v_ {3}}$ ${\ displaystyle v}$

I alle fall kan det finnes en farge på knuten , som avslutter induksjonssikkerheten. ${\ displaystyle v}$

Feil i bevis

Errera-graf med Kempe-kjeder
Errera-graf med ødelagte Kempe-kjeder etter et fargeskifte

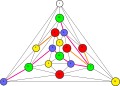
Kempe overså det faktum at endring av fargen på en komponent kan skade isolasjonskjeden til den andre komponenten. Errera-grafen fungerer som et eksempel (se grafikk til høyre). Vi får en feilfri induktiv farging etter Kempes metode opp til node 1. Her er vi i ovennevnte tilfelle 3, så node 1 har fem naboer i fire farger. Vi observerer også Kempe-kjedene som nettopp ble presentert (rødblå fra node 5 til 17, rødgul fra node 3 til 17, se skisse Errera-graf). De to grønne naboene er isolerte. I dette tilfellet er node 12 skilt fra gul node 3. I følge Kempe-metoden blir node 12 således farget gul, som også endrer fargen på node 7 i nærheten, noe som gjør den grønn. Denne omfargingen av knute 7 bryter nå den andre beskyttende rødgule kjeden. Node 10 er nå ikke lenger isolert fra node 5, og det opprettes en grønnblå kjede mellom disse to. Så det er ikke mulig å omfarge node 10 uten å endre fargen på node 5. Så vi er i samme situasjon som i begynnelsen, node 1 har fem naboer i fire farger, med fargen gul som nå vises to ganger. Som et resultat kunne ingen farger tømmes for. Metoden mislykkes. ${\ displaystyle v}$

Feilaktig bevis og moteksempler

Dette kortet er farget i fem farger, og du må ...
... farg minst fire av de ti regionene for å gjøre det med bare fire farger.

Som mange åpne problemer i matematikk, har firefargesetningen provosert mange feil bevis og moteksempler. Det ble forsøkt å konstruere kort som et moteksempel til firefargesettet. Noen av disse konstruksjonene tålte offentlig gransking i flere tiår til de ble anerkjent som feil. Mange flere, hovedsakelig utviklet av amatører, har aldri blitt publisert.

De enkleste "moteksemplene" inneholder ofte en region som berører alle andre regioner. Dette tvinger alle andre regioner til å være trefargede for å sikre at hele kartet kan være firefarget. Moteksemplene overser det faktum at dette kan oppnås ved å endre fargen på det indre området, siden de lener seg for mye på det ytre området.

Dette trikset kan generaliseres; det er enkelt å lage kart som det er umulig å komme seg forbi med fire farger hvis fargene i noen regioner er bestemt på forhånd. En kortvarig kontrollør av moteksemplet vil ofte ikke tenke på å gjenopprette disse regionene.

Andre falske motbeviser bryter med antagelsen om teoremet, for eksempel ved å bruke regioner som består av flere separate områder, eller ved å forby regioner med samme farge som bare berører på et tidspunkt.

Generaliseringer

Kart på en torus som krever syv farger
Kart vist med 7 farger i flyet
Animert torus av samme kart

Firefarget problemet er et spesielt tilfelle av Heawood-formodningen . Det klassiske firefargede problemet gjelder kart som ligger på et plan eller sfærisk overflate. Heawood-formodningen stiller det samme spørsmålet for generelle overflater, som Klein-flasken (6 farger), Möbius-stripen (6 farger), det projiserende planet (6 farger) og torusen (7 farger). Interessant er generaliseringen - bortsett fra det spesielle tilfellet for fly eller sfæriske overflater - mye lettere å bevise enn firefarget teoremet og krever ikke en datamaskin. J. W. Ted Youngs og Gerhard Ringel var i stand til å bevise Heawood-formodningen for alle andre saker for første gang i 1968 ( Ringel-Youngs teorem ). Fire-fargesetningen bekreftes derfor ikke av dette beviset, men må behandles separat.

For lukkede, orienterbare eller ikke-orienterbare flater med positivt kjønn , avhenger det maksimale antall farger som kreves av overflaten Euler og er ${\ displaystyle n}$ ${\ displaystyle \ chi}$

{\ displaystyle n = \ left \ lfloor {\ frac {7 + {\ sqrt {49-24 \ chi}}} {2}} \ right \ rfloor}

hvor parentesene angir avrundingsfunksjonen .

Alternativt kan antall farger spesifiseres for orienterbare overflater avhengig av overflatens kjønn : ${\ displaystyle n}$ ${\ displaystyle g}$

{\ displaystyle n = \ left \ lfloor {\ frac {7 + {\ sqrt {1 + 48g}}} {2}} \ right \ rfloor}

Etter å ha blitt med i grafikken til høyre, er de to "stolpene" i samme farge koblet sammen og danner hver en (L- eller X-formet) kropp. Siden hver kropp berører hverandre, trenger du like mange farger som søyler (her 8) for farging.

Hvis man utvider oppgaven med det firefarges sett med overflater til et tredimensjonalt euklidisk rom, så er det ingen øvre grense for antall farger. I stedet for "landene" vises tredimensjonale områder ("kropper"), som skal ha forskjellige farger hvis de har et felles grensesnitt. Et eksempel kan konstrueres for hvert nummer ( Heinrich Tietze ) som krever minst farger. Tenk deg "lange" kongruente kuboider ("søyler") som ligger ved siden av hverandre, som sammen danner en kuboid med en kvadratisk base. Deretter er det igjen kuboider som er kongruente til den første ved siden av hverandre, men vinkelrett på de nedre, slik at alle de nedre kuboidene berører alle de øvre kuboidene. Nå er hver av de nedre koblet til nøyaktig en av de øvre, slik at begge sammen danner en kropp på tvers . Hver av disse kroppene berører hverandre; Så du trenger farger, og du har alt du vil . ${\ displaystyle n}$ ${\ displaystyle n}$ ${\ displaystyle n}$ ${\ displaystyle n}$ ${\ displaystyle n}$ ${\ displaystyle n}$

kommentar

Kuratowski-mindreårige
De ${\ displaystyle K_ {5}}$
og ${\ displaystyle K_ {3,3}}$

Hvis et land (som ofte er tilfelle i virkeligheten) er fordelt på flere ikke sammenhengende områder ( kolonier , eksklaver , ...), er ikke den tilknyttede grafen nødvendigvis plan og mer enn fire farger kan være nødvendig for farging. Gitte grafer kan testes veldig raskt for planaritet. I følge Kuratowskis teorem er det visse underbilder som forhindrer at grafer blir plane. Det er nøyaktig to grunnleggende former, de såkalte Kuratowski mindreårige og , og deres underavdelinger. Med et dyktig valg av datastrukturene kan man finne disse "undergrafene" eller bestemme at de ikke eksisterer ved å betrakte hver node og hver kant bare et konstant antall ganger. ${\ displaystyle K_ {5}}$ ${\ displaystyle K_ {3,3}}$

Å finne den minste mulige fargen i generelle grafer , med andre ord å bestemme det såkalte kromatiske tallet , er en veldig kompleks oppgave (nærmere bestemt: i sin beslutningsvariant NP-komplett ). I følge Tutte ville det bli løst hvis en minste gruppe ble funnet i den doble grafen , slik at en gruppevurdert strøm (det vil si en " strøm uten begynnelse og slutt") som ikke antar null-elementet noe sted. Denne gruppeordren kalles flytenummeret og er for hvilken som helst graf . Løseligheten av dette fortsatt NP-komplette problemet er uavhengig av strukturen til den gitte gruppen og avhenger bare av gruppeordren. ${\ displaystyle G}$ ${\ displaystyle \ chi (G)}$ ${\ displaystyle G ^ {*}}$ ${\ displaystyle \ varphi (G ^ {*})}$ ${\ displaystyle \ varphi (G ^ {*}) = \ chi (G)}$

Det er ytterligere sammenhenger mellom firefargeproblemet og problemene i diskret matematikk , slik at metoder for algebraisk topologi også kan brukes.

Tidskompleksitet

Å beregne en 4- farging er mulig for plane grafer med noder i tide . I motsetning er avgjørelsen om tre farger er tilstrekkelig NP-komplett . ${\ displaystyle n}$ ${\ displaystyle O (n ^ {2})}$

litteratur

Neil Robertson, Daniel P. Sanders, Paul Seymour, Robin Thomas: Et nytt bevis på firefargesetningen. I: Electronic Research Announcements of the American Mathematical Society . 2/1996. Pp. 17-25.
Kenneth Appel, Wolfgang Haken: Hvert plankart er fire fargelagt. I: Contemp. Matematikk Vol. 98, Amer. Math. Soc., Providence, RI, 1989.
Georges Gonthier: Et datamaskinkontrollert bevis på Four Color Theorem (PDF; 607 kB). upublisert, på denne Gonthier: Formal proof- the four color theorem , Notices AMS 2008 (PDF).
Rudolf Fritsch , Gerda Fritsch: Firefargesetningen: historie, topologiske grunnlag og bevis på bevis. BI-Wissenschaftsverlag, 2004, ISBN 3-411-15141-2 ( PDF ).
Robin Thomas: En oppdatering om setningen med fire farger. Merknader AMS 1998, utgave 7 ( PDF ).
Gerhard Ringel : Kortet fargelegging problem . I: Selecta Mathematica III (red. Konrad Jacobs) (= Heidelberger Taschenbücher . Volum 86 ). Springer Verlag , Berlin, Heidelberg, New York 1971, ISBN 3-540-05333-6 ( MR0543809 ).
Ian Stewart: The Final Riddles of Mathematics . 2. utgave. Rowohlt Taschenbuch Verlag , Reinbek bei Hamburg 2015, ISBN 978-3-499-61694-5 .
Lutz Volkmann : Grunnlaget for grafteorien . Springer Verlag, Wien, New York 1996, ISBN 3-211-82774-9 ( MR1392955 ).
Robin Wilson Fire farger er tilstrekkelig. Princeton University Press 2002, Review in AMS Notices, 2004, PDF-fil

weblenker

Commons : sett med fire farger - samling av bilder, videoer og lydfiler

Oppsummering av bevisene fra Robertson, Sanders, Seymour, Thomas på Robin Thomas 'hjemmeside
Simon Tathams Portable Puzzle Collection The Map- spillet dekker temaet.
Omformulering av kartfargesetningen av Louis H. Kauffman (PDF; 589 kB). Omformulering av firefargeproblemet med tanke på George Spencer-Browns tilnærming i formsloven

Individuelle bevis

↑ ^a^b Robin Wilson [2002]: Four Colors Suffice (= Princeton Science Library). Princeton University Press, Princeton, NJ 2014, ISBN 978-0-691-15822-8 .
^ Gary Chartrand, Linda Lesniak: Grafer og graver . CRC Press, 2005, s. 221.
↑ Kenneth Appel, Wolfgang Haken (med samarbeid fra J. Koch): Hvert plankart er firefarget . I: Moderne matematikk . teip 98 . American Mathematical Society, Providence, RI 1989, ISBN 0-8218-5103-9 , doi : 10.1090 / conm / 098 .
^ ^A^b Neil Robertson, Daniel P. Sanders, Paul Seymour, Robin Thomas: Effektivt fire fargeleggende plane grafer . I: ACM Press (Red.): STOC'96: Proceedings of the eight-eight annual ACM symposium on Theory of computing . 1996, s. 571-575. doi : 10.1145 / 237814.238005 .
^ Georges Gonthier: Formal Proof - The Four-Color Theorem . I: Notices of the American Mathematical Society . 55, nr. 11, 2008, s. 1382-1393.
↑ Lutz Volkmann: Grunnlaget for grafteorien. 1996, s. 254-255.
↑ Ian Stewart: The Final Riddles of Mathematics. 2015, s. 131-136.
↑ Født: Minner fra Hermann Minkowski ved retur av 50-årsjubileet for hans død. Die Naturwissenschaften, bind 46, 1959, s. 501
^ Melvin Fitting: The Four Color Theorem. Lehman College, CUNY
^ Wolfram MathWorld: Map Coloring
↑ Christoph Joachim Scriba , Peter Schreiber: 5000 år med geometri. 2. utgave. Springer, Berlin 2005, ISBN 3-540-22471-8 , s. 454 og fig. 7.8.3
↑ Ytterligere uttalelser og setninger om dette i Reinhard Diestel : Graph Theory. Springer, 2000, ISBN 0-387-98976-5 , s. 157 ff.
↑ Michael R. Garey, David S. Johnson: Datamaskiner og intraherbarhet - En guide til teorien om NP-fullstendighet. WH Freeman, 1979. ISBN 0-7167-1045-5 , s. 87ff.

[Wilson-1] Robin Wilson [2002]: Four Colors Suffice (= Princeton Science Library). Princeton University Press, Princeton, NJ 2014, ISBN 978-0-691-15822-8 .

[2] Gary Chartrand, Linda Lesniak: Grafer og graver . CRC Press, 2005, s. 221.

[3] Kenneth Appel, Wolfgang Haken (med samarbeid fra J. Koch): Hvert plankart er firefarget . I: Moderne matematikk . teip 98 . American Mathematical Society, Providence, RI 1989, ISBN 0-8218-5103-9 , doi : 10.1090 / conm / 098 .

[RSST96-4] A^b Neil Robertson, Daniel P. Sanders, Paul Seymour, Robin Thomas: Effektivt fire fargeleggende plane grafer . I: ACM Press (Red.): STOC'96: Proceedings of the eight-eight annual ACM symposium on Theory of computing . 1996, s. 571-575. doi : 10.1145 / 237814.238005 .

[5] Georges Gonthier: Formal Proof - The Four-Color Theorem . I: Notices of the American Mathematical Society . 55, nr. 11, 2008, s. 1382-1393.

[LV-1-6] Lutz Volkmann: Grunnlaget for grafteorien. 1996, s. 254-255.

[IS-1-7] Ian Stewart: The Final Riddles of Mathematics. 2015, s. 131-136.

[8] Født: Minner fra Hermann Minkowski ved retur av 50-årsjubileet for hans død. Die Naturwissenschaften, bind 46, 1959, s. 501

[9] Melvin Fitting: The Four Color Theorem. Lehman College, CUNY

[10] Wolfram MathWorld: Map Coloring

[11] Christoph Joachim Scriba , Peter Schreiber: 5000 år med geometri. 2. utgave. Springer, Berlin 2005, ISBN 3-540-22471-8 , s. 454 og fig. 7.8.3

[12] Ytterligere uttalelser og setninger om dette i Reinhard Diestel : Graph Theory. Springer, 2000, ISBN 0-387-98976-5 , s. 157 ff.

[13] Michael R. Garey, David S. Johnson: Datamaskiner og intraherbarhet - En guide til teorien om NP-fullstendighet. WH Freeman, 1979. ISBN 0-7167-1045-5 , s. 87ff.

Languages