Metode for minste kvadrater

De minste kvadraters metode (korte MKQ eller engelsk minste kvadraters metode , eller bare etter minste kvadraters korte: LS , for å avgrense utvidelser avledet derfra, så som generaliserte minste kvadraters metode , eller den to-trinns fremgangsmåte for minste kvadraters også kalt "vanlig" med tillegg, at vanlige minste kvadrater ( engelsk vanlige minste kvadrater , kort sagt: OLS )), eller KQ-metode (avviklet metode med minste avvikssum av kvadrater ) er de matematiske standardprosedyrene for justering . I dette tilfellet, til et sett med datapunkter , bestemmer en funksjon kjøringen så nær som mulig datapunktene og dermed best mulig oppsummering av dataene. Den hyppigst brukte funksjonen er den rette linjen , som deretter kalles fit line . For å kunne bruke metoden, må funksjonen inneholde minst en parameter . Disse parametrene blir deretter bestemt av metoden slik at når funksjonen sammenlignes med datapunktene og avstanden mellom funksjonsverdien og datapunktet er kvadrat, er summen av disse kvadratiske avstandene så liten som mulig. Avstandene kalles da rester .

Vanligvis brukes denne metoden til å undersøke reelle data, for eksempel fysiske eller økonomiske måleverdier . Disse dataene inneholder ofte uunngåelige målefeil og svingninger . Med forutsetningen om at de målte verdiene er nær de underliggende ” sanne verdiene ” og at det er en viss sammenheng mellom de målte verdiene, kan metoden brukes til å finne en funksjon som beskriver dette forholdet til dataene så godt som mulig . Metoden kan også brukes i revers for å teste forskjellige funksjoner og derved beskrive et ukjent forhold i dataene.

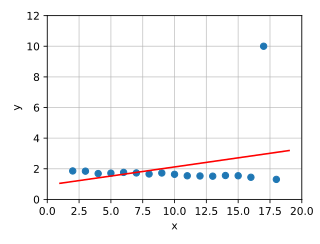
I eksemplet på grafikken er datapunkter og en kompensasjonsfunksjon angitt. Det velges en generell funksjon ( modellfunksjonen ) som skal samsvare med spørsmålet og dataene, i dette tilfellet en logistikkfunksjon . Parametrene deres bestemmes nå på en slik måte at summen av kvadratiske avvik fra observasjonene fra verdiene til funksjonen blir minimert . I grafikken kan avviket på det punktet sees på som en vertikal avstand mellom observasjonen og kurven. ${\ displaystyle e}$${\ displaystyle y}$${\ displaystyle e}$${\ displaystyle x}$${\ displaystyle y}$

I stokastikk brukes metoden med minste kvadrat for det meste som en beregningsmetode for regresjonsanalyse , der den også blir referert til som estimering av minste kvadrat eller vanlig estimering av minste kvadrat . Siden estimeringen av minste kvadrater, restsummen minimert, er det estimeringsmetoden som består av bestemmelse maksimert. Metoden med minste firkanter brukes som systemidentifikasjon i forbindelse med modelleksperimenter f.eks. B. for ingeniører en vei ut av den paradoksale situasjonen med å bestemme modellparametere for ukjente lover.

historie

Første nyttårsdag 1801 oppdaget den italienske astronomen Giuseppe Piazzi dvergplaneten Ceres . Han var i stand til å følge stien i 40 dager, så forsvant Ceres bak solen. I løpet av året, er mange forskere forsøkt uten hell å beregne bane på basis av Piazzi observasjoner - forutsatt at en sirkulær bane, fordi ved den tiden bane elementene bare kan matematisk bestemt fra observerte sky posisjoner for slike .

Den 24 år gamle Gauss klarte å beregne bane ved hjelp av en ny indirekte metode for å bestemme bane og kompensasjonsberegningene hans basert på metoden for minste firkanter (selv om de ennå ikke er utpekt) på en slik måte at Franz Xaver von Zach fant ham 7. desember 1801 og - bekreftet - 31. desember 1801. Heinrich Wilhelm Olbers bekreftet dette uavhengig av Zach gjennom observasjon 1. og 2. januar 1802.

Problemet med å finne Ceres som sådan lå i det faktum at verken plasseringen, en del av stien eller avstanden er kjent fra observasjonene , bare retningen for observasjonen. Dette fører til jakten på en ellipse og ikke etter en sirkel som Gauss konkurrenter antyder. Et av fokuspunktene til ellipsen er kjent ( solen selv), og buene til Ceres bane mellom observasjonsretningene krysses i henhold til Keplers andre lov , det vil si at tidene oppfører seg som overflatene feid av føringsbjelke. I tillegg er det kjent for den beregningsmessige løsningen at observasjonene i seg selv antar en konisk seksjon i rommet, jordens bane i seg selv.

I prinsippet fører problemet til en ligning av åttende grad, hvis trivielle løsning er selve jordens bane. Gjennom omfattende sekundære forhold og (senere) metoden for minste firkanter utviklet av Gauss, klarte 24-åringen å spesifisere plasseringen han hadde beregnet for banen til Ceres for 25. november til 31. desember 1801. Dette gjorde Zach i stand til å finne Ceres på den siste dagen i prognosen. Stedet var ikke mindre enn 7 ° (dvs. 13,5  fullmånebredder ) øst for der de andre astronomene hadde mistenkt Ceres, som ikke bare Zach, men også Olbers behørig hyllet.

Hans første beregninger var fortsatt uten metoden for minste kvadrat , bare når mange nye data ble tilgjengelig etter gjenoppdagelsen av Ceres, brukte han dem for en mer presis bestemmelse av banelementene, men uten å offentliggjøre detaljer om metoden hans. Piazzis rykte, som hadde lidd alvorlig på grunn av banepunktene som ikke ønsket å passe en sirkelsti, ble også gjenopprettet.

En forgjengermetode for metoden med minste kvadrat er metoden for minste absolutte avvik , som ble utviklet i 1760 av Rugjer Josip Bošković . Gauss hadde utviklet det grunnleggende om metoden med minste firkanter allerede i 1795 i en alder av 18 år. Det var basert på en idé av Pierre-Simon Laplace om å legge sammen avvikene fra de målte verdiene fra den forventede verdien på en slik måte at summen av alle disse såkalte feilene resulterte i null. I motsetning til denne metoden brukte Gauss feilkvadratene i stedet for feilene og klarte dermed å dispensere med nullsumkravet. Uavhengig av Gauss utviklet franskmannen Adrien-Marie Legendre den samme metoden, publiserte den først i 1805, på slutten av et lite arbeid med beregning av kometbaner, og publiserte en annen avhandling om den i 1810. Presentasjonen var ekstremt klar og enkelt. Legendre ga også navnet Méthode des moindres carrés (metoden for de minste kvadratene).

I 1809, i det andre bindet av hans himmelske mekaniske verk Theoria motus corporum coelestium in sectionibus conicis solem ambientium (teori om himmelenes bevegelse, som dreier seg om solen i koniske seksjoner) , ga Gauss ut metoden inkludert de normale ligningene, så vel som den Gaussiske eliminasjonsmetoden og Gauss-Newton-metoden , som gikk langt utover Legendre. I den refererte han til minste kvadratmetoden som sin oppdagelse og hevdet å ha oppdaget og anvendt den så tidlig som 1795 (dvs. før Legendre), noe som irriterte ham i lang tid. Legendre klaget over dette i et langt brev til Gauss, som Gauss etterlot ubesvart. Gauss refererte bare innimellom til en oppføring i sin matematiske dagbok fra 17. juni 1798 (det er den kryptiske setningen på latin: Calculus probabilitatis contra La Place defensus (calculus of probability forsvaret mot Laplace) og ingenting annet). Laplace bedømte saken på en slik måte at Legendre gjorde den første publikasjonen, men Gauss kjente utvilsomt metoden på forhånd, brukte den selv og kommuniserte den også til andre astronomer per brev. Metoden med minste kvadrat ble raskt standardmetoden for håndtering av astronomiske eller geodetiske datasett etter publiseringen.

Gauss brukte metoden intenst i sin undersøkelse av kongedømmet Hannover ved triangulering . Det todelte arbeidet ble utgitt i 1821 og 1823, og i 1826 et supplement til Theoria combinedis observationum erroribus minimis obnoxiae (teori om kombinasjonen av observasjoner underlagt de minste feilene) , der Gauss rettferdiggjorde suksessen med metoden med minste kvadrat det faktum at det ble sammenlignet med andre metoder, er justeringsberegningen optimal i bred forstand. Den matematiske formuleringen av denne påstanden er kjent som teoremet til Gauss-Markow , oppkalt etter Andrei Andrejewitsch Markow , som gjenoppdaget og gjorde populær denne delen av Gauss arbeid, som opprinnelig ble neglisjert, i det 20. århundre (se også setning Gauß-Markow. # Geschichte ). Den Theoria Combinationis inneholder også fremgangsmåter for effektivt å løse lineære systemer av ligninger , så som Gauss-Seidel-metoden og LR nedbryting , noe som representerer et betydelig fremskritt på den matematiske kjennskap til tiden.

Den franske oppmålingsoffiser André-Louis Cholesky utviklet Cholesky-spaltningen under første verdenskrig , som igjen representerte en betydelig gevinst i effektivitet sammenlignet med Gauss løsningsmetode. På 1960-tallet utviklet Gene Golub ideen om å løse de forekommende lineære ligningssystemene ved hjelp av QR-dekomponering .

Prosedyren

krav

Man ser på en avhengig variabel som er påvirket av en eller flere variabler. Forlengelsen av en fjær avhenger bare av kraften som brukes, men lønnsomheten til et selskap avhenger av flere faktorer som salg , ulike kostnader eller egenkapital . For å forenkle notasjonen er representasjonen begrenset til en variabel i det følgende . Forholdet mellom og variablene bestemmes av en modellfunksjon , for eksempel en parabel eller en eksponensiell funksjon${\ displaystyle y}$${\ displaystyle x}$${\ displaystyle x}$${\ displaystyle y}$${\ displaystyle f}$

${\ displaystyle y (x) = f (x; \ alpha _ {1}, \ dotsc, \ alpha _ {m})}$,

som avhenger av og av funksjonelle parametere. Denne funksjonen kommer enten fra brukerens kunnskap eller fra et mer eller mindre tidkrevende søk etter en modell. Det kan hende at ulike modellfunksjoner må brukes og resultatene sammenlignes. En enkel sak basert på eksisterende kunnskap er for eksempel fjæren, fordi her er Hookes lov og dermed en lineær funksjon med fjærkonstanten som eneste parameter et modellkrav. Imidlertid, i vanskeligere tilfeller som for selskapet, må valget av funksjonstype innledes med en kompleks modelleringsprosess . ${\ displaystyle x}$${\ displaystyle m}$${\ displaystyle \ alpha _ {j}}$

For å få informasjon om parametrene og dermed den spesifikke forholdet, samles tilsvarende observasjonsverdier for de respektive gitte verdiene til de uavhengige variablene . Parametrene brukes til å tilpasse den valgte funksjonstypen til disse observerte verdiene . Målet er nå å velge parametrene slik at modellfunksjonen tilnærmer seg dataene best mulig. ${\ displaystyle n}$${\ displaystyle x_ {i}}$${\ displaystyle x}$${\ displaystyle y_ {i}}$ ${\ displaystyle (i = 1, \ dotsc, n)}$${\ displaystyle \ alpha _ {j}}$${\ displaystyle y_ {i}}$${\ displaystyle \ alpha _ {j}}$

Gauss og Legendre hadde ideen om å gjøre distribusjonsantagelser om målefeilene til disse observasjonsverdiene. De skal være null i gjennomsnitt, ha en konstant varians og være stokastisk uavhengige av andre målefeil . Dette betyr at det ikke lenger er systematisk informasjon i målefeilene, dvs. at de svinger rundt null rent tilfeldig. I tillegg bør målefeilene fordeles normalt , noe som på den ene siden har sannsynlige fordeler og på den andre siden garanterer at avvikere er så gode som ekskluderte. ${\ displaystyle y}$

For å bestemme parametrene under disse forutsetningene er det generelt nødvendig at det er betydelig flere datapunkter enn parametere, så det må gjelde. ${\ displaystyle \ alpha _ {j}}$${\ displaystyle n> m}$

Minimere summen av kvadratene av feil

Kriteriet for å bestemme tilnærmingen bør velges slik at store avvik fra modellfunksjonen fra dataene vektes tyngre enn små. Hvis ingen løsning er mulig uten avvik, er kompromisset med det minste minste avviket det beste generelt anvendelige kriteriet.

For dette formålet er summen av kvadratene til feilene, som også kalles summen av kvadratene til feilen (mer presist: summen av kvadratene til restene ), som summen av kvadratforskjellene mellom verdier av modellkurven og dataene . ${\ displaystyle f (x_ {i})}$${\ displaystyle y_ {i}}$

I formelnotasjon med parametere og resultater ${\ displaystyle {\ vec {\ alpha}} = (\ alpha _ {1}, \ alpha _ {2}, \ dots, \ alpha _ {m}) \ in \ mathbb {R} ^ {m}}$${\ displaystyle {\ vec {f}} = (f (x_ {1}, {\ vec {\ alpha}}), \ prikker, f (x_ {n}, {\ vec {\ alpha}})) \ i \ mathbb {R} ^ {n}}$

${\ displaystyle \ sum _ {i = 1} ^ {n} (f (x_ {i}, {\ vec {\ alpha}}) - y_ {i}) ^ {2} = \ | {\ vec {f }} - {\ vec {y}} \ | _ {2} ^ {2}.}$

Deretter skal disse parametrene velges som summen av de kvadratiske justeringsfeilene er minimal for: ${\ displaystyle \ alpha _ {j}}$

${\ displaystyle \ min _ {\ vec {\ alpha}} \ | {\ vec {f}} - {\ vec {y}} \ | _ {2} ^ {2}.}$

Hvor nøyaktig dette minimeringsproblemet løses, avhenger av typen modellfunksjon.

Hvis feilsummen av kvadrater forutsies for et eksternt datasett, snakker man om PRESS-statistikken ( engelsk prediktiv restsum av kvadrater ).

Lineær modellfunksjon

Lineære modellfunksjoner er lineære kombinasjoner av vilkårlige, generelt ikke-lineære basisfunksjoner. For slike modellfunksjoner kan minimeringsproblemet også løses analytisk ved hjelp av en ekstrem verditilnærming uten iterative tilnærmingstrinn. Først vises noen enkle spesielle tilfeller og eksempler.

Spesielt tilfelle av en enkel lineær best-fit rett linje

Utledning og prosedyre

Første ordens polynom er en enkel modellfunksjon med to lineære parametere

${\ displaystyle f (x) = \ alpha _ {0} + \ alpha _ {1} x}$

Vi ser etter koeffisientene og den best passende linjen for de gitte måleverdiene . Avvikene mellom den rette linjen du leter etter og de respektive måleverdiene ${\ displaystyle n}$${\ displaystyle (x_ {1}, y_ {1}), \ dotsc, (x_ {n}, y_ {n})}$${\ displaystyle \ alpha _ {0}}$${\ displaystyle \ alpha _ {1}}$${\ displaystyle r_ {i}}$

${\ displaystyle {\ begin {matrix} r_ {1} = & \ alpha _ {0} + & \ alpha _ {1} x_ {1} -y_ {1} \\ r_ {2} = & \ alpha _ { 0} + & \ alpha _ {1} x_ {2} -y_ {2} \\\ vdots & \ vdots & \ vdots \\ r_ {n} = & \ alpha _ {0} + & \ alpha _ {1 } x_ {n} -y_ {n} \\\ slutt {matrise}}}$

kalles tilpasningsfeil eller rester . Vi leter nå etter koeffisientene og med den minste summen av kvadratene av feilene ${\ displaystyle \ alpha _ {0}}$${\ displaystyle \ alpha _ {1}}$

${\ displaystyle \ min _ {\ alpha _ {0}, \ alpha _ {1}} \ sum _ {i = 1} ^ {n} r_ {i} ^ {2}}$.

Den store fordelen med tilnærmingen med denne firkanten av feilene blir synlig når denne minimeringen utføres matematisk: Sumfunksjonen forstås som en funksjon av de to variablene og (de innkommende måleverdiene er numeriske konstanter), deretter den deriverte (mer presist: delderivater ) av Funksjonen basert på disse variablene (dvs. og ) og til slutt søkte etter nullpunktet fra denne avledningen . Resultatet er det lineære ligningssystemet${\ displaystyle \ alpha _ {0}}$${\ displaystyle \ alpha _ {1}}$${\ displaystyle \ alpha _ {0}}$${\ displaystyle \ alpha _ {1}}$

${\ displaystyle {\ begin {align} \ textstyle n \ cdot \ alpha _ {0} + \ left (\ sum \ limits _ {i = 1} ^ {n} x_ {i} \ right) \ alpha _ {1 } & = \ textstyle \ sum \ limits _ {i = 1} ^ {n} y_ {i} \\\ textstyle \ left (\ sum \ limits _ {i = 1} ^ {n} x_ {i} \ right ) \ alpha _ {0} + \ left (\ sum \ limits _ {i = 1} ^ {n} x_ {i} ^ {2} \ right) \ alpha _ {1} & = \ textstyle \ sum \ limits _ {i = 1} ^ {n} x_ {i} y_ {i} \ end {justert}}}$

med løsningen

${\ displaystyle \ alpha _ {1} = {\ frac {\ sum \ nolimits _ {i = 1} ^ {n} (x_ {i} - {\ overline {x}}) y_ {i}} {\ sum \ nolimits _ {i = 1} ^ {n} (x_ {i} - {\ overline {x}}) ^ {2}}} = {\ frac {\ sum \ nolimits _ {i = 1} ^ {n } (x_ {i} - {\ overline {x}}) (y_ {i} - {\ overline {y}})} {\ sum \ nolimits _ {i = 1} ^ {n} (x_ {i} - {\ overline {x}}) ^ {2}}} = {\ frac {SP_ {xy}} {SQ_ {x}}}}$og ,${\ displaystyle \; \ alpha _ {0} = {\ overline {y}} - \ alpha _ {1} {\ overline {x}}}$

hvor betegner den summen av produktene av avvik mellom og , og representerer den summen av de kvadrerte avvik av . Det er det aritmetiske gjennomsnittet av verdiene . Løsningen for kan også bli funnet i usentrert form ved hjelp av forskyvningssetningen${\ displaystyle SP_ {xy}}$${\ displaystyle x}$${\ displaystyle y}$${\ displaystyle SQ_ {x}}$${\ displaystyle x}$${\ displaystyle \ textstyle {\ overline {x}} = {\ frac {1} {n}} \ sum \ nolimits _ {i = 1} ^ {n} x_ {i}}$${\ displaystyle x}$${\ displaystyle {\ overline {y}}}$${\ displaystyle \ alpha _ {1}}$

${\ displaystyle \ alpha _ {1} = {\ frac {\ sum _ {i = 1} ^ {n} (x_ {i} y_ {i}) - n {\ overline {x}} {\ overline {y }}} {\ left (\ sum _ {i = 1} ^ {n} x_ {i} ^ {2} \ right) -n {\ overline {x}} ^ {2}}}}$

kan spesifiseres. Disse resultatene kan også avledes med funksjoner av en reell variabel, dvs. uten partielle derivater.

Eksempel med en best tilpasset rett linje

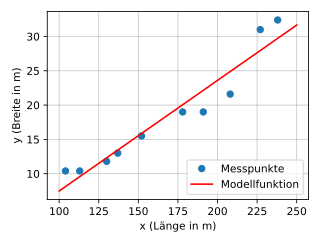
I dette eksemplet beregnes en best tilpasset rett linje av formen for å vise forholdet mellom to funksjoner i et datasett. Datasettet består av lengden og bredden på ti krigsskip (se krigsskipdata ). Det bør gjøres et forsøk på å knytte breddegrad til lengdegrad. Dataene presenteres i de tre første kolonnene i tabellen nedenfor. De andre kolonnene er knyttet til mellomresultater for beregning av den rette linjen. Variabelen skal angi lengden på krigsskipet og bredden. Vi ser etter den rette linjen , hvis funksjonsverdiene er så nær de kjente verdiene , hvis de kjente verdiene brukes . ${\ displaystyle f (x) = \ alpha _ {0} + \ alpha _ {1} x}$${\ displaystyle x_ {i}}$${\ displaystyle i}$${\ displaystyle y_ {i}}$${\ displaystyle f (x) = y = \ alpha _ {0} + \ alpha _ {1} x}$${\ displaystyle x_ {i}}$${\ displaystyle f (x_ {i}) = {\ tilde {y}} _ {i}}$${\ displaystyle y_ {i}}$

Krigsskip	Lengde (m)	Bredde (m)	${\ displaystyle (x_ {i} - {\ overline {x}})}$	${\ displaystyle (y_ {i} - {\ overline {y}})}$
${\ displaystyle i}$	${\ displaystyle x_ {i}}$	${\ displaystyle y_ {i}}$	${\ displaystyle x_ {i} ^ {*}}$	${\ displaystyle y_ {i} ^ {*}}$	${\ displaystyle x_ {i} ^ {*} \ cdot y_ {i} ^ {*}}$	${\ displaystyle (x_ {i} ^ {*}) ^ {2}}$	${\ displaystyle f (x_ {i})}$	${\ displaystyle f (x_ {i}) - y_ {i}}$
1	208	21.6	40.2	3.19	128,24	1616.04	24,88	3.28
2	152	15.5	−15.8	−2.91	45,98	249,64	15.86	0,36
3	113	10.4	−54,8	−8.01	438,95	3003.04	9.57	−0.83
4. plass	227	31.0	59.2	12.59	745,33	3504,64	27,95	−3.05
5	137	13.0	−30.8	−5.41	166,63	948,64	13.44	0,44
Sjette	238	32.4	70.2	13.99	982.10	4928.04	29,72	−2.68
7.	178	19.0	10.2	0,59	6.02	104.04	20.05	1.05
8. plass	104	10.4	−63.8	−8.01	511.04	4070.44	8.12	−2.28
9	191	19.0	23.2	0,59	13.69	538,24	22.14	3.14
10	130	11.8	−37.8	−6.61	249,86	1428,84	12.31	0,51
Sum Σ	1678	184.1			3287,82	20391,60

Den best tilpassede linjen bestemmes av koeffisientene og som beregnes ved å bruke som spesifisert ovenfor ${\ displaystyle \ alpha _ {0}}$${\ displaystyle \ alpha _ {1}}$

${\ displaystyle \ alpha _ {1} = {\ frac {\ sum \ nolimits _ {i = 1} ^ {n} (x_ {i} - {\ overline {x}}) (y_ {i} - {\ overlinje {y}})} {\ sum \ nolimits _ {i = 1} ^ {n} (x_ {i} - {\ overline {x}}) ^ {2}}} = {\ frac {SP_ {xy }} {SQ_ {x}}}}$

${\ displaystyle \ alpha _ {0} = {\ overline {y}} - \ alpha _ {1} {\ overline {x}}}$

Konstantene og er henholdsvis gjennomsnittsverdiene for - og beregninger, så ${\ displaystyle {\ overline {x}}}$${\ displaystyle {\ overline {y}}}$${\ displaystyle x}$${\ displaystyle y}$

${\ displaystyle {\ overline {x}} = {\ frac {\ sum \ nolimits _ {i = 1} ^ {n} x_ {i}} {n}} = {\ frac {1678} {10}} = 167 {,} 8}$

${\ displaystyle {\ overline {y}} = {\ frac {184.1} {10}} = 18 {,} 41}$

Som et første mellomtrinn kan avviket fra gjennomsnittsverdien nå beregnes for hvert krigsskip: og - disse verdiene er angitt i fjerde og femte kolonne i tabellen ovenfor. Dette forenkler formelen for${\ displaystyle x_ {i} ^ {*} = (x_ {i} - {\ overline {x}})}$${\ displaystyle \; y_ {i} ^ {*} = (y_ {i} - {\ overline {y}})}$${\ displaystyle \ alpha _ {1}}$

${\ displaystyle \ alpha _ {1} = {\ frac {\ sum \ nolimits _ {i = 1} ^ {n} x_ {i} ^ {*} \ cdot y_ {i} ^ {*}} {\ sum \ ngrenser _ {i = 1} ^ {n} (x_ {i} ^ {*}) ^ {2}}}}$

Som et andre mellomliggende trinn, produktene og kan beregnes for hver krigsskip. Disse verdiene er lagt inn i den sjette og syvende kolonnen i tabellen og kan nå enkelt legges sammen. Dette kan beregnes som ${\ displaystyle x_ {i} ^ {*} \ cdot y_ {i} ^ {*}}$${\ displaystyle (x_ {i} ^ {*}) ^ {2}}$${\ displaystyle \ alpha _ {1}}$

${\ displaystyle \ alpha _ {1} = {\ frac {3287 {,} 82} {20391 {,} 60}} = 0 {,} 1612}$

Verdien av kan allerede tolkes: Med forutsetningen om at dataene er lineært relaterte og kan beskrives av vår beregnede best-fit linje, øker bredden på et krigsskip med ca. 0,16 meter for hver hele meter som den er lengre er. ${\ displaystyle \ alpha _ {1}}$

Avskjæringen er da ${\ displaystyle \ alpha _ {0}}$

${\ displaystyle \ alpha _ {0} = {\ overline {y}} - \ alpha _ {1} {\ overline {x}} = 18 {,} 41-0 {,} 1612 \ cdot 167 {,} 8 = -8 {,} 6451}$

Ligningen til den best tilpassede linjen er altså ${\ displaystyle f (x) = - 8 {,} 6451 + 0 {,} 1612x}$

For å illustrere dette kan dataene plottes som et spredningsdiagram og den beste linjen settes inn. Grafen antyder at det virkelig er et lineært forhold mellom lengden og bredden på et krigsskip for våre eksempeldata. Justeringen av poengene er ganske bra. Avviket fra verdiene som er spådd av den rette linjen fra de målte verdiene kan også sees på som et mål . De tilsvarende verdiene er angitt i den åttende og niende kolonnen i tabellen. Gjennomsnittlig avvik er 2,1 m. Bestemmelseskoeffisienten , som standardisert koeffisient, gir også en verdi på omtrent 92,2% (100% tilsvarer et gjennomsnittlig avvik på 0 m); for beregningen se eksemplet for bestemmelseskoeffisienten . ${\ displaystyle f (x_ {i}) - y_ {i}}$${\ displaystyle f (x_ {i})}$${\ displaystyle y_ {i}}$

Imidlertid betyr det negative skjæringspunktet at i vår lineære modell har et krigsskip med en lengde på 0 meter en negativ bredde - eller krigsskip begynner bare å eksistere fra en viss minimumslengde. Sammenlignet med virkeligheten er dette selvfølgelig feil, noe som kan tas i betraktning når man vurderer en statistisk analyse. Det er sannsynlig at modellen bare er gyldig for det området de målte verdiene faktisk er tilgjengelige for (i dette tilfellet for krigsskiplengder mellom 100 m og 240 m), og at utenfor linjen er en lineær funksjon ikke lenger egnet til å representere dataen. ${\ displaystyle \ alpha _ {0}}$

Enkle kurver for polynom med best passform

Best-fit polynomer er mer generelle enn en lineær best-fit linje

${\ displaystyle y (x) \ approx \ alpha _ {0} + \ alpha _ {1} x + \ alpha _ {2} x ^ {2} + \ dotsb + \ alpha _ {q} x ^ {q} }$,

som nå vil bli illustrert ved hjelp av et eksempel (slike best egnet polynomiske tilnærminger kan - i tillegg til den iterative løsningen - løses analytisk ved hjelp av en ekstremverditilnærming).

Resultatene av microcensus undersøkelse av Federal Statistical Office er gjennomsnittsvekt av menn etter aldersgruppe (kilde: Federal Statistical Office, Wiesbaden 2009). For analysen ble aldersgruppene erstattet av middelklassen. Avhengigheten av variabel vekt ( ) av variabel alder ( ) skal analyseres. ${\ displaystyle y}$${\ displaystyle x}$

Spredningsdiagrammet antyder et omtrent parabolsk forhold mellom og som ofte kan tilnærmes godt ved hjelp av et polynom. Det blir en polynomisk tilnærming til formen ${\ displaystyle x}$${\ displaystyle y}$

${\ displaystyle y (x) \ approx \ alpha _ {0} + \ alpha _ {1} x + \ alpha _ {2} x ^ {2} + \ alpha _ {3} x ^ {3} + \ alpha _ {4} x ^ {4}}$

prøver. Løsningen er 4. graders polynom

${\ displaystyle y (x) \ approx 47 {,} 86 + 2 {,} 2x-0 {,} 04809x ^ {2} +0 {,} 0004935x ^ {3} -0 {,} 000002148x ^ {4} }$.

Målepunktene avviker i gjennomsnitt ( standardavvik ) 0,19 kg fra modellfunksjonen. Hvis du reduserer graden av polynom til 3, får du løsningen

${\ displaystyle y (x) \ ca 54 {,} 22 + 1 {,} 515x-0 {,} 0226x ^ ​​{2} +0 {,} 0001002x ^ {3}}$

med et gjennomsnittlig avvik på 0,22 kg og med polynomgrad 2 løsningen

${\ displaystyle y (x) \ approx 61 {,} 42 + 0 {,} 9397x-0 {,} 008881x ^ {2}}$

med et gjennomsnittlig avvik på 0,42 kg. Som man kan se, hvis de høyere vilkårene er utelatt, endres koeffisientene til de lavere vilkårene. Metoden prøver å få det beste ut av enhver situasjon. Tilsvarende kompenseres de manglende høyere vilkårene så godt som mulig ved hjelp av de lavere vilkårene til det matematiske optimum er nådd. Andregrads polynom (parabel) beskriver forløpet til målepunktene veldig bra (se figur).

Spesielt tilfelle av en lineær justeringsfunksjon med flere variabler

Hvis modellfunksjonen er et flerdimensjonalt polynom av første orden, dvs. hvis den har flere uavhengige modellvariabler i stedet for bare en variabel , oppnås en lineær funksjon av skjemaet ${\ displaystyle x}$${\ displaystyle x_ {1}, \ ldots, x_ {N}}$

${\ displaystyle f (x_ {1}, \ dotsc, x_ {N}; \ alpha _ {0}, \ alpha _ {1}, \ dotsc, \ alpha _ {N}) = \ alpha _ {0} + \ alpha _ {1} x_ {1} + \ dotsb + \ alpha _ {N} x_ {N}}$,

de på restene

${\ displaystyle {\ begin {matrix} r_ {1} = & \ alpha _ {0} + \ alpha _ {1} x_ {1,1} + & \ dotsb \; \; + \ alpha _ {j} x_ {j, 1} + & \ dotsb \; \; + \ alpha _ {N} x_ {N, 1} -y_ {1} \\ r_ {2} = α _ {0} + \ alpha _ {1} x_ {1,2} + & \ dotsb \; \; + \ alpha _ {j} x_ {j, 2} + & \ dotsb \; \; + \ alpha _ {N} x_ {N, 2} -y_ {2} \\\ vdots & \ vdots & \ vdots & \ vdots \\ r_ {i} = & \ alpha _ {0} + \ alpha _ {1} x_ {1, i} + & \ dotsb \; \ ; + \ alpha _ {j} x_ {j, i} + & \ dotsb \; \; + \ alpha _ {N} x_ {N, i} -y_ {i} \\\ vdots & \ vdots & \ vdots & \ vdots \\ r_ {n} = α _ {0} + \ alpha _ {1} x_ {1, n} + & \ dotsb \; \; + \ alpha _ {j} x_ {j, n} + & \ dotsb \; \; + \ alpha _ {N} x_ {N, n} -y_ {n} \\\ end {matrix}}}$

fører og om minimeringsmetoden

${\ displaystyle \ min _ {\ alpha} \ sum _ {i = 1} ^ {n} r_ {i} ^ {2}}$

kan løses.

Det generelle lineære tilfellet

I det følgende vil det generelle tilfellet for alle lineære modellfunksjoner med en hvilken som helst dimensjon vises. For en gitt måleverdifunksjon

${\ displaystyle y (x_ {1}, x_ {2}, \ prikker, x_ {N})}$

med uavhengige variabler er en optimalt tilpasset lineær modellfunksjon ${\ displaystyle N}$

${\ displaystyle f (x_ {1}, x_ {2}, \ dots, x_ {N}; \ alpha _ {1}, \ alpha _ {2}, \ dots, \ alpha _ {m}) = \ sum _ {j = 1} ^ {m} \ alpha _ {j} \ varphi _ {j} (x_ {1}, x_ {2}, \ prikker, x_ {N})}$

ønsket hvis kvadratiske avvik skulle være minimalt. er funksjonskoordinatene, de lineære innkommende parametrene som skal bestemmes og eventuelle lineært uavhengige funksjoner valgt for tilpasning til problemet. ${\ displaystyle x_ {i}}$${\ displaystyle \ alpha _ {j}}$${\ displaystyle \ varphi _ {j}}$

Ved gitte målepunkter ${\ displaystyle n}$

${\ displaystyle (x_ {1,1}, x_ {2,1}, \ prikker, x_ {N, 1}; y_ {1}), (x_ {1,2}, x_ {2,2}, \ prikker, x_ {N, 2}; y_ {2}), \ prikker, (x_ {1, n}, x_ {2, n}, \ prikker, x_ {N, n}; y_ {n})}$

man får justeringsfeilene

${\ displaystyle {\ begin {matrix} r_ {1} = & \ alpha _ {1} \ varphi _ {1} (x_ {1,1}, \ prikker, x_ {N, 1}) \; \; + α _ {2} \ varphi _ {2} (x_ {1,1}, \ prikker, x_ {N, 1}) + & \ cdots \; \; \; + \ alpha _ {m} \ varphi _ { m} (x_ {1,1}, \ prikker, x_ {N, 1}) - y_ {1} \\ r_ {2} = & \ alpha _ {1} \ varphi _ {1} (x_ {1, 2}, \ prikker, x_ {N, 2}) \; \; + α _ {2} \ varphi _ {2} (x_ {1,2}, \ prikker, x_ {N, 2}) + & \ cdots \; \; \; + \ alpha _ {m} \ varphi _ {m} (x_ {1,2}, \ dots, x_ {N, 2}) - y_ {2} \\\ vdots & \ vdots & \ vdots & \ vdots \\ r_ {i} = & \ alpha _ {1} \ varphi _ {1} (x_ {1, i}, \ prikker, x_ {N, i}) \; \; + α _ {2} \ varphi _ {2} (x_ {1, i}, \ dots, x_ {N, i}) + & \ cdots \; \; \; + \ alpha _ {m} \ varphi _ {m } (x_ {1, i}, \ prikker, x_ {N, i}) - y_ {i} \\\ vdots & \ vdots & \ vdots & \ vdots \\ r_ {n} = & \ alpha _ {1 } \ varphi _ {1} (x_ {1, n}, \ prikker, x_ {N, n}) \; \; + & \ alpha _ {2} \ varphi _ {2} (x_ {1, n} , \ prikker, x_ {N, n}) + & \ cdots \; \; \; + \ alpha _ {m} \ varphi _ {m} (x_ {1, n}, \ prikker, x_ {N, n }) - y_ {n} \\\ slutt {matrise}}}$

eller i matriksnotasjon

${\ displaystyle r = A \ alpha -y,}$

karakterisert ved at vektoren som oppsummerer hvilke matrisebasisfunksjonsverdier , parametervektor , er parametrene og vektoren observasjonene der . ${\ displaystyle r \ in \ mathbb {R} ^ {n}}$${\ displaystyle r_ {i}}$ ${\ displaystyle A \ in \ mathbb {R} ^ {n \ times m}}$${\ displaystyle A_ {ij}: = \ varphi _ {j} (x_ {1, i}, \ prikker, x_ {N, i})}$${\ displaystyle \ alpha \ in \ mathbb {R} ^ {m}}$${\ displaystyle \ alpha _ {j}}$${\ displaystyle y \ in \ mathbb {R} ^ {n}}$${\ displaystyle y_ {i}}$${\ displaystyle n \ geq m}$

Minimeringsproblemet ved bruk av den euklidiske normen ved

${\ displaystyle \ min _ {\ alpha} \ sum _ {i = 1} ^ {n} r_ {i} ^ {2} = \ min _ {\ alpha} \ | f (\ alpha) -y \ | _ {2} ^ {2} = \ min _ {\ alpha} \ | A \ alpha -y \ | _ {2} ^ {2}}$

kan formuleres i vanlig tilfelle (dvs. har full kolonneplassering , så det er vanlig og dermed inverterbar) med formelen ${\ displaystyle A}$${\ displaystyle A ^ {T} A}$

${\ displaystyle \ alpha = (A ^ {T} A) ^ {- 1} A ^ {T} y}$

kan løses tydelig analytisk, som vil bli forklart i neste avsnitt. I entall , hvis ikke er av full rang, kan ikke systemet med normale ligninger løses unikt, dvs. H. parameteren kan ikke identifiseres (se Gauss-Markows teorem # Enkel bokstav, estimerbare funksjoner ). ${\ displaystyle A}$${\ displaystyle \ alpha}$

Løsning av minimeringsproblemet

Utledning og prosedyre

Minimeringsproblemet oppstår, som vist i det generelle lineære tilfellet, som

${\ displaystyle \ min _ {\ alpha} \ | A \ alpha -y \ | _ {2} ^ {2} = \ min _ {\ alpha} (A \ alpha -y) ^ {T} (A \ alpha -y) = \ min _ {\ alpha} (\ alpha ^ {T} A ^ {T} A \ alpha -2y ^ {T} A \ alpha + y ^ {T} y).}$

Dette problemet kan alltid løses. Hvis matrisen har full rang , er løsningen til og med unik. For å bestemme extremal punkt, nullstilling de partielle deriverte med hensyn til , ${\ displaystyle A}$${\ displaystyle \ alpha _ {j}}$

${\ displaystyle \ nabla \ | A \ alpha -y \ | _ {2} ^ {2} = 2 (A \ alpha -y) ^ {T} A,}$

et lineært system med normale ligninger (også Gaussiske normale ligninger eller normale ligninger )

${\ displaystyle A ^ {T} A \ alpha = A ^ {T} y,}$

som gir løsningen på minimeringsproblemet og generelt må løses numerisk. Har full rang og er , matrisen er positiv bestemt, slik at ekstremum funnet er virkelig et minimum. På denne måten kan løsning av minimeringsproblemet reduseres til å løse et ligningssystem. I det enkle tilfellet med en best tilpasset rett linje, kan løsningen, som vist, til og med gis direkte som en enkel formel. ${\ displaystyle A}$${\ displaystyle n \ geq m}$${\ displaystyle A ^ {T} A}$

Alternativt kan de normale ligningene vises i representasjonen

${\ displaystyle A ^ {T} A \ alpha -A ^ {T} y = {\ begin {pmatrix} \ left \ langle \ varphi _ {1}, \ varphi _ {1} \ right \ rangle & \ left \ langle \ varphi _ {1}, \ varphi _ {2} \ right \ rangle & \ cdots & \ left \ langle \ varphi _ {1}, \ varphi _ {m} \ right \ rangle \\\ left \ langle \ varphi _ {2}, \ varphi _ {1} \ right \ rangle & \ left \ langle \ varphi _ {2}, \ varphi _ {2} \ right \ rangle & \ cdots & \ left \ langle \ varphi _ { 2}, \ varphi _ {m} \ right \ rangle \\\ vdots & \ vdots & \ ddots & \ vdots \\\ left \ langle \ varphi _ {m}, \ varphi _ {1} \ right \ rangle & \ left \ langle \ varphi _ {m}, \ varphi _ {2} \ right \ rangle & \ cdots & \ left \ langle \ varphi _ {m}, \ varphi _ {m} \ right \ rangle \\\ end {pmatrix}} {\ begin {pmatrix} \ alpha _ {1} \\\ alpha _ {2} \\\ vdots \\\ alpha _ {m} \ end {pmatrix}} - {\ begin {pmatrix} \ venstre \ langle y, \ varphi _ {1} \ høyre \ rangle \\\ venstre \ langle y, \ varphi _ {2} \ høyre \ rangle \\\ vdots \\\ venstre \ langle y, \ varphi _ {m } \ right \ rangle \\\ end {pmatrix}} = 0.}$

skrive ut, hvorved de vanlige skalar produktet symboliserer og kan også forstås som integralet av overlappingen av de grunnleggende funksjoner. De grunnleggende funksjonene skal leses som vektorer med de diskrete støttepunktene på stedet for observasjonene . ${\ displaystyle \ left \ langle \ cdot, \ cdot \ right \ rangle}$${\ displaystyle \ varphi _ {i}}$${\ displaystyle {\ vec {\ varphi _ {i}}} = (\ varphi _ {i} (x_ {1,1}, \ prikker, x_ {N, 1}), \ varphi _ {i} (x_ {1,2}, \ prikker, x_ {N, 2}), \ ldots, \ varphi _ {i} (x_ {1, n}, \ prikker, x_ {N, n}))}$${\ displaystyle n}$${\ displaystyle y = {\ vec {y}} = (y_ {1}, y_ {2}, \ ldots, y_ {n})}$

Videre kan minimeringsproblemet analyseres godt med en enestående nedbrytning . Dette motiverte også uttrykket av pseudo-inversen , en generalisering av det normale inverse av en matrise . Dette gir deretter et perspektiv på ikke-kvadratiske lineære ligningssystemer som tillater et ikke stokastisk, men algebraisk motivert løsningskonsept.

Numerisk behandling av løsningen

Det er to måter å løse problemet numerisk på. På den ene siden de normale ligningene

${\ displaystyle A ^ {T} A \ alpha = A ^ {T} y}$

som er unikt løselige hvis matrisen har full rang. Videre har produktsummen matrisen egenskapen til å være positiv bestemt , så dens egenverdier er alle positive. Sammen med symmetrien til , kan dette brukes til å løse problemet når man bruker numeriske metoder: for eksempel med Cholesky-spaltning eller CG-metoden . Siden begge metodene er sterkt påvirket av tilstanden til matrisen, er dette noen ganger ikke en anbefalt tilnærming: Hvis tilstanden allerede er dårlig, er kvadratet dårlig betinget. Som et resultat kan avrundingsfeil forsterkes i en slik grad at de gjør resultatet ubrukelig. Men regularisering kan metoder forbedre tilstanden. ${\ displaystyle A}$ ${\ displaystyle A ^ {T} A}$${\ displaystyle A ^ {T} A}$${\ displaystyle A}$${\ displaystyle A ^ {T} A}$

En metode er den såkalte ryggregresjonen , som går tilbake til Hoerl og Kennard (1970). Det engelske ordet ridge betyr noe som ridge, reef, back. I stedet for den dårlig betingede matrisen, brukes den bedre betingede matrisen her. Her er den dimensjonale identitetsmatrisen. Kunsten ligger i riktig valg av . For lite øker utholdenheten bare litt, for stor fører til en forvrengt tilpasning. ${\ displaystyle A ^ {T} A}$${\ displaystyle A ^ {T} A + \ delta I_ {m}}$${\ displaystyle I_ {m}}$${\ displaystyle m}$${\ displaystyle \ delta}$${\ displaystyle \ delta}$${\ displaystyle \ delta}$

På den annen side gir det opprinnelige minimeringsproblemet et mer stabilt alternativ, siden det med en liten verdi av minimumet har en tilstand i størrelsesorden av tilstanden til , med store kvadratverdier tilstanden til . En QR-spaltning brukes til å beregne løsningen , som genereres med husholdningstransformasjoner eller Givens-rotasjoner . Den grunnleggende ideen er at ortogonale transformasjoner ikke endrer den euklidiske normen til en vektor. Slik er det også ${\ displaystyle A}$${\ displaystyle A}$

${\ displaystyle \ | A \ alpha -y \ | _ {2} = \ | Q (A \ alpha -y) \ | _ {2}}$

for hver ortogonal matrise . For å løse problemet kan en QR-nedbrytning beregnes, hvor høyre side også transformeres direkte. Dette fører til et skjema ${\ displaystyle Q}$${\ displaystyle A}$

${\ displaystyle \ | R \ alpha -Q ^ {T} y \ | _ {2}}$

med hvor er en høyre øvre trekantmatrise . Løsningen på problemet oppnås således ved å løse ligningssystemet ${\ displaystyle R = {\ begin {pmatrix} {\ tilde {R}} \\ 0 \ end {pmatrix}},}$${\ displaystyle {\ tilde {R}} \ in \ mathbb {R} ^ {m \ times m}}$

${\ displaystyle {\ tilde {R}} {\ begin {pmatrix} \ alpha _ {1} \\\ vdots \\\ alpha _ {m} \ end {pmatrix}} = {\ begin {pmatrix} (Q ^ {T} y) _ {1} \\\ vdots \\ (Q ^ {T} y) _ {m} \ end {pmatrix}}.}$

Normets minimum oppstår da fra de gjenværende komponentene på den transformerte høyre siden, siden de tilknyttede ligningene aldri kan oppfylles på grunn av nulllinjene i . ${\ displaystyle (Qy) _ {m + 1}, \ dots, (Qy) _ {n},}$${\ displaystyle R}$

I statistisk regresjonsanalyse , gitt flere variabler, snakker man om flere lineære regresjoner . Den vanligste tilnærmingen, en multiple lineær modell for å estimere enn den vanlige minste kvadratestimasjonen eller vanlige minste kvadrater ( engelsk vanlig minste kvadrat , kort OLS ) kjent. I motsetning til den vanlige minste kvadratmetoden er generalisert minste kvadratmetoden , kort VMKQ ( engelsk generalisert minste kvadrat , kort tid GLS ) i en generalisert lineær regresjonsmodell som brukes. I denne modellen, de feilledd avvike fra fordelings antagelse slik som uncorrelatedness og / eller homoscedasticity . I motsetning til det, med multivariat regresjon, er det mange verdier for hver observasjon , slik at i stedet for en vektor er en matrise tilstede (se generell lineær modell ). De lineære regresjonsmodellene er forsket intenst i statistikk når det gjelder sannsynlighetsteori. Spesielt i økonometri analyseres for eksempel komplekse rekursivt definerte lineære strukturelle ligninger for å modellere økonomiske systemer. ${\ displaystyle x_ {1}, \ ldots, x_ {n}}$ ${\ displaystyle i}$ ${\ displaystyle (i = 1, \ prikker, n)}$ ${\ displaystyle r}$${\ displaystyle y}$${\ displaystyle n \ times r}$${\ displaystyle Y}$

Problemer med begrensninger

Ytterligere informasjon om parametrene er ofte kjent, som er formulert av sekundære forhold, som deretter er til stede i form av ligninger eller ulikheter. Likninger vises for eksempel når visse datapunkter skal interpoleres. Ulikheter vises oftere, vanligvis i form av intervaller for individuelle parametere. Fjærkonstanten ble nevnt i det innledende eksemplet; den er alltid større enn null og kan alltid estimeres oppover for den aktuelle saken.

Når det gjelder en ligning, kan disse brukes til et rimelig oppgitt problem for å transformere det opprinnelige minimeringsproblemet til en av en lavere dimensjon, hvis løsning automatisk oppfyller begrensningene.

Ulikhetssaken er vanskeligere. Problemet oppstår her med lineære ulikheter

${\ displaystyle \ min _ {\ alpha} \ | {\ vec {f}} - {\ vec {y}} \ | _ {2} \;}$med ,${\ displaystyle \; l \ leq C \ alpha \ leq u}$${\ displaystyle C \ in \ mathbb {R} ^ {n \ times n},}$

der ulikhetene er ment komponentmessig. Dette problemet kan løses unikt som et konveks og kvadratisk optimaliseringsproblem, og kan tilnærmes med metoder for å løse slike problemer , for eksempel.

Kvadratiske ulikheter oppstår for eksempel når man bruker en Tychonow-regulering for å løse integrerte ligninger . Løselighet er ikke alltid gitt her. Den numeriske løsningen kan for eksempel skje med spesielle QR-nedbrytninger .

Ikke-lineære modellfunksjoner

Grunnleggende idé og prosedyre

Spesielt ikke-lineær regresjon blir stadig viktigere med fremveksten av kraftige datamaskiner. Parametrene er inkludert i funksjonen på en ikke-lineær måte. Ikke-lineær modellering gjør i prinsippet at data kan tilpasses enhver formligning . Siden disse ligningene definerer kurver , brukes begrepene ikke-lineær regresjon og "kurvetilpasning" stort sett synonymt. ${\ displaystyle y = f (\ alpha)}$

Noen ikke-lineære problemer kan konverteres til lineære gjennom passende erstatning og deretter løses som ovenfor. En multiplikativ modell av skjemaet

${\ displaystyle y = \ alpha _ {0} \ cdot x ^ {\ alpha _ {1}}}$

kan konverteres til et additivsystem ved å ta for eksempel logaritmen . Denne tilnærmingen brukes blant annet i vekstteori .

Generelt oppstår et formproblem med ikke-lineære modellfunksjoner

${\ displaystyle \ min _ {\ alpha} \ | f (\ alpha) -y \ | _ {2},}$

med en ikke-lineær funksjon . Delvis differensiering resulterer da i et system med normale ligninger som ikke lenger kan løses analytisk. En numerisk løsning kan gjøres iterativt med Gauss-Newton-metoden . ${\ displaystyle f}$

Nåværende programmer fungerer ofte med en variant, Levenberg-Marquardt-algoritmen . Her er en regularisering den monotonien av den omtrentlige resultat garantert. I tillegg er metoden mer tolerant enn den opprinnelige metoden hvis det er større avvik i de estimerte verdiene. Begge metodene er relatert til Newtons metode, og under passende forhold (utgangspunktet er tilstrekkelig nær det lokale optimale), konvergerer de vanligvis kvadratisk , dvs. antallet riktige desimaler dobles i hvert trinn.

Hvis differensieringen er for tidkrevende på grunn av kompleksiteten til den objektive funksjonen, er en rekke andre metoder tilgjengelige som alternative løsninger som ikke krever noen avledninger, se metoder for lokal ikke-lineær optimalisering .

Eksempel fra enzymkinetikken til en ikke-lineariserbar modellfunksjon

Et eksempel på regresjonsmodeller som er helt ikke-lineære er enzymkinetikk . Kravet her er at "bare" (reaksjonshastighet) og ikke (substratkonsentrasjon) er gjenstand for en feil og kan dermed brukes som en variabel. Den Lineweaver-Burk-forholdet er en algebraisk riktig omdannelse av Michaelis-Menten-ligningen , men dens anvendelse bare gir riktige resultater dersom de målte verdiene er fri for feil. Dette oppstår fra det faktum at virkeligheten bare oppstår med et utvidet Michaelis-Menten-forhold ${\ displaystyle y}$${\ displaystyle \ alpha}$${\ displaystyle \ alpha}$ ${\ displaystyle v = V _ {\ mathrm {max}} \ cdot [S] / (K_ {m} + [S])}$

${\ displaystyle \ nu _ {i} = {\ frac {V _ {\ max} \ venstre [S_ {i} \ høyre]} {K_ {m} + \ venstre [S_ {i} \ høyre]}} ( 1 + e_ {i}) \ {\ boldsymbol {\ nu}} _ {i}}$

kan beskrives med som en feilparameter. Denne ligningen kan ikke lenger lineariseres, så løsningen må bestemmes iterativt her. ${\ displaystyle e_ {i}}$

Feil oppførsel hvis kravene ikke er oppfylt

Metoden med minste kvadrat gjør det mulig under visse forhold å beregne den mest sannsynlige av alle modellparametere. For å gjøre dette må en riktig modell ha blitt valgt, et tilstrekkelig antall måleverdier må være tilgjengelig og avvikene fra de målte verdiene fra modellsystemet må danne en normalfordeling . I praksis kan imidlertid metoden også brukes til forskjellige formål hvis disse kravene ikke blir oppfylt. Imidlertid bør det bemerkes at metoden med minste kvadrat kan gi helt uønskede resultater under visse ugunstige forhold. Det skal for eksempel ikke være noen avvik i de målte verdiene, da disse forvrenger estimeringsresultatet . I tillegg er multikollinearitet mellom parametrene som skal estimeres ugunstig fordi det gir numeriske problemer. Forøvrig kan regressorer som er langt fra de andre også ha sterk innflytelse på resultatene av justeringsberegningen. Man snakker her om verdier med stor innflytelse ( engelsk High Leverage Value ).

Multikollinearitet

Fenomenet multikollinearitet oppstår når målingene av to gitte variabler og veldig høy korrelasjon er så nesten lineære avhengige. I det lineære tilfellet betyr dette at determinanten til den normale ligningsmatrisen er veldig liten, og omvendt er normen for det inverse veldig stor; den tilstand av er derfor alvorlig svekket. De normale ligningene er da vanskelige å løse numerisk. Løsningsverdiene kan bli usannsynlig store, og til og med små endringer i observasjonene forårsaker store endringer i estimatene. ${\ displaystyle x_ {i}}$${\ displaystyle x_ {j}}$${\ displaystyle A ^ {T} A}$${\ displaystyle A ^ {T} A}$

Runaway

Dataverdier som “ikke passer inn i en serie målinger” er definert som avvikere . Disse verdiene har sterk innflytelse på beregningen av parametrene og forfalsker resultatet. For å unngå dette må dataene undersøkes for feil observasjoner. De oppdagede avvikene kan for eksempel elimineres fra måleserien, eller alternative beregningsmetoder som er avvikende motstandsdyktige, slik som vektet regresjon eller metoden med tre grupper, skal brukes.

I det første tilfellet, etter den første beregningen av de estimerte verdiene, brukes statistiske tester for å kontrollere om det er avvik i individuelle målte verdier. Disse målte verdiene blir deretter kastet og de estimerte verdiene blir beregnet på nytt. Denne metoden er egnet når det bare er noen få avvikere.

Ved vektet regresjon vektes de avhengige variablene avhengig av restene . Outliers, d. H. Observasjoner med store rester er gitt en lav vekt, som kan klassifiseres avhengig av restens størrelse. I algoritmen ifølge Mosteller og Tukey (1977), som kalles “biweighting”, vektes uproblematiske verdier med 1 og outliers med 0, noe som betyr at outlier blir undertrykt. I tilfelle vektet regresjon kreves det vanligvis flere iterasjonstrinn til settet med identifiserte avvikere ikke lenger endres. ${\ displaystyle y}$

Generelle modeller for minste kvadrater

Hvis de sterke kravene i prosedyren for feilbetingelsene blir myknet, oppnås såkalte generaliserte minste kvadrater . Viktige spesielle tilfeller har da egne navn, for eksempel de vektede minste kvadratene ( engelsk vektede minste kvadrater , kort tid WLS ) der feilene antas å være videre korrelert, men ikke mer av samme varians. Dette fører til et formproblem

${\ displaystyle \ | D (A \ alpha -y) \ | _ {2},}$

hvor D er en diagonal matrise . Hvis avvikene varierer sterkt, har de tilsvarende normale ligningene en veldig stor tilstand , og derfor bør problemet løses direkte.

Hvis man videre antar at feilene i måledataene også bør tas i betraktning i modellfunksjonen, resulterer "totalt minste kvadrat" i skjemaet

${\ displaystyle \ min _ {E, r} \ | (E, r) \ | _ {F}, (A + E) \ alpha = b + r,}$

hvor feilen er i modellen og feilen er i dataene.${\ displaystyle E}$${\ displaystyle r}$

Til slutt er det også muligheten for ikke å bruke en normalfordeling som grunnlag. Dette tilsvarer for eksempel minimeringen ikke i den euklidiske normen, men i sumnormen . Slike modeller er gjenstand for regresjonsanalyse .

litteratur

• Åke Björck: Numeriske metoder for problemer med minste kvadrater. SIAM, Philadelphia 1996, ISBN 0-89871-360-9 .
• Walter Großmann: Grunnleggende om utligningsberegningen. 3. utv. Utgave. Springer Verlag, Berlin / Heidelberg / New York 1969, ISBN 3-540-04495-7 .
• Richard J. Hanson, Charles L. Lawson: Løse problemer med minste kvadrat. SIAM, Philadelphia 1995, ISBN 0-89871-356-0 .
• Frederick Mosteller , John W. Tukey : Dataanalyse og regresjon - et andre kurs i statistikk. Addison-Wesley, Reading MA 1977, ISBN 0-201-04854-X .
• Gerhard Sacrifice: Numerisk matematikk for nybegynnere. En introduksjon for matematikere, ingeniører og informatikere. 4. utgave. Vieweg, Braunschweig 2002, ISBN 3-528-37265-6 .
• Peter Schönfeld: Methods of Econometrics. 2 bind. Vahlen, Berlin / Frankfurt 1969–1971.
• Eberhard Zeidler (red.): Lommebok for matematikk. Begrunnet v. I Bronstein, KA Semendjajew. Teubner, Stuttgart / Leipzig / Wiesbaden 2003, ISBN 3-8171-2005-2 .
• T. Strutz: Data Fitting and Usikkerhet (En praktisk introduksjon til vektede minste kvadrater og utover). 2. utgave. Springer Vieweg, 2016, ISBN 978-3-658-11455-8 .

weblenker

Individuelle bevis

1. ↑ Göttingen. I:  Goettingische annonser fra lærte ting / Goettingische annonser fra lærte ting / Goettingische lærte annonser , 23. januar 1802, s. 1 (online på ANNO ).Mal: ANNO / vedlikehold / gass
2. ^ Moritz Cantor :  Gauß: Karl Friedrich G. I: Allgemeine Deutsche Biographie (ADB). Volum 8, Duncker & Humblot, Leipzig 1878, s. 430-445., Her s. 436.
3. ↑ Paul Karlson: Magien av tall. Ullstein-Verlag, Berlin-Vest. Niende, revidert og utvidet utgave, 1967, s. 390 f.
4. ^ A. Abdulle, Gerhard Wanner : 200 år med minst firkantede metoder . I: Elements of Mathematics , bind 57, 2002, s. 45-60, doi: 10.1007 / PL00000559 .
5. F Jf. Moritz Cantor :  Gauß: Karl Friedrich G. I: Allgemeine Deutsche Biographie (ADB). Volum 8, Duncker & Humblot, Leipzig 1878, s. 430-445., S. 436.
6. ^ Adrien-Marie Legendre: Nouvelles méthodes pour la détermination des orbites des comètes. Paris 1805, s. 72–80 (vedlegg): Sur la Méthode des moindres quarrés.
7. ^ Carl Friedrich Gauß: Theoria Motus Corporum Coelestium in sectionibus conicis solem ambientium . Göttingen 1809; Carl Haase (oversettelse): Teori om bevegelsen til himmellegemene, som kretser rundt solen i kjeglesnitt. Hannover 1865.
8. ^ Matriser og determinanter .
9. ↑ Trykt i Gauss, Werke, bind X / 1, s. 380.
10. ↑ Abdulle, Wanner: Elements of Mathematics . Bind 57, 2002, s. 51. Med faks kopi av dagbokoppføringen.
11. ^ Laplace, sitert fra Herman Goldstine: En historie med numerisk analyse . Springer, 1977, s. 209.
12. ^ Carl Friedrich Gauß: Theoria kombinasjon er observasjon erroribus minimis obnoxiae. 2 deler. Göttingen 1821-1823 (Commentationes Societatis Regiae Scientiarum Gottingensis recentiores, classis mathematicae, bind 5.); Supplementum Theoria kombinasjon er observasjon erroribus minimis obnoxiae. Göttingen 1826/28 (Commentationes Societatis Regiae Scientiarum Gottingensis recentiores, classis mathematicae, bind 6.). Anton Börsch Paul Simon (red.): Avhandlinger om metoden med minste kvadrat av Carl Friedrich Gauss. På tysk språk. Berlin 1887, Textarchiv - Internet Archive .
13. ↑ Pete Stewart: Kanskje vi burde kalle det “Lagrangian Elimination” . NA Digest Søndag 21. juni 1991, 30. juni 1991 Volum 91, utgave 26.
14. ↑ H. Wirths: Relasjons Matematikk i Regresjon og korrelasjon . I: Stochastik in der Schule , 1991, utgave 1, s. 34–53
15. ↑ Hans R. Schwarz, Norbert Köckler: Numerisk matematikk. 7. revidert Utgave. Teubner, 2009, doi: 10.1007 / 978-3-8348-9282-9 , ISBN 978-3-8348-9282-9 , s. 141, kapittel 3.6 (Gaussisk tilnærming), setning 3.23.
16. ↑ AE Hoerl og RW Kennard: Ridge regression: Bias estimation for nonorthogonal problems , Techno Metrics 12 (1970), 55-82.
17. ^ Sabine Van Huffel, Joos Vandewalle: The Total Minst Squares Problem: Computational Aspects and Analysis. SIAM Publications, Philadelphia PA 1991, ISBN 0-89871-275-0 .
18. ↑ Martin Plesinger: Den totale Least Squares Problem og reduksjon av data i AX ≈ B. Dissertation. ( Memento fra 24. juli 2012 i Internet Archive ; PDF; 1,6 MB) TU Liberec og ICS Praha, 2008.

Denne versjonen ble lagt til i listen over artikler som er verdt å lese 27. august 2009 .