Endelig elementmetode

Den endelige elementmetode (FEM), også kjent som “ elementmetoden ”, er en generell numerisk metode brukes til forskjellige fysiske oppgaver . Den mest kjente er anvendelsen av FEM i styrke- og deformasjonsanalysen av faste stoffer med geometrisk komplekse former, fordi her viser det seg å være for tidkrevende eller ikke mulig å bruke klassiske metoder (f.eks. Stråleteorien ). Logisk sett er FEM basert på den numeriske løsningen av et komplekst system med differensialligninger .

Beregningsdomenet (f.eks. Som det faste stoffet) er lettere i et begrenset antall underregioner (z. B. delvis kropp) delt slik. B. i mange små kuboider eller tetraeder . De er de "endelige elementene". På grunn av deres enkle geometri kan deres fysiske oppførsel beregnes godt med kjente formfunksjoner . Hele kroppens fysiske oppførsel er simulert av hvordan disse elementene reagerer på kreftene, belastningene og grenseforholdene og hvordan belastninger og reaksjoner forplantes under overgangen fra ett element til det neste på grunn av svært spesifikke problemavhengige kontinuitetsforhold som tilnærmingen funksjoner må oppfylle.

Tilnærmingsfunksjonene inneholder parametere som vanligvis har en fysisk betydning, for eksempel B. forskyvning av et bestemt punkt i komponenten på et bestemt tidspunkt. Søket etter bevegelsesfunksjonen blir dermed redusert til søket etter verdiene til parametrene til funksjonene. Nøyaktigheten til den omtrentlige løsningen kan forbedres ved å bruke flere og flere parametere (f.eks. Flere og flere, mindre elementer) eller flere og mer verdifulle tilnærmingsfunksjoner.

Utviklingen av FEM var bare mulig i viktige stadier ved hjelp av utvikling av kraftige datamaskiner, da det krever betydelig datakraft. Derfor ble denne metoden formulert på en datavennlig måte fra begynnelsen. Det brakte et betydelig fremskritt i behandlingen av beregningsområder av hvilken som helst form.

introduksjon

Med FEM kan problemer fra forskjellige fysiske disipliner beregnes, siden det i utgangspunktet er en numerisk metode for å løse differensialligninger . For det første er beregningsområdet (“komponent”) delt inn i et stort antall elementer - tilstrekkelig fint. Disse elementene er endelig små, men deres faktiske størrelse forblir matematisk relevant - de er ikke "uendelig små" (uendelige). Inndelingen av området / komponenten i et visst antall elementer av endelig størrelse, som kan beskrives med et begrenset antall parametere, ga metoden navnet "finite element method".

Det er formfunksjoner for disse elementene (f.eks. Lokale Ritz-tilnærminger per element) som beskriver hvordan et element reagerer på ytre påvirkninger og grenseforhold. Hvis du setter inn disse formfunksjonene for alle elementene i differensiallikningene som skal løses, som beskriver de fysiske lovene, får du et stort sett veldig stort ligningssystem sammen med de innledende, grense- og overgangsbetingelsene. Å løse det (i det minste omtrent) er oppgaven til FE-ligningsløseren. Størrelsen på ligningssystemet som skal løses avhenger i stor grad av antall endelige elementer. Den omtrentlige løsningen representerer til slutt den numeriske løsningen til differensialligningen som blir vurdert. Hvis det er løst for alle elementer hvordan de oppfører seg under lastene, resulterer dette også i reaksjonen til hele komponenten.

Endelig, uendelig

Matematisk forblir størrelsen på hvert element relevant og må også tas med i beregningen, det er bare 'endelig' lite. Når det gjelder 'uendelig' små elementer, vil størrelsen være ubetydelig og ikke lenger bli tatt i betraktning i ligningene. I denne forbindelse forblir elementstørrelsen relevant.

En "tilstrekkelig fin" inndeling av komponenten i elementer er til stede hvis videre forbedring ikke lenger har noen vesentlig innflytelse på beregningsresultatet. DVS. det samlede resultatet er uavhengig av elementstørrelsen, som (fra dette synspunktet) da ikke lenger er relevant. Hvis elementstørrelsen fortsatt har en betydelig innvirkning på det samlede resultatet, så gjelder jeg. A. inngrepet som ikke fint nok.

historie

Bruken av FEM begynte i praksis på 1950-tallet med en strukturell beregning av flyvingene i luftfartsindustrien ( Turner , Clough 1956) og veldig snart også i kjøretøykonstruksjon. Metoden er basert på arbeidet ved Daimler AG i Stuttgart, som brukte det selvutviklede FEM-programmet ESEM (Elastostatic Element Method) lenge før datastøttet design (CAD) ble introdusert på begynnelsen av 1980-tallet. Begrepet finite element method ble først foreslått av RW Clough i 1960 og har blitt brukt overalt siden 1970-tallet. Den vanligste tyskspråklige betegnelsen for industrielle brukere er beregningsingeniør .

Historien om metoden med begrenset element fremgår av forskning og publikasjoner fra følgende forfattere (utvalg):

• Karl Heinrich Schellbach : Variasjonskalkulator ; Løsning av et minimalt arealproblem (1851/52)
• Ernst Gustav Kirsch: De grunnleggende ligningene til teorien om elastisiteten til faste legemer, avledet fra vurderingen av et poengsystem som er forbundet med elastiske stag (1868)
• John William Strutt, 3. baron Rayleigh (1842-1919): Om teorien om resonans. 1870
• Walter Ritz (1878–1909): ny metode for å løse variasjonsproblemer, Ritzs metode (1908/09)
• Boris G. Galerkin (1871–1945): Metode for vektede rester (1915)
• Erich Trefftz (1926): lokalt begrensede tilnærmingsfunksjoner; Motstykke til Ritz-metoden
• Hans Ebner (1929): Schubblech som et nivåelement i flykonstruksjon
• Alexander Hrennikoff (1896–1984): stangmodeller , utskifting av ruter med rammer, paneler med støtterist 1940/41
• Richard Courant (1888–1972): Variasjonsmetoder for løsning av problemer med likevekt og vibrasjon (er). 1943 (tilnærming fungerer med lokal støtte, elementvis tilnærminger for vibrasjonsproblemer)
• William Prager (1903–1980), John Lighton Synge (1897–1995): Tilnærming i elastisitet basert på begrepet funksjonsrom. 1947
• John Argyris (1913-2004): Kraft- og forskyvningsmetode for stangkonstruksjoner, matriksformulering (1954/55)
• MJ Turner, Ray W. Clough , HC Martin, LJ Topp: Stivhet og avbøyningsanalyse av komplekse strukturer. 1956 (første strukturelle beregning av flyvinger i Boeing , første anvendelse av FEM med dataprogram, første påføring av overflateelementer)
• Ray W. Clough (1920-2016): Den endelige elementmetoden i flyspenningsanalyse. 1960 (sannsynligvis første bruk av begrepet endelige elementer)
• Spierig (1963): Utvikling av trekantede elementer, overføring til skjell
• Olgierd Cecil Zienkiewicz (1921–2009), pioner for FEM og første standardverk (lærebok): The Finite Element Method in Structural and Continuum Mechanics , 1967 (med YK Cheung)
• Alfred Zimmer (* 1920) og Peter Groth (* 1938), pionerer for FEM, første tyske FEM-lærebok: Element Method of Elastostatics , 1969 Oldenbourg Verlag München, Wien
• Olga Alexandrovna Ladyschenskaja (1922–2004), Ivo Babuška (* 1926) og Franco Brezzi (* 1945) - Ladyschenskaja-Babuška-Brezzi betingelse for stabiliteten til et blandet endelig elementproblem med en sadelpunktstruktur
• Ivo Babuška (* 1926) - adaptive endelige elementalgoritmer

applikasjon

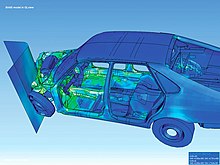
Den første anvendelsen av FEM var den lineære behandlingen av faste stoffer og strukturer i form av forskyvningsmetoden , og basert på denne mottok FEM impulser. Begrepet "endelige elementer" ble brukt litt senere. I den videre forskningen ble den endelige elementmetoden generalisert mer og mer og kan nå brukes i mange fysiske problemer, inkludert kan brukes i forskjellige sammenkoblede feltberegninger, værmeldinger eller til tekniske problemer innen bilindustrien, medisin, luftfart, mekanikk eller forbruksvarer innen industri. Et av hovedanvendelsesområdene for metoden er produktutvikling , der det blant annet beregnes mekaniske styrkeberegninger for enkeltkomponenter eller for eksempel komplette chassis- og karosserikonstruksjoner for å spare tidkrevende kollisjonstester .

Fremgangsmåte for en lineær mekanisk beregning (eksemplarisk)

Programmer som bruker finite element-metoden fungerer i henhold til EVA-prinsippet : Brukeren lager en (komponent) geometri i et CAD-program. Deretter foretar han ytterligere oppføringer i den såkalte FE-prosessoren . En FEM-ligningsløser utfører den faktiske beregningen, og brukeren mottar de beregnede resultatene, som han deretter kan se i den såkalte FE-postprosessoren i form av grafiske skjermer. Ofte kombineres forprosessoren og etterprosessoren i ett program eller er til og med en del av CAD-programmet.

Inngang: forprosessor

Den komponenten er utformet i den CAD program og overføres til FE preprosessoren ved hjelp av et direkte grensesnitt eller en nøytral utveksling format slik som STEP . Ved å velge nettverksparametere som elementstørrelse og elementtype (f.eks. Tetraeder, heksaheder i 3D) i nettmodulen, blir de endelige elementene generert ved hjelp av en nettingsalgoritme. For den mekaniske styrkeanalysen må materialets oppførsel angis, noe som i hovedsak indikerer hvilke reaksjoner komponenten har på ytre belastninger (f.eks. Deformasjon). Avhengig av materialet er forholdet mellom spenning og belastning forskjellig, og det er forskjellige deformasjoner. Hvis dette forholdet er lineært, kreves bare elastisitetsmodulen og Poissons forhold for FE-beregningen , ellers kreves ytterligere materialparametere og innganger i forprosessoren. Ytterligere grensebetingelser er for eksempel belastninger som virker på komponenten (krefter, trykk, temperatur, etc.). For å oppnå en representasjon som er så realistisk som mulig, er de homogene (begrensningene) og de inhomogene grenseforholdene (forskyvninger) samt alle belastninger som skal tas i betraktning på modellen spesifisert.

Behandling: ligningsløser

Avhengig av programmet brukes et separat (frittstående program) eller en integrert ligningsløser. Den beregner simuleringen av hvordan belastningene, kreftene og grenseforholdene påvirker de enkelte elementene i komponenten, og hvordan kreftene og effektene forplanter seg i komponenten og påvirker nærliggende elementer. Beregningen gir først en grov tilnærmet løsning. Ytterligere iterasjoner forbedrer tilnærmingen. De fleste iterasjoner beregnes til det bare er de minste endringene - da har tilnærmingen "konvergert" og er resultatet av simuleringen.

Utgang: postprosessor

Når det gjelder beregning av mekanisk styrke, mottar brukeren resultatet av FEM-ligningsløseren, spesielt verdier for spenning , deformasjon og forlengelse . Postprosessoren kan for eksempel vise dette i et falskt fargebilde . De ekvivalente spenningsverdiene brukes for eksempel for å verifisere styrken til en komponent.

Generell funksjonalitet

Diskretisering

Finite element-metoden er en diskret metode; H. løsningen beregnes på en diskret delmengde av basisarealet. For dette formålet er dette brutt ned i enkle delområder, de såkalte endelige elementene (nettverk, netting). Begrepet "endelig" understreker forskjellen til den analytiske betraktningen av uendelige dimensjoner. Hjørnene på de endelige elementene kalles noder. Disse nodene danner det diskrete delsettet for den numeriske metoden. Tilnærmingsfunksjoner introduseres på elementene, som inneholder de ukjente nodestørrelsene som parametere. De lokale tilnærmingene introduseres i den svake formuleringen av grenseverdiproblemet. De resulterende elementintegralene beregnes med numerisk kvadratur. Tilnærmingsmetodene er "integrert ut" slik at bare nodeverdiene forblir på elementene som ukjente etter integrasjonen. Elementligningene er satt sammen gjennom kontinuitetskrav ved elementgrensene. På denne måten blir grenseverdiproblemer for lineære partielle differensialligninger omgjort til et lineært ligningssystem med symmetriske systemmatriser. For ikke-lineære differensiallikninger kjører algoritmen analogt med forskjellen at de ikke-lineære avhengighetene er iterativt linearisert med egnede metoder (f.eks. Newtons metode), og det lineære ligningssystemet er satt opp for trinnvise størrelser i hvert deltrinn.

For visse oppgaver er underinndelingen i elementer i stor grad forhåndsbestemt av problemet, for eksempel i tilfelle romlige rammer der de enkelte stengene danner elementene i konstruksjonen. Dette gjelder også rammekonstruksjoner, der de enkelte bjelkene eller delte bjelkebitene representerer elementene i oppgaven. Ved todimensjonale problemer er grunnområdet delt inn i trekanter eller firkanter. Selv om det bare brukes rette elementer, kan en veldig god tilnærming av grunnområdet oppnås med en tilsvarende fin diskretisering . Krumlinjære elementer øker kvaliteten på tilnærmingen. I alle fall tillater denne diskretiseringen et fleksibelt opptak av basisområdet som også er tilpasset problemet. Det må imidlertid utvises forsiktighet for å unngå svært akutte eller stumpe vinkler ved elementets hjørneknuter for å utelukke numeriske vanskeligheter. Deretter erstattes det gitte området med arealet til de omtrentlige elementene. Den patch test kan senere brukes til å sjekke om det fungerte bra.

Romlige problemer løses med en inndeling av det tredimensjonale området i tetraedriske elementer , kuboidelementer eller andre elementer tilpasset problemet, muligens også med buede kanter, disse er jeg. d. R. Serendipity eller Lagrange-elementer , redigert.

Subtiliteten til underavdelingen, jeg. H. tettheten til nettverket har en avgjørende innflytelse på nøyaktigheten av resultatene av tilnærmingsberegningen. Siden databehandlingen øker når du bruker finere og tettere nettverk, er det viktig å utvikle nettverksløsninger som er så intelligente som mulig .

Elementtilnærming

I hvert av elementene velges en problemorientert tilnærming for funksjonen som søkes, eller mer generelt for funksjonene som beskriver problemet. Hele rasjonelle funksjoner i de uavhengige romlige koordinatene er spesielt egnet for dette. For endimensjonale elementer (medlemmer, bjelker) kommer polynomer av første, andre, tredje og noen ganger enda høyere grad i spørsmål. Ved todimensjonale problemer brukes lineære, kvadratiske eller høyere ordens polynomer. Type tilnærming avhenger av den ene siden av elementets form, og på den annen side kan problemet som skal behandles også påvirke tilnærmingen som skal velges. Fordi tilnærmingsfunksjonene må oppfylle veldig spesifikke problemavhengige kontinuitetsforhold ved overgangen fra ett element til det neste . Kontinuitetskravene er ofte åpenbare av fysiske årsaker og også nødvendige av matematiske årsaker. For eksempel må forskyvningen av et sammenhengende legeme i en retning være kontinuerlig når det går fra ett element til et annet for å sikre materialets kontinuitet. I tilfelle av en bjelke eller plate bøyning, er kontinuitetskravene høyere fordi det av analoge fysiske årsaker må kreves kontinuiteten til det første derivatet eller de to første delderivatene. Elementer med formfunksjoner som tilfredsstiller kontinuitetsbetingelsene kalles konforme.

For å faktisk oppfylle kontinuitetskravene, må funksjonskurven i elementet uttrykkes av funksjonsverdier og også av verdier av (partielle) derivater (nodpunktforskyvninger) i visse punkter i elementet, nodepunktene . Funksjonsverdiene og verdiene til derivater som brukes i nodene kalles elementvarenes nodevariabler. Ved hjelp av disse nodevariablene er tilnærmingsfunksjonen representert som en lineær kombinasjon av såkalte formfunksjoner med nodevariablene som koeffisienter.

Det anbefales å bruke et globalt koordinatsystem for nodekoordinatene i tillegg til en elementrelatert lokal. Begge er koblet sammen av transformasjonsfunksjoner. Hvis de samme formfunksjonene brukes til denne transformasjonen som for deformasjonsmetoden, er de isoparametriske elementer , for funksjoner av lavere eller høyere grad subparametriske eller superparametriske elementer.

grensebetingelser

Problem	Dirichlet-grensebetingelse / funksjonsverdi	Neumann grensetilstand
statisk problem	Støttetilstand / forskyvning	makt
Sivestrøm	Høyde på speilhøyde	Kilde eller vask
Ledning	temperatur	Varmestrøm eller varmeflyttetthet
elektrisk strøm	elektrisk spenning	Strømstyrke
Elektrostatikk	elektrisk spenning	elektrisk ladning
Magnetostatika	magnetisk potensial	magnetisk elv

Etter at et gitt problem er blitt diskretisert og elementmatrisene er satt opp, blir gitt randbetingelser introdusert . Et typisk FE-problem kan ha to typer grensebetingelser: Dirichlet-grensebetingelser og Neumann-grensebetingelser . De gjelder alltid (arbeid) ved nodene.

En Dirichlet-grensebetingelse spesifiserer direkte en funksjonsverdi og en Neumann-grensebetingelse spesifiserer et derivat av en funksjonsverdi. Hvis en Dirichlet-grensebetingelse er gitt, betyr dette at problemet blir en grad av frihet mindre og den tilhørende rad og kolonne i den totale matrisen blir slettet. Hvis Dirichlet-grensebetingelsen ikke er lik null, legges verdien til den lineære formen ("høyre side") i henhold til prefaktoren. Avhengig av typen fysisk problem, kan forskjellige fysiske størrelser være involvert, som vist som eksempel i tabellen. Neumann-grensevilkårene har også en andel i den lineære formen (“høyre side”).

En ytterligere variant er periodiske grensebetingelser , der verdiene ved den ene kanten tas som data for en annen kant, og dermed simuleres et periodisk uendelig kontinuerlig område. Såkalte sykliske grensebetingelser er definert for rotasjonssymmetriske problemer .

Grunnleggende ligninger av fortrengningsmetoden

Den forskyvning metode er den standardformulering av elementmetoden, hvor forskyvningene er de primære ukjente som beskriver translasjon, rotasjon og deformasjon av et fast stoff. Forskyvningsmetoden er tilgjengelig i alle vanlige programmer med begrenset element som problemer i solid mekanikk kan beregnes med. Det er flere grunnleggende ligninger for å løse solid state- problemer.

Prinsipp d'Alembert i Lagrangian-versjonen

En av ligningen som ligger til grunn for forskyvningsmetoden, som generelle problemer med solid mekanikk kan behandles med, er prinsippet til d'Alembert , som formulert i den Lagrangiske beskrivelsen av kontinuummekanikk . Med dette prinsippet kan både lineære problemer, for eksempel spørsmålet om naturlige vibrasjoner, og svært ikke-lineære problemer, som kollisjonstester , analyseres. Metoden for vektede rester i henhold til Galerkin, også kalt Galerkin-metoden eller Galerkin-tilnærming, brukes her.

Prinsipp om minimum potensiell energi

I konservative systemer , i tilfelle av et statisk problem, kan nodeforskyvninger bestemmes ut fra den tilstanden at den potensielle energien har et minimum i ønsket likevektstilstand . Med prinsippet om minimum potensiell energi kan stivhetsligningene til endelige elementer bestemmes direkte. Den potensielle energien til en struktur er summen av den interne belastningsenergien (den elastiske deformasjonsenergien) og potensialet til belastningene som påføres (arbeidet utført av eksterne krefter).

Bue-lengde metode

Buelengdemetoden er en metode der man kan beregne på en kraftstyrt måte opp til maksimal lastekapasitet. Nødvendigheten av kraftstyrte metoder er at man, i motsetning til forskyvningskontrollerte metoder, kan øke flere belastninger i direkte proporsjon. Med buelengdemetoden økes belastningen som spesifisert; Hvis denne økningen i belastning vil føre til for stor deformasjon, multipliseres belastningen med en faktor mindre enn 1, og til og med med negative verdier etter at lastekapasiteten er nådd.

Stokastisk endelig elementmetode

I varianten av den stokastiske endelige elementmetoden (SFEM) modelleres inngangsvariabler av modellen som er utsatt for en usikkerhet, for eksempel materialstyrker eller belastninger, ved hjelp av stokastiske variabler. Dette kan oppnås ved bruk av vanlige tilfeldige variabler . Tilfeldige felt brukes også ofte, som er tilfeldig varierende, kontinuerlige matematiske funksjoner. En vanlig beregningsmetode er Monte Carlo-simuleringen . FE-beregningen gjentas for mange tilfeldige implementeringer ( prøver ) av inngangsvariablene til en faller under en viss stokastisk feil definert på forhånd. Momentene, dvs. middelverdien og variansen, blir deretter beregnet fra alle resultatene. Avhengig av spredningen av inngangsvariablene er det ofte nødvendig med mange repetisjoner av FE-beregningen, noe som kan ta mye datatid.

Implisitte og eksplisitte FE-løsere

Strukturelle mekaniske FEM-systemer er representert av lineære ligningssystemer av 2. orden:

${\ displaystyle M {\ ddot {u}} (t) + D {\ dot {u}} (t) + Ku (t) = P (t)}$

${\ displaystyle M, D}$og er systemets masse-, dempnings- og stivhetsmatrise; er vektoren til de ytre kreftene som virker på modellen. er vektoren for gradene av frihet. ${\ displaystyle K}$${\ displaystyle P (t)}$${\ displaystyle u}$

Komplekse komponentmodeller består ofte av flere millioner noder, og hver node kan ha opptil 6 frihetsgrader. FEM-løsere (ligningssystemløsere) må derfor oppfylle visse krav med hensyn til effektiv minnestyring og, om nødvendig, bruk av flere CPUer. Det er to fundamentalt forskjellige typer FEM-løsere: implisitt og eksplisitt.

Implisitte FEM-løsere legger til grunn forutsetninger der den beregnede løsningsvektoren er gyldig. Apostlenes gjerninger z. B. en tidsmessig uforanderlig belastning på et system med demping, og etter en tilstrekkelig lang tid vil en konstant forskyvningsvektor bli etablert. For er da , og ligningssystemet forenkler til med løsningen${\ displaystyle u}$${\ displaystyle P (t) = P = konst.}$${\ displaystyle u (t) = u = konst.}$${\ displaystyle t \ to \ infty}$${\ displaystyle {\ ddot {u}} (t) = {\ dot {u}} (t) = 0}$${\ displaystyle Ku = P}$${\ displaystyle u = K ^ {- 1} P}$

For en gitt lastvektor kan forskyvningsvektoren beregnes ved hjelp av den Gaussiske algoritmen eller QR-dekomponering av . ${\ displaystyle P}$${\ displaystyle u}$${\ displaystyle K}$

Hvis et mekanisk system utsettes for harmonisk eksitasjon , kan det være nødvendig å bestemme systemets naturlige frekvenser for å unngå resonanser under drift. ${\ displaystyle P (t) = {\ hat {P}} \ sin (\ Omega t)}$

Naturlige frekvenser er alle frekvenser der en forskyvningsvektor representerer en løsning av det ulastede ( ) og ikke-dempede ( ) ligningssystemet. Følgende gjelder deretter hastighets- og akselerasjonsvektoren ${\ displaystyle \ omega _ {i}}$${\ displaystyle u (t) = {\ hat {u}} _ {i} \ sin (\ omega _ {i} t)}$${\ displaystyle P (t) = 0}$${\ displaystyle D = 0}$

${\ displaystyle {\ dot {u}} _ {i} = {\ hat {u}} _ {i} \ \ omega _ {i} \ cos (\ omega _ {i} t), \ {\ ddot { u}} _ {i} = - {\ hat {u}} _ {i} \ omega _ {i} ^ {2} \ sin (\ omega _ {i} t)}$

og ligningssystemet er altså

${\ displaystyle (-M \ omega _ {i} ^ {2} + K) {\ hat {u}} _ {i} \ sin (\ omega _ {i} t) = 0}$

For å beregne egenfrekvensene og de tilknyttede egenmodusene , må den implisitte løseren løse egenverdiproblemet ${\ displaystyle \ omega _ {i}}$${\ displaystyle {\ hat {u}} _ {i}}$

${\ displaystyle -M \ omega _ {i} ^ {2} + K = 0}$

å løse.

Eksplisitte FEM-løsere

Eksplisitte løsere beregner forskyvningsvektorene på bestemte diskrete tidspunkter innen et gitt tidsintervall. Knutepunktshastigheter og akselerasjoner er tilnærmet av differenskvotienter fra forskyvningene på suksessive tidspunkter . Med et konstant tidstrinn gjelder følgende ${\ displaystyle u_ {i}}$${\ displaystyle t_ {i}}$${\ displaystyle u_ {i + 1}, u_ {i}, u_ {i-1}}$${\ displaystyle t_ {i + 1}, t_ {i}, t_ {i-1}}$${\ displaystyle t_ {i + 1} -t_ {i} = \ Delta \ t}$

${\ displaystyle {\ dot {u}} = {\ frac {u_ {i} -u_ {i-1}} {\ Delta \ t}}}$

${\ displaystyle {\ ddot {u}} = {\ frac {{\ frac {u_ {i + 1} -u_ {i}} {\ Delta \ t}} - {\ frac {u_ {i} -u_ { i-1}} {\ Delta \ t}}} {\ Delta \ t}} = {\ frac {u_ {i + 1} -2u_ {i} + u_ {i-1}} {(\ Delta t) ^ {2}}}}$

det diskretiserte ligningssystemet har form

${\ displaystyle M {\ frac {u_ {i + 1} -2u_ {i} + u_ {i-1}} {(\ Delta t) ^ {2}}} + D {\ frac {u_ {i} - u_ {i-1}} {\ Delta \ t}} + Ku_ {i} = P_ {i}}$

Ved å løse denne ligningen oppnås et forhold som forskyvningsvektoren kan bestemmes ut fra vektorene som er beregnet tidligere og : ${\ displaystyle u_ {i + 1}}$${\ displaystyle u_ {i}}$${\ displaystyle u_ {i-1}}$

${\ displaystyle u_ {i + 1} = M ^ {- 1} ((\ Delta t) ^ {2} (P_ {i} -Ku_ {i}) - D \ Delta \ t (u_ {i} -u_ {i-1})) + 2u_ {i} -u_ {i-1}}$

Beregningen av det inverse utføres ikke i praksis, siden eksplisitte løsere vanligvis antar en diagonal matrise, og derfor må hver linje i ligningssystemet bare deles med diagonaloppføringen i den tilsvarende linjen . ${\ displaystyle M ^ {- 1}}$${\ displaystyle M}$${\ displaystyle M}$

Eksplisitte løsere brukes blant annet i kjøretøykonstruksjon for beregning av kollisjonsbelastningssaker.

Fordelen med direkte ligningsløsere i henhold til Gauss-metoden ligger i den praktiske anvendelsen i numerisk stabilitet og mottak av et eksakt resultat. Ulemper er dårlig kondisjonering av de vanligvis tynt befolkede stivhetsmatriser og de høye lagringskravene, som nevnt ovenfor. Iterative løsere er mindre følsomme for dårlig kondisjonering og krever mindre minne når elementlagring som ikke er null. Imidlertid bruker iterative løsere et avslutningskriterium for å beregne resultatene. Hvis dette oppnås før en omtrent nøyaktig løsning er funnet, kan resultatet, for eksempel en spenningskurve, lett tolkes feil.

I noen implementeringer er bare posisjonene og verdiene til oppføringene som avviker fra null lagret for de ofte forekommende sparsomme matrisene . Dette lar deg fortsette å løse ligningssystemene direkte, men sparer mye minne.

Isogeometrisk analyse

Noen programmer kan tilpasse et eksisterende FE-nett til en (veldig lik, ny) CAD-geometri, som vanligvis er vesentlig mindre enn den i tilfelle en (mindre) endring i (CAD) komponentgeometri Beregningstid som kreves.

Programmer

Endelig elementprogramvare og applikasjonen er nå en industri på flere milliarder dollar.

• I praksis er mange forskjellige store frittstående programmer med lignende bruksområder i bruk; valget av hvilket program du skal bruke, avhenger ikke bare av bruken, men også av faktorer som tilgjengelighet, sertifiseringsstandard i selskapet eller lisenskostnader.
• Med endelige elementpakker integrert i kommersielle CAD- systemer, kan enklere (vanligvis lineære) problemer beregnes og deretter vurderes direkte ved hjelp av CAD-systemet. De enkelte trinnene, f.eks. B. nettverksprosessen ( meshing ) kjøres automatisk i bakgrunnen.
• Siden det ofte kreves mye datakraft for å utføre beregningen, gjør de første selskapene datakraft tilgjengelig for brukerne i form av skytjenester.
• Det er forprosessorer / postprosessorer med et grafisk brukergrensesnitt og separate FE-løsere.
• Det er programrammer uten et grafisk brukergrensesnitt, mest som en forprosessor med en integrert ligningsløser, som drives av programmeringsspråk, for eksempel for å kontrollere FE-løseren med selvlagde tilleggsrutiner.

Matematisk avledning

Det undersøkte løsningsområdet deles først inn i delområder , de endelige elementene: ${\ displaystyle G}$${\ displaystyle G_ {1}, \ dotsc, G_ {m} \ subset G}$

${\ displaystyle G = \ bigcup _ {e = 1} ^ {m} G_ {e}}$.

Innvendig er den ønskede løsningsfunksjonen forskjellige formfunksjoner som nå er definert, som bare er noen få elementer som er lik henholdsvis null. Denne egenskapen er den virkelige årsaken til begrepet "endelige" elementer. ${\ displaystyle G}$${\ displaystyle f \ colon G \ to \ mathbb {R} ^ {k}}$${\ displaystyle \ psi _ {1}, \ dotsc, \ psi _ {n} \ colon G \ to \ mathbb {R} ^ {k}}$

Mulige løsninger for den numeriske tilnærmingen bestemmes av en lineær kombinasjon av formfunksjonene

${\ displaystyle f (x) = \ sum _ {i = 1} ^ {n} c_ {i} \ cdot \ psi _ {i} (x) \ quad, c_ {i} \ in \ mathbb {R}}$.

Siden hver testfunksjon forsvinner på de fleste elementene, kan funksjonen som er begrenset til elementet, omvendt beskrives av den lineære kombinasjonen av færre testfunksjoner . ${\ displaystyle G_ {e}}$${\ displaystyle f | G_ {e}}$${\ displaystyle \ psi _ {i}}$

Hvis differensiallikningene og grensebetingelsene til problemet kan representeres som lineære operatorer med hensyn til funksjonene , fører dette til et lineært ligningssystem med hensyn til de frie variablene til den lineære kombinasjonen : ${\ displaystyle f}$${\ displaystyle c_ {i}}$

${\ displaystyle D (c) = g}$

Med

${\ displaystyle D}$= Lineær kartlegging av til et funksjonelt rom${\ displaystyle \ mathbb {R} ^ {n}}$

${\ displaystyle c}$ = Vektor av lineære kombinasjonsfaktorer ${\ displaystyle c_ {i}}$

${\ displaystyle g}$ = Funksjon som representerer differensiallikningen og grensebetingelsene

For å oppnå et endelig lineært ligningssystem, modelleres også verdiområdet ved bruk av tilnærmingsfunksjoner . Deretter kan det beskrives ved hjelp av lineære kombinasjoner : ${\ displaystyle D}$${\ displaystyle \ phi _ {1}, \ dotsc, \ phi _ {n}}$${\ displaystyle g}$${\ displaystyle \ phi _ {i}}$

${\ displaystyle g (x) = \ sum _ {i = 1} ^ {n} b_ {i} \ cdot \ phi _ {i} (x) \ quad, b_ {i} \ in \ mathbb {R}}$

og ligningssystemet oppnås samlet

${\ displaystyle A \ cdot c = b}$

Med

${\ displaystyle A}$ = kvadratmatrise med ${\ displaystyle A = \ phi ^ {- 1} \ cdot D}$

${\ displaystyle c}$ = Vektor av lineære kombinasjonsfaktorer ${\ displaystyle c_ {i}}$

${\ displaystyle b}$ = Vektor av lineære kombinasjonsfaktorer ${\ displaystyle b_ {i}}$

Dimensjonen til matrisen er resultatet av antall tilnærmingsfunksjoner multiplisert med frihetsgraden som den fysiske modellen er basert på . Dimensjonen til matrisen er antall totale frihetsgrader, der spesifikasjoner som tilsvarer modellen med hensyn til det unike ved problemet (f.eks. De stive kroppsforskyvningene i tilfelle en elastisk kropp) må utelukkes. ${\ displaystyle k}$

Fordi hvert element bare er koblet til noen få nærliggende elementer, er de fleste verdiene til den totale matrisen null, slik at den er "tynt befolket". I de fleste brukstilfeller brukes de samme funksjonene som batchfunksjoner og testfunksjoner . I dette tilfellet er matrisen også symmetrisk rundt hoveddiagonalen . ${\ displaystyle \ psi _ {i}}$${\ displaystyle \ phi _ {i}}$

Hvis antall frihetsgrader ikke er for stort (opptil ca. 500 000), kan dette ligningssystemet løses mest effektivt ved å bruke en direkte metode , for eksempel med den Gaussiske eliminasjonsmetoden . Den sparsomme strukturen i ligningssystemet kan brukes effektivt her. Mens beregningsinnsatsen for ligninger er med Gauss-algoritmen , kan innsatsen reduseres betydelig ved smart pivotvalg (f.eks. Markowitz-algoritme eller grafteoretiske tilnærminger ). ${\ displaystyle N}$${\ displaystyle {\ mathcal {O}} (N ^ {3})}$

For mer enn 500.000 ukjente gjør den dårlige tilstanden til ligningssystemet direkteløsere stadig vanskeligere, slik at iterative løsere som forbedrer en løsning trinn for trinn, vanligvis brukes til store problemer . Enkle eksempler på dette er Jacobi- og Gauss-Seidel-metodene , men i praksis brukes multigridmetoder eller forhåndskonditionerte Krylow-underrommetoder , slik som konjugatgradienten eller GMRES- metoden . På grunn av størrelsen på ligningssystemene er det noen ganger nødvendig å bruke parallelle datamaskiner.

Hvis den delvise differensiallikningen er ikke-lineær , er det resulterende ligningssystemet også ikke-lineært. Dette kan vanligvis bare løses ved hjelp av numeriske tilnærmingsmetoder. Et eksempel på en slik metode er Newton-metoden der et lineært system løses trinn for trinn.

Det er nå et stort antall kommersielle dataprogrammer som bruker finite element-metoden.

Svak formulering

En elliptisk delvis differensialligning kan formuleres svakt, dvs. H. problemet kan uttrykkes på en måte som krever mindre jevnhet i løsningen . Den gjør dette som følger.

Gitt et Hilbert-rom , en funksjonell (funksjon fra sitt dobbelte rom) , samt en kontinuerlig og elliptisk bilinær form , kalles løsningen på variasjonsproblemet hvis ${\ displaystyle H}$${\ displaystyle f \ in H ': = \ {g: \; H \ rightarrow \ mathbb {R} | \; g {\ text {er lineær og kontinuerlig}} \}}$${\ displaystyle H}$ ${\ displaystyle a (\ cdot, \ cdot)}$${\ displaystyle u \ i H}$

${\ displaystyle a (u, v) = f (v) \ \ forall v \ i H}$.

Eksistensen og unikheten til løsningen gir representasjonssetningen Fréchet Riesz (for tilfelle at den bilineære formen er symmetrisk) eller lemmaet Lax-Milgram (generelt tilfelle). ${\ displaystyle u}$${\ displaystyle a}$

Vi vet at rommet er et Hilbert-rom . Basert på dette kan Sobolew-rommene defineres ved hjelp av det såkalte svake derivatet . ${\ displaystyle L ^ {2} (\ Omega): = \ {f: \ Omega \ rightarrow \ mathbb {R} \ | \ \ | f \ | _ {L ^ {2}} <\ infty \}}$ ${\ displaystyle H ^ {s} (\ Omega)}$

Problemet kan sees på som en variant av en delvis differensialligning i ett område . ${\ displaystyle a (u, v) = f (v)}$${\ displaystyle \ Omega}$

Poisson-problemet som et eksempel:

${\ displaystyle - \ Delta u (x) = f (x) \ \ forall x \ i \ Omega}$

${\ displaystyle u (x) = 0 \ \ forall x \ in \ partial \ Omega}$

der her betegner den Laplace-operator . En multiplikasjon med uendelig ofte kontinuerlig differensierbare funksjoner resulterer etter en integrering ${\ displaystyle \ Delta}$${\ displaystyle \ psi \ in C_ {0} ^ {\ infty} (\ Omega)}$

${\ displaystyle \ Leftrightarrow - \ int _ {\ Omega} \ Delta u \, \ psi \, dx = \ int _ {\ Omega} f \, \ psi \, dx \ \ forall \ psi \ in C_ {0} ^ {\ infty} (\ Omega).}$

En delvis integrasjon (First Greens formel ) og nullgrensevilkårene for deretter å levere ${\ displaystyle \ psi}$

${\ displaystyle \ Leftrightarrow \ int _ {\ Omega} \ nabla u \, \ nabla \ psi \, dx = \ int _ {\ Omega} f \, \ psi \, dx \ \ forall \ psi \ in C_ {0 } ^ {\ infty} (\ Omega)}$

Nå er en elliptisk og kontinuerlig bilinær form på , og høyre side er en kontinuerlig lineær form${\ displaystyle a (u, \ psi): = \ int _ {\ Omega} \ nabla u \, \ nabla \ psi \, dx}$${\ displaystyle H_ {0} ^ {1} (\ Omega): = {\ overline {C_ {0} ^ {\ infty} (\ Omega)}} ^ {\ | \ cdot \ | _ {H ^ {1 }}}}$${\ displaystyle (f, \ psi) _ {L ^ {2}} = f (\ psi)}$${\ displaystyle H_ {0} ^ {1} (\ Omega)}$

Hvis funksjonsrommet / Hilbert-rommet under vurdering har et begrenset grunnlag, kan et lineært ligningssystem oppnås fra variasjonsformuleringen.

For funksjonsrom bestemmer valg av grunnlag effektiviteten i prosessen. Bruk av splines med trianguleringer og, i visse tilfeller, den diskrete Fourier-transformasjonen (splitting i sinus og cosinus) er vanlig her.

På grunn av fleksibilitetshensyn når det gjelder områdets geometri , blir følgende tilnærming vanligvis valgt. ${\ displaystyle \ Omega}$

Området diskretiseres ved å dele det i trekanter og bruke splines assosiert med toppunktene p for å spenne det endelige dimensjonale funksjonsrommet . Splines møtes på bestemte punkter i trekanter (hvor δ er Kronecker-deltaet ). Så du kan da representere en diskret funksjon gjennom ${\ displaystyle \ Omega}$${\ displaystyle \ lambda _ {p} (x)}$${\ displaystyle \ Omega}$${\ displaystyle \ lambda _ {p} (q) = \ delta _ {pq}}$${\ displaystyle u_ {h} (x)}$

${\ displaystyle u_ {h} (x) = \ sum _ {p} u_ {p} \, \ lambda _ {p} (x)}$

med koeffisientene knyttet til den grunnleggende representasjonen. På grunn av det endelige grunnlaget trenger du ikke lenger å teste mot alle , men bare mot alle basisfunksjoner; formuleringen av variasjoner er redusert til på grunn av lineariteten ${\ displaystyle u_ {p}}$${\ displaystyle \ psi \ i H_ {0} ^ {1}}$

${\ displaystyle a (u_ {h}, \ lambda _ {q}) = \ sum _ {p} u_ {p} \, a (\ lambda _ {p}, \ lambda _ {q}) = (f, \ lambda _ {q}) \ \ forall q}$

Så vi har et system med lineære ligninger å løse

${\ displaystyle A \ cdot u = f}$,

Med

${\ displaystyle A_ {pq} = a (\ lambda _ {p}, \ lambda _ {q})}$

og

${\ displaystyle f_ {q} = (f, \ lambda _ {q})}$

Dette resultatet oppnås med alle endelige grunnlag i Hilbert-rommet.

eksempel

Formell definisjon av det endelige elementet (ifølge Ciarlet )

Et endelig element er en trippel , der: ${\ displaystyle E = (T, \ Pi, \ Sigma)}$

• ${\ displaystyle T}$ er et ikke-tomt område (f.eks. trekanter, firkanter, tetraeder, etc.)
• ${\ displaystyle \ Pi}$er et endelig-dimensjonalt rom med formfunksjoner (lineære, kvadratiske eller kubiske formfunksjoner, dvs. splines, sines, etc.) formfunksjoner${\ displaystyle \ rightarrow}$
• ${\ displaystyle \ Sigma}$er et sett med lineært uavhengige funksjoner på nodevariabler${\ displaystyle \ Pi}$ ${\ displaystyle \ rightarrow}$

Det gjelder funksjonalitetene at de er knyttet til basens funksjoner:

${\ displaystyle \ sigma _ {i} \ in \ Sigma: \ sigma _ {i} (\ pi _ {j}) = \ delta _ {ij} \ \ j \ in \ {1, \ ldots, \ dim ( \ Pi) \}}$

Det gjelder alle funksjoner

${\ displaystyle v \ in \ Pi: v (x) = \ sum _ {i} \ sigma _ {i} (x) \, \ pi _ {j}}$.

For sinus som grunnfunksjon er im da ${\ displaystyle \ mathbb {(} R) ^ {1}}$

${\ displaystyle \ operatorname {span} \, \ left \ {\ sin (x), \ sin (2x), \ ldots, \ sin (nx) \ right \} = \ Pi}$

og det funksjonelle

${\ displaystyle \ sigma _ {i} (\ psi): = (\ sin (ix), \ psi) _ {L ^ {2}}}$.

For splines, derimot, er det punktet evaluering på de spesifiserte punktene av trekantene nok: . ${\ displaystyle \ sigma _ {p} (\ psi): = \ psi (p)}$

S1: Lineære elementer på trekanter

Den FEM plass av kontinuerlige, stykkevis lineære funksjoner er definert som:

${\ displaystyle S ^ {1} (\ Omega, T): = \ left \ lbrace u \ in C ^ {0} (\ Omega) \; | \; {u |} _ {\ Delta} (x, y ) = a _ {\ Delta} + b _ {\ Delta} x + c _ {\ Delta} y \ quad \ forall \ Delta \ in T \ right \ rbrace}$,

hvor er en region og trianguleringen av regionen med trekanter og betegner begrensningen av den kontinuerlige funksjonen til trekanten . ${\ displaystyle \ Omega \ subset \ mathbb {R} ^ {2}}$${\ displaystyle T \ subset \ Omega}$${\ displaystyle \ Delta}$${\ displaystyle {u |} _ {\ Delta}}$${\ displaystyle u}$${\ displaystyle \ Delta \ i T}$

P1: Lineært referanseelement på en trekant

Referanseelementet er definert som: ${\ displaystyle {\ hat {T}}}$

${\ displaystyle {\ hat {T}} = \ left \ lbrace (x, y) \ in \ mathbb {R} ^ {2} | 0 <x <1 \; {\ text {and}} \; 0 < y <1-x \ right \ rbrace.}$

De lineære elementene er funksjoner av typen: ${\ displaystyle P1}$

${\ displaystyle p \ colon {\ hat {T}} \ to \ mathbb {R}, (x, y) \ mapsto a + bx + cy \ quad {\ text {with}} \; a, b, c \ i \ mathbb {R}.}$

For å definere funksjonen er det tilstrekkelig å spesifisere verdiene i hjørnepunktene . Derfor kan alle funksjoner vises med grunnleggende funksjoner : ${\ displaystyle p}$${\ displaystyle {\ har {E_ {1}}}: = (0,0), {\ har {E_ {2}}}: = (1,0), {\ har {E_ {3}}}: = (0,1)}$${\ displaystyle p}$${\ displaystyle {\ hat {\ phi}} _ {i}}$

${\ displaystyle p (x, y) = \ sum _ {i = 1} ^ {3} \ alpha _ {i} {\ hat {\ phi}} _ {i} (x, y) \ quad {\ text {med}} \; \ alpha _ {i} \ i \ mathbb {R}.}$

De grunnleggende funksjonene er gitt som lineære funksjoner som bare er null på ett hjørnepunkt:

${\ displaystyle {\ hat {\ phi}} _ {i} ({\ hat {E_ {j}}}) = \ delta _ {i, j} \ quad \ forall i, j = 1,2,3}$

der er en kronecker-delta -funksjonen. ${\ displaystyle \ delta}$

Transformasjon av referanseelementet

For å koble referanseelementet til en vilkårlig trekant (vertices:) bruker man en lineær transformasjon : ${\ displaystyle T}$${\ displaystyle E_ {1}, E_ {2}, E_ {3}}$ ${\ displaystyle F_ {T}}$

${\ displaystyle {\ begin {align} F_ {T} & \ kolon {\ hat {T}} \ til T, \ quad F (v) = B_ {T} v + b_ {T} \\ B_ {T} &: = \ venstre (E_ {2} -E_ {1}, E_ {3} -E_ {1} \ høyre), \ quad b_ {T}: = E_ {1}. \ slutt {justert}}}$

I mange problemer knyttet til partielle differensiallikninger , må skalarproduktet til basisfunksjoner (definert i en hvilken som helst trekant ) beregnes: ${\ displaystyle L ^ {2}}$${\ displaystyle \ phi _ {i}}$${\ displaystyle T}$

${\ displaystyle (\ nabla \ phi _ {i}, \ nabla \ phi _ {j}) _ {L ^ {2} (T)} = \ int _ {T} \ nabla \ phi _ {i} (x ) \ cdot \ nabla \ phi _ {j} (x) dx.}$

Ved hjelp av transformasjonssettet kan integrasjonen flyttes til referanseelementet:

${\ displaystyle \ int _ {T} \ nabla \ phi _ {i} (x) \ cdot \ nabla \ phi _ {j} (x) dx = \ int _ {\ hat {T}} \ left (\ left (DF_ {T} (z) \ right) ^ {- T} \ nabla {\ hat {\ phi}} _ {i} (z), \ left (DF_ {T} (z) \ right) ^ {- T} \ nabla {\ hat {\ phi}} _ {j} (z) \ right) _ {\ mathbb {R} ^ {2}} | \ det DF_ {T} (z) | dz.}$

litteratur

• Martin Mayr / Ulrich Thalhofer: Numeriske løsningsmetoder i praksis: FEM-BEM-FDM . Hanser, 1993, ISBN 3-446-17061-8 , pp. 312 . 
• JN Reddy: Energiprinsipper og variasjonsmetoder i anvendt mekanikk . 2. utgave. John Wiley & Sons, 2002, ISBN 0-471-17985-X . 
• D. Braess: Finite Element Theory, Fast Solvers and Applications in Elasticity Theory . 4. utgave. Springer, 2007, ISBN 978-3-540-72449-0 . 
• Günter Müller (red.): FEM for utøvere . 4 bind. Ekspert Verlag, Renningen. 
  • Volum 1: Grunnleggende: Grunnleggende kunnskaper og arbeidseksempler for FEM-applikasjoner. 2007, ISBN 978-3-8169-2685-6 .
  • Volum 2: Strukturell dynamikk. 2008, ISBN 978-3-8169-2842-3 .
  • Volum 3: Temperaturfelt. 2007, ISBN 978-3-8169-2714-3 .
  • Volum 4: Elektroteknikk. 2009, ISBN 978-3-8169-2841-6 .
• Klaus-Jürgen Bathe: Endelige elementmetoder . 2. utgave. Springer-Verlag, 2002, ISBN 3-540-66806-3 . 
• VI Gawehn: Finite Element Method . BOD Book on Demand, 2009, ISBN 978-3-8370-2497-5 (FEM grunnleggende for statikk og dynamikk). 
• Frank Rieg, Reinhard Hackenschmidt, Bettina Alber-Laukant: Endelig elementanalyse for ingeniører: En lett å forstå introduksjon . Hanser Fachbuchverlag, 2012, ISBN 978-3-446-42776-1 (anvendelse av FEM i ingeniørfag). 
• René de Borst , Mike Crisfield , Joris Remmers, Clemens Verhoosel: Ikke-lineær endelig elementanalyse av faste stoffer og strukturer , Wiley-VCH 2014
• Karl-Eugen Kurrer : Historien om teorien om strukturer. Søker etter likevekt , Ernst og Son 2018, s. 881–914, ISBN 978-3-433-03229-9

weblenker

• Finite element-metoden innen biomedisin, biomekanikk og relaterte områder.
• Numeriske metoder (forelesning og praksis, manus) ( Memento fra 20. oktober 2018 i Internet Archive )
• FU Mathiak: Finite element method (FEM). ( Minne 26. november 2019 i Internet Archive ) [PDF; 3,86 MB].

Individuelle bevis

1. ^ Karl Schellbach: Problemer med beregningen av variasjoner . I: Tidsskrift for ren og anvendt matematikk . teip 41 , nei 4 , 1852, s. 293-363 . 
2. ↑ Ernst Gustav Kirsch: De grunnleggende ligningene til teorien om elastisitet av faste legemer, avledet fra vurderingen av et poengsystem som er forbundet med elastiske stag. I: Journal of the Association of German Engineers , bind 7 (1868), utgave 8.
3. ^ John William Strutt: Om teorien om resonans . I: Philosophical Transactions of the Royal Society of London . teip 161 , 1871, s. 77-118 . 
4. ↑ Walter Ritz: Om en ny metode for å løse visse variasjonsproblemer i matematisk fysikk . I: Tidsskrift for ren og anvendt matematikk . teip 135 , 1909, s. 1-61 . 
5. ↑ Christoph Haderer: Extension and Parameter Studies of a 1-D Stochastic Finite Element Code with Random Fields. Engineering Risk Analysis Group. Teknisk universitet i München, 2017.
6. ^ David Roylance: Endelig elementanalyse . (PDF; 348 kB), åpnet 10. mai 2017.