Vektorpakke

Grafikken over viser sirkelen med noen av dens tangensrom . Den andre grafikken oppsummerer tangentområdene for den tangentielle bunten , en spesiell vektorpakke.

Vektorbunter eller noen ganger også vektorromsbunter er familier av vektorrom som parametriseres av punktene i et topologisk rom . Vektorbunter tilhører derfor også fiberbunter . Hvis det er et sett med baser for hvert vektorrom i vektorpakken , kan dette settet også danne en fiberbunt. Man snakker da om rammebunter eller også om bunter. Disse spesielle fiberbunter er også hovedfiberbunter .

En vektorpakke består tydelig av ett vektorrom for hvert punkt i basisrommet. Men siden vektorrom med samme dimensjon alltid er isomorfe, ligger den essensielle informasjonen i forholdet mellom disse vektorområdene. Det mest kjente eksemplet på en vektorpakke er den tangentielle bunten til et differensierbart manifold . Forholdet mellom de forskjellige tangensielle rommene, dvs. vektorrommene for de enkelte punktene, kommer for eksempel til uttrykk i spørsmålet om et vektorfelt er differensierbart.

Spørsmålet om hvordan vektorbunter kan se ut i et rom er nært knyttet til globale topologiske egenskaper i rommet. Ikke-isomorfe vektorbunter kan ofte kjennetegnes ved deres karakteristiske klasser .

Definisjoner

Vektorpakke

Illustrasjon av vektorpakken . Her er total plass og basisplass . Figuren projiserer hver rette linje på punktet . Plassen kalles fiber over . I tillegg er total plass foreningen av alle fibre.${\ displaystyle (E, B, \ pi)}$${\ displaystyle E = \ mathbb {R} ^ {2}}$${\ displaystyle B = \ mathbb {R}}$${\ displaystyle \ pi \ colon E \ to B}$${\ displaystyle E_ {x}}$${\ displaystyle x}$${\ displaystyle E_ {x} = \ {p \ in E | \ pi (p) = x \}}$${\ displaystyle x}$${\ displaystyle E}$

La være et reelt eller et komplekst n-dimensjonalt vektorrom. En ekte eller kompleks vektorbunt av rang er en trippel , bestående av topologiske mellomrom (total plass) og (base) , samt en kontinuerlig kartlegging av surjektiv , slik at: ${\ displaystyle \ mathbb {K} ^ {n}}$${\ displaystyle n}$${\ displaystyle (E, B, \ pi)}$ ${\ displaystyle E}$ ${\ displaystyle B}$ ${\ displaystyle \ pi \ colon E \ to B}$

• For hvert punkt av fiberen bidrar fra omtrent strukturen til et reelt eller komplekst n- dimensjonalt vektorrom .${\ displaystyle x}$${\ displaystyle B}$${\ displaystyle E_ {x}: = \ pi ^ {- 1} (x)}$${\ displaystyle E}$${\ displaystyle x}$
• “Lokal triviality”: For hvert punkt er det et miljø av og homeomorfi${\ displaystyle x \ i B}$ ${\ displaystyle U}$${\ displaystyle x}$

${\ displaystyle \ psi \ colon U \ times \ mathbb {K} ^ {n} \ to E | _ {U}: = \ pi ^ {- 1} (U) \ subseteq E}$,

hvem er kompatibel med , det vil si og for ${\ displaystyle \ pi}$${\ displaystyle \ pi \ circ \ psi = \ operatorname {pr} _ {1}}$

${\ displaystyle \ psi _ {y} \ colon \ {y \} \ times \ mathbb {K} ^ {n} \ to E_ {y}}$

for hver i en er isomorfisme av vektorrom. Den fremspring på den første faktoren betegner . Slikt kalles lokal trivialisering .${\ displaystyle y}$${\ displaystyle U}$${\ displaystyle \ operatorname {pr} _ {1}}$${\ displaystyle \ psi}$

En vektorpakke kalles trivial hvis det er en trivialisering med . er en triviell bunt med vektorer. ${\ displaystyle (E, B, \ pi)}$${\ displaystyle U = B}$${\ displaystyle (B \ times \ mathbb {K} ^ {n}, B, \ operatorname {pr} _ {1})}$

I forkortet form snakker man ofte om ”vektorpakken ”, som implisitt betegner trippelen . ${\ displaystyle \ pi \ colon E \ to B}$${\ displaystyle (E, B, \ pi)}$

Linjebunt

En vektorpakke med rangering 1 kalles en rettlinjebunt (også kalt en linjebunt som en feiloversettelse fra engelsk ).

Eksempler

Möbius-stripen som en vektorpakke over sirkelen

• Den tangent bunt av en differensierbar manifold er en vektor bunt bestående av de tangent områder av manifolden. Tilsvarende er den cotangensielle bunten som består av de cotangensielle rommene - det vil si de doble rommene i de tangensielle rommene - en vektorpakke.
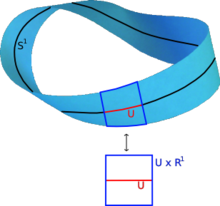
• Den Möbius strimmel er en bunt av rette linjer over 1-sfære ( sirkel ) . Lokalt er det homomorf til , hvor er en åpen delmengde av . Imidlertid er Möbius-stripen ikke homomorf til hva en sylinder ville være.${\ displaystyle S ^ {1}}$${\ displaystyle U \ times \ mathbb {R}}$${\ displaystyle U}$${\ displaystyle S ^ {1}}$${\ displaystyle S ^ {1} \ times \ mathbb {R}}$
• Som en pakke med ekstern algebra er rommet til differensialformer også en vektorpakke.
• Den - tensor bunt er også en vektor pakke som inkluderer de som er nevnt tidligere vektorbunter som spesialtilfeller.${\ displaystyle (r, s)}$

Homomorfisme av vektorbunter

Homomorfisme

En vektor bunt homomorfi fra vektoren bunten til vektoren bunten er et par av kontinuerlige kart og , slik det ${\ displaystyle \ pi _ {1} \ colon E_ {1} \ to B_ {1}}$${\ displaystyle \ pi _ {2} \ colon E_ {2} \ to B_ {2}}$${\ displaystyle (f, g)}$ ${\ displaystyle f \ colon E_ {1} \ to E_ {2}}$${\ displaystyle g \ colon B_ {1} \ to B_ {2}}$

• ${\ displaystyle g \ circ \ pi _ {1} = \ pi _ {2} \ circ f}$ gjelder og
• ${\ displaystyle \ pi _ {1} ^ {- 1} (\ {x \}) \ til \ pi _ {2} ^ {- 1} (\ {g (x) \})}$er et lineært kart for alle .${\ displaystyle x \ i B_ {1}}$

En vektorbunt homomorfisme blir ofte referert til som en bunt homomorfisme eller en homomorfisme for kort.

Isomorfisme

En vektorpakke-homomorfisme fra til er en vektorpakke- isomorfisme hvis og er homeomorfismer, og den induserte lineære kartleggingen er en vektorrom-isomorfisme . ${\ displaystyle (f, g)}$${\ displaystyle \ pi _ {1} \ colon E_ {1} \ to B_ {1}}$${\ displaystyle \ pi _ {2} \ colon E_ {2} \ to B_ {2}}$${\ displaystyle f}$${\ displaystyle g}$ ${\ displaystyle \ pi _ {1} ^ {- 1} (\ {x \}) \ til \ pi _ {2} ^ {- 1} (\ {g (x) \})}$

eksempel

Ser på distriktet som et mangfold, så tangenten fra isomorf til den trivielle vektorpakken . Homeomorfismen mellom basisrommene er identisk med den mellom de totale rommene ${\ displaystyle S ^ {1}}$${\ displaystyle TS ^ {1} \ til S ^ {1}}$${\ displaystyle S ^ {1}}$${\ displaystyle S ^ {1} \ times \ mathbb {R} \ til S ^ {1}}$

${\ displaystyle (e ^ {i \ theta}, ite ^ {i \ theta}) \ mapsto (e ^ {i \ theta}, t)}$

for og . ${\ displaystyle e ^ {i \ theta} \ i S ^ {1}}$${\ displaystyle t \ in \ mathbb {R}}$

Underbygg

Undervektorpakke

De fibre av vektoren bunten ved punktet er betegnet med. En undervektorbunt av vektorpakken består av et topologisk underområde som består av en familie av undervektorrom av , så det er en separat vektorpakke. ${\ displaystyle E_ {x}}$${\ displaystyle \ pi \ colon E \ to B}$${\ displaystyle x \ i B}$${\ displaystyle \ pi \ colon E \ to B}$${\ displaystyle U \ delmengde E}$ ${\ displaystyle U_ {x}}$${\ displaystyle E_ {x}}$${\ displaystyle \ pi _ {U} \ kolon U \ til B}$

Begrenset vektorpakke

De fibre av vektoren bunten ved punktet er igjen betegnet med og betegner et topologisk underrom. Den begrensede vektorpakken er definert av ${\ displaystyle E_ {x}}$${\ displaystyle \ pi \ colon E \ to B}$${\ displaystyle x \ i B}$${\ displaystyle D \ delsett B}$${\ displaystyle D}$${\ displaystyle \ pi _ {D} \ kolon E_ {D} \ til D}$

${\ displaystyle E_ {D}: = E | _ {D}: = \ bigcup _ {m \ in D} E_ {m} \ quad {\ text {and}} \ quad \ pi _ {D}: = \ pi | _ {D}}$.

Den begrensede vektorpakken er en uavhengig vektorpakke med hensyn til det topologiske underområdet . ${\ displaystyle D}$

Konstruksjoner med vektorbunter

Tilbaketrukket vektorpakke

For en vektorpakke og en kontinuerlig kartlegging er den tilbaketrukne vektorpakken ("pull-back" eller "induced bundle", se også returtransport ) definert som pakken over med total plass ${\ displaystyle \ pi \ colon E \ to B}$${\ displaystyle f \ colon B_ {1} \ to B}$${\ displaystyle B_ {1}}$

${\ displaystyle f ^ {*} E: = \ left \ {(b, e) \ in B_ {1} \ times E \ colon f (b) = \ pi (e) \ right \}}$

og projeksjon . Vektorromstrukturen er definert av . Man kan vise at dette igjen definerer en lokalt triviell vektorpakke. ${\ displaystyle \ pi _ {1} (b, e) = b}$${\ displaystyle t_ {1} (b, e_ {1}) + t_ {2} (b, e_ {2}) = (b, t_ {1} e_ {1} + t_ {2} e_ {2}) }$

Følgende gjelder kartleggingen definert av og for hver induserer en vektorromisomorfisme . ${\ displaystyle {\ hat {f}} (b, e) = e}$${\ displaystyle {\ hat {f}} \ kolon f ^ {*} E \ til E}$${\ displaystyle \ pi \ circ {\ hat {f}} = f \ circ \ pi _ {1}}$${\ displaystyle b \ i B_ {1}}$${\ displaystyle {\ hat {f}}}$ ${\ displaystyle \ pi _ {1} ^ {- 1} (b) \ to \ pi ^ {- 1} (f (b))}$

For hvert buntkart har man en isomorfisme , der kartet som tilhører er basene. ${\ displaystyle {\ hat {g}} \ kolon E_ {1} \ til E_ {2}}$${\ displaystyle E_ {1} = g ^ {*} E_ {2}}$${\ displaystyle g \ colon B_ {1} \ to B_ {2}}$${\ displaystyle {\ hat {g}}}$

Direkte produkt, Whitney sum, tensor produkt

For to pakker med vektorer er det direkte produktet definert som ${\ displaystyle \ pi _ {i} \ kolon E_ {i} \ til B_ {i}, i = 1,2}$

${\ displaystyle \ pi _ {1} \ times \ pi _ {2} \ colon E_ {1} \ times E_ {2} \ to B_ {1} \ times B_ {2},}$

hvor hver fiber er forsynt med vektorromsstrukturen som den direkte summen av vektorrommene og . ${\ displaystyle (\ pi _ {1} \ times \ pi _ {2}) ^ {- 1} (b_ {1}, b_ {2}) = \ pi _ {1} ^ {- 1} (b_ { 1}) \ times \ pi _ {2} ^ {- 1} (b_ {2})}$${\ displaystyle \ pi _ {1} ^ {- 1} (b_ {1})}$${\ displaystyle \ pi _ {2} ^ {- 1} (b_ {2})}$

Nå la oss være vektorbunter over samme base, så . Whitney-summen din blir deretter definert som en trukket pakke ved hjelp av den diagonale kartleggingen${\ displaystyle \ pi _ {1}, \ pi _ {2}}$${\ displaystyle B_ {1} = B_ {2} = B}$ ${\ displaystyle d \ kolon B \ til B \ ganger B}$

${\ displaystyle \ pi _ {1} \ oplus \ pi _ {2}: = d ^ {*} (\ pi _ {1} \ times \ pi _ {2})}$.

Så Whitney-summen er bare vektorpakken over hvis fiber er over den direkte summen . ${\ displaystyle B}$${\ displaystyle b \ in B}$${\ displaystyle \ pi _ {1} ^ {- 1} (b) \ oplus \ pi _ {2} ^ {- 1} (b)}$

Tilsvarende er det tensorprodukt definert som vektoren bunt hvis fiber er over den tensorprodukt . ${\ displaystyle \ pi _ {1} \ otimes \ pi _ {2}}$${\ displaystyle b \ in B}$ ${\ displaystyle \ pi _ {1} ^ {- 1} (b) \ otimes \ pi _ {2} ^ {- 1} (b)}$

Andre objekter i vektorpakker

skjære

Hvis et åpent delsett av , kalles en kartlegging ${\ displaystyle U}$${\ displaystyle B}$

${\ displaystyle s \ colon U \ rightarrow E | _ {U} \ ,,}$

som gjelder et kutt på over . Settet med alle kutt fra over danner et vektorrom. ${\ displaystyle \ pi \ circ s = \ operatorname {id} | _ {U}}$${\ displaystyle E}$${\ displaystyle U}$${\ displaystyle \ Gamma (U, E)}$${\ displaystyle E}$${\ displaystyle U}$

ramme

En ramme (engelsk ramme , fransk repère ) er en slags base av en vektorpakke . Det er n lineært uavhengige vektorer for hver fiber. Disse vektorene danner en base av fiberen ved hvert punkt . Dette betyr nøyaktig:

La være en vektorpakke med rangering og være en åpen delmengde av basisrommet. En lokal reper eller ramme over er en bestilt n-tuple . Det er en kutt i over for alle i , slik at en base av fiberen dannes for alle . Hvis man kan velge, snakker man om et globalt rammeverk. ${\ displaystyle \ pi \ colon E \ to B}$${\ displaystyle n}$${\ displaystyle U \ delmengde B}$${\ displaystyle E}$${\ displaystyle U}$${\ displaystyle (\ sigma _ {1}, \ ldots, \ sigma _ {n})}$${\ displaystyle \ sigma _ {i}}$${\ displaystyle E}$${\ displaystyle U}$${\ displaystyle (\ sigma _ {1} (p), \ ldots, \ sigma _ {n} (p))}$${\ displaystyle E_ {p}}$${\ displaystyle p \ i U}$${\ displaystyle U = B}$

Vektorpakker med tilleggsstrukturer

Differensierbar vektorpakke

Vær en vektorpakke. Hvis og er differensierbare manifolder, og hvis projeksjonen så vel som trivialiseringene er differensierbare, kalles vektorbunten differensierbar . Det sies å være glatt hvis manifoldene er glatte og kartleggingen kan differensieres et hvilket som helst antall ganger. ${\ displaystyle \ pi \ colon E \ to B}$${\ displaystyle E}$${\ displaystyle B}$ ${\ displaystyle \ pi}$${\ displaystyle \ psi}$

Holomorf vektorpakke

En holomorf vektorbunt er en kompleks vektorbunt over en kompleks manifold , slik at den totale plassen er en kompleks manifold og projeksjonen er en holomorf kartlegging . ${\ displaystyle \ pi \ colon E \ to M}$ ${\ displaystyle M}$${\ displaystyle E}$${\ displaystyle \ pi}$

G-vektorpakke

Vær en gruppe. Hvis og er G-mellomrom , så er en vektorpakke en G-vektorpakke hvis gruppeaksjonen ${\ displaystyle G}$${\ displaystyle E}$${\ displaystyle B}$ ${\ displaystyle \ pi \ colon E \ to B}$

${\ displaystyle g \ colon E_ {x} \ rightarrow E_ {gx}}$

er et lineært kart for alle .${\ displaystyle g \ i G, x \ i B}$

Klassifisering av plass og klassifisering av bilde

Den klassifiserings plass for dimensjonale reelle vektorbunter er det Grassmann manifold av dimensjonale underrom i , dette blir kalt. Det betyr: hver -dimensjonale reelle vektorpakke er av form for en kontinuerlig kartlegging (den såkalte klassifiserende kartleggingen av bunten) og den tautologiske bunten , og to bunter er isomorfe hvis og bare hvis deres klassifiserende kartlegginger er homotopiske . ${\ displaystyle k}$${\ displaystyle k}$${\ displaystyle \ mathbb {R} ^ {\ infty}}$${\ displaystyle BO (k)}$${\ displaystyle k}$${\ displaystyle E \ til B}$${\ displaystyle f ^ {*} \ gamma ^ {k}}$${\ displaystyle f \ kolon M \ til BO (k)}$ ${\ displaystyle \ gamma ^ {k} \ til BO (k)}$

Analogt , Graßmann-manifolden til -dimensjonale delområder i , klassifiseringsrommet for -dimensjonale komplekse vektorbunter. ${\ displaystyle BU (k)}$${\ displaystyle k}$${\ displaystyle \ mathbb {C} ^ {\ infty}}$${\ displaystyle k}$

Stabile vektorbunter

To vektorbunter og kalles stabilt ekvivalent hvis det er trivielle vektorbunter (ikke nødvendigvis av samme dimensjon) med ${\ displaystyle E \ til B}$${\ displaystyle F \ til B}$${\ displaystyle G \ til B, H \ til B}$

${\ displaystyle E \ oplus G \ cong F \ oplus H}$

gir. Ekvivalensklassene til denne ekvivalensforholdet kalles stabile vektorbunter . (Denne definisjonen er ikke relatert til begrepet stabile vektorbunter i algebraisk geometri.)

La og de stigende assosiasjonene (dvs. colimittene med hensyn til inneslutningene definert ved hjelp av og ), så kan man vurdere en vektorpakke og dens klassifiserende kartlegging eller sammensetningen med inkluderingen eller . To vektorbunter er stabile ekvivalente hvis og bare hvis de tilsvarende tilordningene er homotopiske. ${\ displaystyle BO = \ cup BO (k)}$${\ displaystyle BU = \ cup BU (k)}$${\ displaystyle Gr (k, 2k) \ delmengde Gr (k + 1,2k + 2)}$${\ displaystyle BO (k) \ delmengde BO (k + 1)}$${\ displaystyle BU (k) \ delmengde BU (k + 1)}$${\ displaystyle E \ til B}$${\ displaystyle B \ til BO (k)}$${\ displaystyle B \ til BU (k)}$${\ displaystyle BO (k) \ to BO}$${\ displaystyle BU (k) \ to BU}$${\ displaystyle B \ til BO}$${\ displaystyle B \ to BU}$

Vektorbunter i algebraisk geometri

definisjon

For (algebraiske) vektorbunter i algebraisk geometri er og skjemaer , er for alle punktene i et vektorrom, og den lokale trivialiseringen er isomorfier ${\ displaystyle E}$${\ displaystyle B}$ ${\ displaystyle E_ {x}}$${\ displaystyle x}$${\ displaystyle B}$${\ displaystyle \ kappa (x)}$

${\ displaystyle U \ ganger A ^ {n} \ til E | _ {U}}$

I algebraisk geometri betyr imidlertid "vektorpakke" vanligvis en lokalt fri skive (se nedenfor).

Lokalfri skive

La det være et lokalt lite rom, f.eks. B. et topologisk rom med skiven av kontinuerlige reelle eller sammensatte verdier, en differensierbar manifold med funksjonskiven eller et skjema . ${\ displaystyle (X, O_ {X})}$${\ displaystyle C ^ {\ infty}}$

En lokalt fri skive er en - modul , den lokalt isomorfe til en fri er modul d. H. kan dekkes av åpne sett som er isomorf til en direkte sum av kopier av . ${\ displaystyle O_ {X}}$ ${\ displaystyle M}$${\ displaystyle O_ {X}}$${\ displaystyle X}$${\ displaystyle U}$${\ displaystyle M | _ {U}}$${\ displaystyle O_ {X} | _ {U}}$

Lokalfrie skiver og vektorbunter

Når det gjelder topologiske mellomrom eller differensierbare manifolder, gir de to følgende konstruksjonene en ekvivalens av kategoriene lokalt frie skiver og vektorknipper (for enkelthets skyld er tilfellet med reelle vektorbunter beskrevet over et topologisk rom) : ${\ displaystyle X}$

• Kappen av kuttene er tilordnet en vektorpakke.
• Den usammenhengende foreningen av fibrene tildeles en lokal fri skive . Vi velger en åpen dekning av , slik at hver enkelt blir triviell. En trivialisering definerer ingen steder forsvinnende kutt fra over , hvilke fiber av fiber danner en base. Disse definerer en kartlegging${\ displaystyle M}$${\ displaystyle E}$${\ displaystyle M_ {x} / m_ {x} M_ {x}}$${\ displaystyle (U_ {i})}$${\ displaystyle X}$${\ displaystyle M}$${\ displaystyle U_ {i}}$${\ displaystyle n}$${\ displaystyle M}$${\ displaystyle U_ {i}}$

${\ displaystyle U_ {i} \ times \ mathbb {R} ^ {n} \ til E}$,

og vi definerer topologien ved å kreve at disse tilordningene er homeomorfier. Det er veldefinert fordi disse kartleggingene skiller seg ut over skjæringspunktet mellom to sett og bare ved en homeomorfisme (mer presist, en kontinuerlig varierende vektorromautomisme av ).${\ displaystyle E}$${\ displaystyle U_ {i}}$${\ displaystyle U_ {j}}$${\ displaystyle \ mathbb {R} ^ {n}}$

Når det gjelder algebraisk geometri, er denne utformingen noe enklere: bunten til en lokalt fri skive er ${\ displaystyle E}$

${\ displaystyle {\ bf {V}} (E ^ {eller}): = {\ bf {Spec}} S (E ^ {eller})}$

her betegner den symmetriske algebra og den algebra spektrum . ${\ displaystyle S}$${\ displaystyle {\ bf {Spec}}}$

Ytterligere vilkår

• Undersøkelsen av såkalte stabile ekvivalensklasser av vektorbunter er gjenstand for K-teori .
• På algebraiske kurver har (semi) stabile vektorbunter spesielt gode egenskaper.

litteratur

• R. Abraham, JE Marsden , T. Ratiu: Manifolds, Tensor Analysis, and Applications . 2. utgave. Springer, Berlin 1988, ISBN 3-540-96790-7 (engelsk). 
• Allen Hatcher: Vector Bundles & K-Theory. Versjon 2.1, mai 2009, (math.cornell.edu; PDF; 1.11 MB) .
• Karlheinz Knapp: vektorpakke . Springer Fachmedien, Wiesbaden 2013, ISBN 978-3-658-03113-8 . 

weblenker

Individuelle bevis

1. ^ Thomas Friedrich: Dirac-operatører i Riemannian geometri . 1. utgave. Vieweg, 1997, ISBN 3-528-06926-0 . 
2. ↑ John Baez , Javier P. Muniain: Målerfelt, knuter og tyngdekraft (= Serien på knuter og alt. 4). World Scientific, Singapore et al. 1994, ISBN 981-02-2034-0 , s. 200.
3. ↑ Graeme Segal: Equivariant K-theory ( Memento fra 22. juni 2010 i Internet Archive )