Harmonisk oscillator

En harmonisk oscillator er et system som kan svinge , som er preget av en lineær tilbakestillingsvariabel . For et mekanisk system betyr dette at det er en kraft som motvirker en økende avbøyning med proporsjonalt økende styrke. Etter en ekstern impuls, svinger en harmonisk oscillator sinusformet (= harmonisk ) rundt hvileposisjonen , og svingningens varighet er uavhengig av størrelsen på nedbøyningen. Eksempler på harmoniske oscillatorer er fjærpendler , elektriske oscillerende kretser og tuning gafler .

Den harmoniske oscillatoren er et viktig modellsystem i fysikk. Det er fullstendig beskrevet av bare to parametere , den naturlige frekvensen og dempingen . Mange mer komplekse systemer oppfører seg omtrent som harmoniske oscillatorer med små nedbøyninger, f.eks. B. trådpendelen . Den harmoniske oscillatoren i kvantemekanikk er et av få kvantemekaniske systemer som kan beregnes uten tilnærminger.

Begrepet harmonisk oscillator brukes også om dempede harmoniske oscillatorer , selv om de strengt tatt ikke utfører en harmonisk svingning, men en dempet svingning .

Differensialligning av den harmoniske oscillatoren

Matematisk kan hver gratis harmoniske oscillator beskrives av følgende differensialligning . Unntak er oscillatorer i kvantemekanikk og relaterte teorier, der usikkerhetsrelasjoner må tas i betraktning.

${\ displaystyle {\ ddot {x}} + \ omega _ {0} ^ {2} \, x = 0}$

Dette inkluderer den avbøyning av systemet og den resonansfrekvens . Det er en vanlig, lineær , homogen differensialligning av andre orden, som derfor lett kan løses analytisk. Løsningen på en slik ligning er en sinusformet funksjon. ${\ displaystyle x (t)}$${\ displaystyle \ omega _ {0}}$${\ displaystyle x (t)}$

Harmonisk oscillatorpotensial

Potensialet V for en endimensjonal harmonisk oscillator

Den udempede harmoniske oscillatoren er et konservativt system. Dette betyr at energien til vibrasjonen beholdes. Det er derfor et potensial for hvert oscillatorkraftfelt .

Endimensjonal oscillator

Den grafiske fremstillingen av potensialet til en harmonisk oscillator er en parabel . Det kalles også harmonisk potensial. ${\ displaystyle V}$

${\ displaystyle V (x) = {\ frac {1} {2}} kx ^ {2}}$med målestokken ${\ displaystyle k> 0}$

I mekanikk er kraften på en partikkel i et slikt potensial gitt av det negative derivatet av potensialet. ${\ displaystyle F}$

${\ displaystyle F = - {\ frac {\ mathrm {d} V} {\ mathrm {d} x}} = - kx}$

Flerdimensjonal oscillator

Potensialet til en todimensjonal isotrop harmonisk oscillator

Dette konseptet kan brukes i flere dimensjoner . Potensialet her har form av en elliptisk paraboloid . I n dimensjoner kan det være et passende valg av koordinater som skriv dette:

${\ displaystyle V (x_ {1}, \ dotsc, x_ {n}) = {\ frac {1} {2}} \ sum _ {i = 1} ^ {n} k_ {i} \, x_ {i } ^ {2}}$

I mekanikk er kraften på en partikkel i et slikt potensial gitt av den negative gradienten av potensialet.

Fordi det ikke er blandede uttrykk mellom forskjellige retninger i de enkelte summander, kan problemet med en n- dimensjonal harmonisk oscillator reduseres til n endimensjonale oscillatorer. I kvantemekanikken kalles en slik egenskap separerbarhet . Det kan konkluderes med at med en harmonisk oscillator ikke bare den totale energien, men også energiene for komponentene i hver enkelt retning er konserverte størrelser.

Hvis potensialets verdi bare avhenger av avstanden til nullpunktet, men ikke av retningen, kalles oscillatoren isotrop , ellers anisotrop . Med en isotrop oscillator har alle konstanter samme verdi:

${\ displaystyle k_ {i} = c> 0 ~~~~~~~~ \ forall i = 1, \ ldots, n}$

og vibrasjoner i hver retning er harmoniske og har samme frekvens.

I en anisotropisk oscillator er vibrasjonene harmoniske i en enkelt koordinat og har en frekvens som avhenger av (normale vibrasjoner ). Hvis flere normale vibrasjoner blir begeistret med forskjellige , oppstår mer kompliserte, muligens også ikke-periodiske bevegelser. ${\ displaystyle x_ {i}}$${\ displaystyle k_ {i}}$${\ displaystyle k_ {i}}$

Minimum av potensial

Den minimum av dette potensialet er et stabilt fast punkt av systemet. I mekanikk kalles dette punktet også hvileposisjonen og kraften som partikkelen opplever, gjenopprettings- eller returkraften. Spesielt opplever en partikkel som ligger i hvileposisjonen ingen kraft, som navnet "hvileposisjon" er avledet fra. Navngivningen er litt misvisende i denne forbindelse: Selv om ingen kraft virker på en partikkel i hvilestilling, trenger ikke partikkelen å være i ro der. Generelt antar den til og med sin maksimale hastighet der.

Viktigheten i fysikk

Kvadratisk tilnærming av potensialet for Lennard-Jones (12.6). Variabelen x tilsvarer avstanden u .

En ideell harmonisk oscillator der gjenopprettingskraften for store avbøyninger øker lineært med avbøyningen, eksisterer ikke i naturen. Likevel er konseptet av grunnleggende betydning for fysikken, siden ofte bare små avbøyninger av et objekt fra hvileposisjonen blir vurdert. Hvis man begrenser seg til dette, kan potensialer som har et lokalt minimum erstattes til en god tilnærming med et harmonisk potensial, og hele problemet kan beskrives som en harmonisk oscillator. Fordelen med en slik harmonisk tilnærming er at problemet kan håndteres med standardmetoder for teoretisk fysikk og gir analytiske løsninger som er enkle å tolke. I figuren motsatt ble dette utført for et Lennard-Jones (12.6) potensial (blå kurve). Som man kan se, er resultatet (rød kurve) bare en nyttig tilnærming for små avstander fra minimumet.

Den harmoniske tilnærmingen finner sin matematiske begrunnelse i det faktum at potensialene kan utvikles i en Taylor-serie . Hvis et potensial blir gitt, og hvis det ofte er tilstrekkelig differensierbart, ifølge Taylor's teorem : ${\ displaystyle V}$

${\ displaystyle V (x) = V (x_ {0}) + {\ frac {\ partial V} {\ partial x}} (x_ {0}) (x-x_ {0}) + {\ frac {1 } {2}} {\ frac {\ partial ^ {2} V} {\ partial x ^ {2}}} (x_ {0}) (x-x_ {0}) ^ {2} + R (x- x_ {0})}$

hvor den såkalte resten bare inneholder vilkår fra tredje ordre. Det er derfor ubetydelig for små avstander . Som et utviklingspunkt velger vi et minimum av potensialet slik det gjelder . Førsteordensbetegnelsen er derfor også utelatt. For bedre matematisk manipulering kan ved en hensiktsmessig koordinattransformasjon av toppunktet tilsettes til opphavet til koordinater, slik at det følgende gjelder: . Videre er det alltid mulig å satse. Det omtrentlige harmoniske potensialet oppnås deretter: ${\ displaystyle R (x-x_ {0})}$${\ displaystyle x-x_ {0}}$${\ displaystyle x_ {0}}$${\ displaystyle {\ tfrac {\ partial V} {\ partial x}} (x_ {0}) = 0}$${\ displaystyle x_ {0} = 0}$${\ displaystyle V (x_ {0}) = 0}$

${\ displaystyle V (x) = {\ frac {1} {2}} kx ^ {2}}$ Med ${\ displaystyle k = {\ frac {\ partial ^ {2} V} {\ partial x ^ {2}}} (x_ {0})}$

Dette betyr at hvis nedbøyningen er tilstrekkelig liten, oppfører oscillatoren seg harmonisk. Et eksempel på oscillatorer som blir anharmoniske selv ved middels amplituder er trådpendelen .

En tilnærmet løsningsmetode, der et komplisert problem først reduseres til en analytisk løselig, for deretter å legge til tidligere ignorerte påvirkninger i form av forstyrrelser i løsningen, kalles forstyrrelsesteori .

Den harmoniske oscillatoren til klassisk mekanikk

Endimensjonal, ikke-dempet oscillator

En mekanisk oscillator består av en masse masse og en kraft som driver den tilbake når den avbøyes fra hvilestilling. For at en oscillator skal være harmonisk, må gjenopprettingskraften være proporsjonal med denne avbøyningen, dvs. kroppens avstand fra hvilestillingen. I praksis blir en slik kraft vanligvis implementert av fjærer , slik det er tilfelle med en fjærpendel , eller av kroppens vekt , slik det er for eksempel med en vannpendel .

Beskrivelse av oscillasjonsprosessen

Representasjon av svingningen til en harmonisk oscillator ved hjelp av eksemplet på en fjærpendel. Hvilestillingen til oscillatoren er markert med en stiplet linje. Hastigheten er merket som en rød pil

En harmonisk oscillator flyttes ut av hvilestillingen. Jo lenger du flytter den vekk, jo større krefter prøver å trekke den tilbake. Avbøyningen tilfører potensiell energi til oscillatoren . Betyr potensielt at energien brukes til å spenne en fjær, for eksempel, og denne energien lagres derfor i oscillatorposisjonen.

Hvis oscillatoren så slippes, akselereres den på grunn av vårens strekkraft. Den beveger seg derfor tilbake til hvileposisjonen med økende hastighet. Når den kommer dit, har oscillatoren nådd sin maksimale hastighet. Fjæren er avslappet, og det virker ikke lenger noen kraft som virker på oscillatoren. Den potensielle energien som ble matet til den er nå fullstendig omgjort til kinetisk energi . Dette betyr at den ikke lenger lagres i posisjonen, men i oscillatorens hastighet.

På grunn av treghet fortsetter imidlertid oscillatoren å bevege seg. Dette fører til at våren blir spent igjen, denne gangen i en annen retning. For å spenne denne våren, må oscillatoren bruke sin kinetiske energi for å kunne bevege seg mot fjærens kraft. Den bremser til den når det punktet der den ikke lenger beveger seg og all energien igjen er i form av potensiell energi. Bevegelsessekvensen starter deretter på nytt.

tid	Avbøyning ${\ displaystyle x}$	potensiell energi ${\ displaystyle {\ frac {k} {2}} x ^ {2}}$	hastighet ${\ displaystyle {\ dot {x}}}$	kinetisk energi ${\ displaystyle {\ frac {m} {2}} {\ dot {x}} ^ {2}}$
1	${\ displaystyle 0}$	${\ displaystyle 0}$	${\ displaystyle {\ sqrt {2E / m}}}$	${\ displaystyle E}$
2	${\ displaystyle {\ sqrt {2E / k}}}$	${\ displaystyle E}$	${\ displaystyle 0}$	${\ displaystyle 0}$
3	${\ displaystyle 0}$	${\ displaystyle 0}$	${\ displaystyle - {\ sqrt {2E / m}}}$	${\ displaystyle E}$
4. plass	${\ displaystyle - {\ sqrt {2E / k}}}$	${\ displaystyle E}$	${\ displaystyle 0}$	${\ displaystyle 0}$
uforanderlig: total energi , masse og vårkonstant${\ displaystyle E}$${\ displaystyle m}$${\ displaystyle k}$

Derivasjon av svingningsligningen

Illustrasjon av de fysiske mengdene av en vårpendel. Kraften vises som en grønn pil

Som ovenfor tar vi en vårpendel som et eksempel. Massa av kroppen er . Vi tar hvileposisjonen som nullpunkt og betegner avbøyningen med . Kraften som virker på kroppen er beskrevet av Hookes lov : ${\ displaystyle m}$${\ displaystyle x}$${\ displaystyle F}$

${\ displaystyle F = -kx}$

Konstanten er en fjærkonstant som avhenger av styrken til gjenopprettingskraften i tilfelle en fast avbøyning. Det er også kjent at akselerasjonen til et legeme er proporsjonal med kraften som virker på det. Akselerasjonen kan skrives som det andre avledede av stedet når det gjelder tid. Et tidsderivat blir ofte identifisert i fysikken som et punkt over variabelen: ${\ displaystyle k}$${\ displaystyle x}$

${\ displaystyle F = m {\ ddot {x}}}$

Hvis man nå likestiller disse to uttrykkene for kraften , får man en differensialligning: ${\ displaystyle F}$

${\ displaystyle m {\ ddot {x}} = - kx}$

For å forenkle følgende beregninger, erstatt og skriv ligningen på nytt: ${\ displaystyle \ omega _ {0} ^ {2} = {\ frac {k} {m}}}$

${\ displaystyle {\ ddot {x}} + \ omega _ {0} ^ {2} x = 0}$

Denne ligningen kan løses ved å bruke en eksponentiell tilnærming, for eksempel . Resultatet er en sinusformet funksjon, også kalt harmonisk svingning:

${\ displaystyle x (t) = u \, \ sin (\ omega _ {0} t + \ varphi)}$.

Løsningen inneholder to konstanter, amplituden og faseforskyvningsvinkelen . De oppnås i henhold til de opprinnelige forholdene . Amplituden står for maksimal nedbøyning av oscillatoren og dermed svingningens energi. Faseskiftvinkelen bestemmer posisjonen og samtidig hastigheten som kroppen har på den tiden . ${\ displaystyle u}$ ${\ displaystyle \ varphi}$${\ displaystyle t = 0}$

Sinusfunksjonen er en periodisk funksjon fordi verdiene gjentas med jevne mellomrom ( ). Derfor utfører oscillatoren en periodisk bevegelse. betegner den naturlige vinkelfrekvensen og resonansfrekvensen til oscillatoren. Den bestemmer frekvensen som oscillatoren oscillerer med. Når det gjelder en harmonisk oscillator, er denne frekvensen uavhengig av oscillasjonsamplituden. ${\ displaystyle \ sin (x) = \ sin (x + 2 \ pi)}$${\ displaystyle \ omega _ {0}}$${\ displaystyle f = {\ frac {\ omega _ {0}} {2 \ pi}}}$

energi

Med den frie, ikke-dempede oscillatoren beholdes energien fordi det er et lukket system og bare konservative krefter oppstår. I likevektsposisjon forsvinner den potensielle energien. Derfor er den totale energien lik den maksimale kinetiske energien:

${\ displaystyle E _ {\ text {total}} = {\ hat {E}} _ {\ text {kin}} = {\ frac {1} {2}} m {\ hat {v}} ^ {2 } = {\ frac {1} {2}} m \ omega ^ {2} {\ hat {x}} ^ {2}}$

Samme resultat kan oppnås hvis den totale energien beregnes ved å bruke den maksimale verdien av den potensielle energien:

${\ displaystyle E _ {\ text {total}} = {\ hat {E}} _ {\ text {pot}} = {\ frac {1} {2}} k {\ hat {x}} ^ {2 } = {\ frac {1} {2}} m {\ sqrt {\ frac {k} {m}}} ^ {2} {\ hat {x}} ^ {2} = {\ frac {1} { 2}} m \ omega ^ {2} {\ hat {x}} ^ {2}}$.

${\ displaystyle {\ hat {x}}}$står her for den maksimale nedbøyningsverdien, dvs. for amplituden. Hvis komplekse tall brukes til beregningen, tar kvadratet av størrelsen på amplituden, som kan være kompleks , plassen til . ${\ displaystyle {\ hat {x}} ^ {2}}$

Endimensjonal dempet oscillator

svak, lineært dempet svingning av en harmonisk oscillator

En mekanisk vibrasjon er generelt ikke friksjonsfri. Dette betyr at oscillasjonen mister energi gjennom friksjon og derfor reduseres amplituden. Man snakker om demping av svingningen, som et resultat av at den generelt ikke lenger er harmonisk. Et slikt system er ikke lenger konservativt , men avledende . I differensialligning, en friksjonskraft F _{R er} tilsatt til den akselererende kraft F.

${\ displaystyle m {\ ddot {x}} (t) = - kx (t) + F _ {\ mathrm {R}}}$

Kraftens tegn er motsatt hastigheten. Det eksakte uttrykket for F _R avhenger av typen friksjon. Mengden F kan være konstant eller for eksempel ha en lineær eller kvadratisk avhengighet av hastigheten.

I tilfellet med glidende friksjon , er mengden av F _{R er} konstant:

${\ displaystyle F _ {\ mathrm {R}} = - d \ operatorname {sgn} \ left ({\ dot {x}} (t) \ right)}$

Et eksempel på en lineær avhengighet er luftfriksjonen ved lave hastigheter. Der kan luftstrømmen sees på som laminær . I følge Stokes 'lov er den således proporsjonal med hastigheten, dvs. den første gangen som er avledet av avbøyningen.

${\ displaystyle F _ {\ mathrm {R}} = - d {\ dot {x}} (t)}$

I tilfelle en slik lineær demping kalles proporsjonalitetsfaktoren dempekonstanten . ${\ displaystyle d}$

Lineær demping

Når det gjelder lineær demping, kan friksjonen generelt tilsettes med et dempningsbegrep som er proporsjonalt og motsatt hastigheten . Konstanten er også kjent som forfallskonstanten . Dette gir bevegelsesligningen til en lineær dempet svingning som en vanlig lineær differensialligning av andre rekkefølge: ${\ displaystyle F _ {\ mathrm {R}} = - 2m \ gamma {\ dot {x}}}$${\ displaystyle {\ dot {x}}}$${\ displaystyle \ gamma \ geq 0}$

${\ displaystyle {\ ddot {x}} (t) +2 \ gamma {\ dot {x}} (t) + \ omega _ {0} ^ {2} x (t) = 0}$.

${\ displaystyle \ omega _ {0}}$betegner oscillatorens udampede naturlige vinkelfrekvens. En eksponentiell tilnærming fører til den generelle løsningen ${\ displaystyle x (t) = e ^ {\ lambda t}}$

${\ displaystyle x (t) = e ^ {- \ gamma t} \ left (c_ {1} e ^ {{\ sqrt {\ gamma ^ {2} - \ omega _ {0} ^ {2}}} t } + c_ {2} e ^ {- {\ sqrt {\ gamma ^ {2} - \ omega _ {0} ^ {2}}} t} \ right)}$

Her og komplekse verdsatte konstanter bestemmes ut fra de opprinnelige forholdene. ${\ displaystyle c_ {1}}$${\ displaystyle c_ {2}}$

• Ved svak demping ( ), som i det ikke-dempede tilfellet, oppstår en sinusformet svingning, hvis amplitude imidlertid faller eksponentielt. Styrken til dette fallet bestemmes av eksponenten til den omsluttende eksponensielle funksjonen: Amplituden synker til den opprinnelige amplituden over perioden. Vinkelfrekvensen til svingningen er redusert til .${\ displaystyle \ gamma <\ omega _ {0}}$${\ displaystyle \ gamma}$${\ displaystyle \ tau = 1 / \ gamma}$${\ displaystyle 1 / e}$${\ displaystyle \ omega _ {d} = {\ sqrt {\ omega _ {0} ^ {2} - \ gamma ^ {2}}}}$
• I tilfelle sterk demping ( ), det såkalte krypfallet , utvikler det seg ingen reell svingning. Snarere kryper avbøyningen mot hvileposisjonen.${\ displaystyle \ gamma> \ omega _ {0}}$
• I aperiodisk grensesak ( ) når oscillasjonen fortsatt en maksimal avbøyning ( ), men faller deretter tilbake til hvilestillingen raskere enn ved sterk demping. Hvorvidt en nullovergang finner sted, avhenger av de innledende forholdene.${\ displaystyle \ gamma = \ omega _ {0}}$${\ displaystyle t = \ tau}$

Hvis de innledende forholdene og tidspunktet er gitt, oppnås partikkeloppløsningen i tilfelle svingning${\ displaystyle x (0)}$${\ displaystyle {\ dot {x}} (0)}$${\ displaystyle t = 0}$${\ displaystyle \ omega _ {0} ^ {2} - \ gamma ^ {2}> 0}$

${\ displaystyle x (t) = e ^ {- \ gamma t} \ left (x (0) \ cdot \ cos (\ omega _ {d} t) + \ left (x (0) \ cdot \ gamma + { \ dot {x}} (0) \ right) {\ frac {\ sin (\ omega _ {d} t)} {\ omega _ {d}}} \ right)}$

Med ${\ displaystyle \ omega _ {d} ^ {2} = \ omega _ {0} ^ {2} - \ gamma ^ {2}}$

For det spesielle tilfellet , d. H. uten demping, er løsningen også forenklet ${\ displaystyle \ gamma = 0}$

${\ displaystyle x (t) = x (0) \ cdot \ cos (\ omega _ {0} t) + {\ dot {x}} (0) {\ frac {\ sin (\ omega _ {0} t )} {\ omega _ {0}}}}$

For aperiodic borderline case resultater ${\ displaystyle \ omega _ {0} ^ {2} - \ gamma ^ {2} = 0}$

${\ displaystyle x (t) = \ left (\ left ({\ dot {x}} (0) + \ gamma \ cdot x (0) \ right) \ cdot t + x (0) \ right) e ^ { - \ gamma t}}$

Variant: torsjonsoscillator

Torsjonsoscillatoren er en variant av den klassiske harmoniske oscillatoren.I stedet for en spiralfjær brukes her en torsjonsfjær eller en torsjonstråd. I stedet for translasjonsbevegelser er det da rotasjonsbevegelser. I prinsippet utføres beregningen på samme måte. Bare massen erstattes av treghetsmomentet og hastigheten av vinkelhastigheten . ${\ displaystyle m}$ ${\ displaystyle I}$${\ displaystyle v = {\ dot {x}}}$ ${\ displaystyle \ omega = {\ dot {\ varphi}}}$

Beskrivelse i Hamilton dynamics

Den udempede harmoniske oscillatoren i faseområdet. Tre baner med utgangsbetingelser for forskjellige energier vises

Bevegelsesligningen til den harmoniske oscillatoren kan også utledes ved hjelp av Hamiltonian mekanikk . Som ovenfor vurderer vi en masse på en fjær med vårkonstanter . Den gener koordinere blir brukt. The Hamilton-funksjonen består av potensiell og kinetisk energi som følger: ${\ displaystyle m}$${\ displaystyle k}$${\ displaystyle x = q}$ ${\ displaystyle H}$

${\ displaystyle H = {\ frac {p ^ {2}} {2m}} + {\ frac {m \ omega _ {0} ^ {2} q ^ {2}} {2}}}$

Med de kanoniske ligningene

${\ displaystyle {\ dot {p}} = - {\ frac {\ partial H} {\ partial q}} = - m \ omega _ {0} ^ {2} q}$

${\ displaystyle {\ dot {q}} = {\ frac {\ partial H} {\ partial p}} = {\ frac {p} {m}}}$

man kommer til bevegelsesligningen som allerede er beskrevet ovenfor.

${\ displaystyle {\ ddot {q}} + \ omega _ {0} ^ {2} q = 0}$

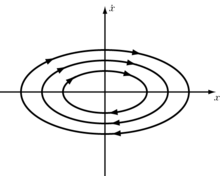
Siden den totale energien er bevart ( ), danner posisjonen og momentum en ellipse med halvakser og . ${\ displaystyle E}$${\ displaystyle {\ frac {\ partial H} {\ partial t}} = 0}$${\ displaystyle q}$${\ displaystyle p}$${\ displaystyle a}$${\ displaystyle b}$

${\ displaystyle {\ frac {p ^ {2}} {2mE}} + {\ frac {q ^ {2}} {2E / (m \ omega _ {0} ^ {2})}} = 1 = { \ frac {p ^ {2}} {a ^ {2}}} + {\ frac {q ^ {2}} {b ^ {2}}}}$

Systemets totale energi er proporsjonal med området som er omsluttet av ellipsen ${\ displaystyle A = \ pi \ cdot a \ cdot b = 2 \ pi E / \ omega _ {0}}$

I tilfelle av en dempet oscillator, i stedet for en ellipse , danner banen en spiral som beveger seg mot opprinnelsen.

Når det gjelder en flerdimensjonal harmonisk oscillator, kan hovedaksetransformasjonen og potensialets hovedakser brukes til å velge. Med et slikt valg kobler bevegelsesligningene de enkelte retningene. ${\ displaystyle q_ {i}}$${\ displaystyle p_ {i}}$

Flerdimensjonal oscillator

Representasjon av kraftfeltet til en isotrop harmonisk oscillator i to dimensjoner. Kraften er symbolisert med røde piler. Hvilestillingen er markert som et blått punkt.

For eksempel, med en Hamilton-tilnærming som forklart i forrige avsnitt, kan kraftloven for en n-dimensjonal harmonisk oscillator formuleres som:

${\ displaystyle m {\ ddot {\ mathbf {x}}} = - \ sum _ {i = 1} ^ {n} k_ {i} \ x_ {i} \, \ mathbf {e} _ {i} \ ,.}$

Du kan se at differensiallikningene er frakoplet, dvs. kraftkomponenten i en dimensjon avhenger bare av avbøyningen i denne dimensjonen. Derfor er løsningene for de enkelte komponentene i posisjonsvektoren løsningene for det tilsvarende endimensjonale problemet:

${\ displaystyle x_ {i} (t) = u_ {i} \, e ^ {\ lambda _ {i} \, t} + v_ {i} \, e ^ {- \ lambda _ {i} \, t }}$

Egenverdiene tilsvarer egencirkelfrekvensene. Hvis alt kan skrives som heltallmultipler av en konstant, er svingningen av den harmoniske oscillatoren periodisk. En isotrop harmonisk oscillator er derfor alltid periodisk. ${\ displaystyle \ textstyle \ lambda _ {i} = \ mathrm {i} \, {\ sqrt {\ frac {k_ {i}} {m}}}}$${\ displaystyle \ lambda _ {i}}$

To-dimensjonal oscillator

Med en anisotrop to-dimensjonal harmonisk oscillator beveger partikkelen seg på en Lissajous-kurve . Bevegelsen er periodisk når frekvensene til vibrasjonene i en koordinat er i et rasjonelt forhold. Ellers er det aperiodisk, dvs. H. den går aldri tilbake til utgangsstatusen. Men det kommer så nært du vil.

Når det gjelder en isotrop todimensjonal harmonisk oscillator, degenererer Lissajous-kurven til en sirkel, en romlig fast rett linje eller en romlig fast ellipse. Et eksempel er den sfæriske pendelen med små nedbøyninger.

Ligningene av bevegelse er

${\ displaystyle {\ begin {array} {ll} {\ ddot {x}} & = - \ omega _ {0} ^ {2} \, x \\ {\ ddot {y}} & = - \ omega _ {0} ^ {2} \, y \ end {array}}}$

Den generelle løsningen kan skrives som:

${\ displaystyle {\ vec {r}} (t) = {\ begin {pmatrix} x (t) \\ y (t) \ end {pmatrix}} = {\ begin {pmatrix} c_ {1} \\ c_ {2} \ end {pmatrix}} \ cos (\ omega _ {0} t) + {\ begin {pmatrix} c_ {3} \\ c_ {4} \ end {pmatrix}} \ sin (\ omega _ { 0} t)}$,

der konstantene er gitt av startplasseringen og starthastigheten. I dette tilfellet er ruten rett. Hvis og og begge ikke er parallelle med hverandre, er det baner i form av en ellipse eller sirkel, hvis senter er hvilestillingen. ${\ displaystyle {\ begin {pmatrix} c_ {1} \\ c_ {2} \ end {pmatrix}} = {\ vec {r}} (0)}$${\ displaystyle {\ begin {pmatrix} c_ {3} \\ c_ {4} \ end {pmatrix}} = {\ vec {v}} (0) / \ omega _ {0}}$${\ displaystyle {\ vec {v}} (0) = {\ vec {0}}}$${\ displaystyle {\ vec {r}} (0) \ neq {\ vec {0}}}$${\ displaystyle {\ vec {v}} (0) \ neq {\ vec {0}}}$

For å bestemme mulige bevegelsesformer uttrykkes den generelle løsningen som:

${\ displaystyle {\ begin {pmatrix} x (t) \\ y (t) \ end {pmatrix}} = {\ begin {pmatrix} A_ {x} \, \ cos (\ omega _ {0} t- \ alfa _ {x}) \\ A_ {y} \, \ cos (\ omega _ {0} t- \ alpha _ {y}) \ end {pmatrix}}}$

med vilkårlige verdier for amplitudene og faseforskyvningene som skyldes de opprinnelige forholdene. Ulike baner kan dannes, som alle har opprinnelse som sentrum og krysses med samme frekvens: ${\ displaystyle A_ {x}, \, A_ {y}}$${\ displaystyle \ alpha _ {x}, \, \ alpha _ {y}}$

• For det er en lineær harmonisk svingning mellom punktene langs en rett linje som danner vinkelen med x-aksen .${\ displaystyle \ alpha _ {x} = \ alpha _ {y}}$${\ displaystyle \ textstyle \ pm {\ begin {pmatrix} A_ {x} \\ A_ {y} \ end {pmatrix}}}$${\ displaystyle \ arctan (\ alpha _ {y} / \ alpha _ {x})}$
• For det er en ellips med halvaksene i lengde eller parallelt med koordinataksene. Hvis da blir ellipsen en sirkel. Da er pendelen en konisk pendel (se ovenfor).${\ displaystyle \ alpha _ {x}, = 0, \ alpha _ {y} = 90 ^ {\ circ}}$${\ displaystyle A_ {x}}$${\ displaystyle A_ {y}}$${\ displaystyle A_ {x} = A_ {y}}$
• Generelt resulterer en ellipse for hvilken som helst amplitude , hvis halvakser avhenger av alle fire parametrene og er tilbøyelige til koordinataksene.${\ displaystyle \ alpha _ {x} \ neq \ alpha _ {y}}$${\ displaystyle A_ {x}, \, A_ {y}}$

Kompleks nummernotasjon

De to koordinatene kan bli en enkelt kompleks variabel

${\ displaystyle u = x + {\ text {i}} y}$

oppsummeres. Den differensial ligning gjelder da å ${\ displaystyle u}$

${\ displaystyle {\ ddot {u}} = - \ omega _ {0} ^ {2} \, u}$

med den generelle løsningen

${\ displaystyle u (t) = A {\ text {e}} ^ {\ rm {{i} \ omega _ {0} t}} + B {\ text {e}} ^ {- {\ text {i }} \ omega _ {0} t}}$.

De to konstantene er beregnet ut fra de opprinnelige forholdene: ${\ displaystyle A, \, B}$

${\ displaystyle {\ begin {array} {ll} u (0) = x (0) + {\ text {i}} \, y (0) = A + B \\ {\ dot {u}} (0 ) = {\ dot {x}} (0) + {\ text {i}} \, {\ dot {y}} (0) = {\ text {i}} \, \ omega _ {0} (AB ) \ end {array}}}$

Enkle spesielle tilfeller er:

• For det er en sirkelbane med klokken (matematisk negativ forstand) med en radius .${\ displaystyle B = 0}$${\ displaystyle R = | A |}$
• For det er en sirkelbane mot klokken (matematisk positiv forstand) med en radius .${\ displaystyle A = 0}$${\ displaystyle R = | B |}$
• For det er en rett linje mellom fra punkt til punkt (og bak).${\ displaystyle A = B \, (\ neq 0)}$${\ displaystyle {\ begin {pmatrix} 2 \, {\ text {Re}} (A) \\ 2 \, {\ text {Im}} (A) \ end {pmatrix}}}$${\ displaystyle {\ begin {pmatrix} -2 \, {\ text {Re}} (A) \\ - 2 \, {\ text {Im}} (A) \ end {pmatrix}}}$
• Den Resultatet er det samme rette linje, men starter i hvileposisjon.${\ displaystyle A = -B \, (\ neq 0)}$

Den harmoniske oscillatoren utenfor mekanikken

Elektrisk oscillerende krets

Kretsskjema over en elektrisk oscillerende krets

Den elektriske oscillerende kretsen er en harmonisk oscillator innen elektrodynamikk . Mens i mekanikk periodisk potensial og kinetisk energi blir omgjort til hverandre, byttes den elektriske energien som er lagret i en kondensator med kapasitansen og den magnetiske energien som er lagret i en spole med induktansen , i resonanskretsen . En differensialligning resulterer i strømstyrken : ${\ displaystyle C}$${\ displaystyle L}$${\ displaystyle i}$

${\ displaystyle {\ ddot {i}} (t) + {\ frac {1} {LC}} \, i (t) = 0}$

Likheten med bevegelsesligningen til den mekaniske oscillatoren er åpenbar. Tabellen nedenfor er ment å gjøre analogiene mellom mekanisk og elektrisk oscillator tydelig:

mekanisk (oversettelse)	mekanisk (torsjon / rotasjon)	RLC-serie resonanskrets	RLC parallell resonanskrets
Avbøyning ${\ displaystyle x}$	vinkel ${\ displaystyle \ varphi}$	lade ${\ displaystyle q}$	Spenninger ${\ displaystyle u}$
hastighet ${\ displaystyle {\ dot {x}} \ equiv v}$	Vinkelhastighet ${\ displaystyle {\ dot {\ varphi}} \ equiv \ omega}$	Strømstyrke ${\ displaystyle {\ dot {q}} \ equiv i}$	Spenningsendringshastighet ${\ displaystyle {\ dot {u}}}$
Dimensjoner ${\ displaystyle m}$	Treghetsmoment ${\ displaystyle I}$	Induktans ${\ displaystyle L}$	kapasitet ${\ displaystyle C}$
Vårrate ${\ displaystyle k}$	Torsjonskonstant ${\ displaystyle \ mu}$	Gjensidig kapasitet ${\ displaystyle 1 / C}$	Gjensidig induktans ${\ displaystyle 1 / L}$
Dempingskonstant ${\ displaystyle d}$	Dempingskonstant ${\ displaystyle \ Gamma}$	motstand ${\ displaystyle R}$	Ledningsevne ${\ displaystyle 1 / R}$
ytre kraft ${\ displaystyle F (t)}$	eksternt dreiemoment ${\ displaystyle M (t)}$	ekstern spenning ${\ displaystyle u_ {e} (t)}$	Endringshastighet i ekstern strøm ${\ displaystyle {\ dot {i}} _ {e} (t)}$
Ustemplet naturlig frekvens : ${\ displaystyle f_ {0}}$
${\ displaystyle {\ frac {1} {2 \ pi}} {\ sqrt {\ frac {k} {m}}}}$	${\ displaystyle {\ frac {1} {2 \ pi}} {\ sqrt {\ frac {\ mu} {I}}}}$	${\ displaystyle {\ frac {1} {2 \ pi}} {\ sqrt {\ frac {1} {LC}}}}$	${\ displaystyle {\ frac {1} {2 \ pi}} {\ sqrt {\ frac {1} {LC}}}}$
Differensial ligning
${\ displaystyle m {\ ddot {x}} + d {\ dot {x}} + kx = F (t)}$	${\ displaystyle I {\ ddot {\ varphi}} + \ Gamma {\ dot {\ varphi}} + \ mu \ varphi = M (t)}$	${\ displaystyle L {\ ddot {q}} + R {\ dot {q}} + q / C = u_ {e} (t)}$	${\ displaystyle C {\ ddot {u}} + {\ dot {u}} / R + u / L = {\ dot {i}} _ {e} (t)}$

Den harmoniske oscillatoren til kvantemekanikken

Siden ethvert potensial kan utvikles rundt en stabil likevektsposisjon og deretter er parabolsk i den første tilnærmingen, er den harmoniske oscillatoren en standardmodell i kvantemekanikk. Det er et av få system som en analytisk løsning er kjent for.

I kvantemekanikk blir posisjon, momentum og energivariabler for en partikkel erstattet av operatører . Hamilton-operatøren for energien til en harmonisk oscillator er gitt av

${\ displaystyle {\ hat {H}} = {\ frac {{\ hat {p}} ^ {2}} {2m}} + m \ omega ^ {2} {\ frac {{\ hat {x}} ^ {2}} {2}}}$.

De bølgefunksjoner med hvilken sannsynlighetene for partikkelens plassering kan beregnes er egenfunksjonene Hamilton operatør. Energinivået tilsvarer egenverdiene.

Lorentz oscillator i optikk

Den Lorentz oscillator blir brukt i optikk som en modell for å beskrive oppførselen til de atomer av en fast under påvirkning av en elektromagnetisk bølge. For eksempel er følsomheten , som motvirker oppbyggingen av feltet, den analoge av demping gjennom friksjon i mekanikken. Ved hjelp av Lorentz-oscillatoren kan optiske fenomener som dobbeltbrytning eller den komplekse brytningsindeksen forklares i Drude- modellen.

Eksitasjon av harmoniske oscillatorer

Når energi tilsettes en oscillator, kalles det stimulering. For den mekaniske oscillatoren betyr dette at enten en ekstern kraft virker eller parametere til oscillatoren, slik som den naturlige frekvensendringen . Excitasjonen av kvantemekaniske oscillatorer er representert ved hjelp av stigeoperatorer (se harmonisk oscillator (kvantemekanikk) ). Spredningen av energi, også kalt de-eksitasjon, skjer på samme måte. ${\ displaystyle F _ {\ mathrm {ext}}}$${\ displaystyle \ omega _ {0}}$

Tvunget vibrasjon

En tvungen svingning blir begeistret av en uavhengig, vanligvis periodisk kraft eller elektrisk spenning. Et eksempel på dette er en dipolantenne . Differensiallikningen, her eksemplet med den dempede oscillatoren, blir inhomogen:

${\ displaystyle {\ ddot {x}} (t) +2 \ gamma {\ dot {x}} (t) + \ omega _ {0} ^ {2} x (t) = {\ frac {F _ { \ mathrm {ext}} (t)} {m}}}$

Selvopphisset vibrasjon

Vi snakker om selvopprørt svingning når energiforsyningen styres av et passende kontrollelement og selve svingningsprosessen. Matematisk kan en slik energiforsyning realiseres, for eksempel gjennom et spesielt dempningsbegrep, der dempingen kan bli negativ. Et slikt system er stort sett ikke-lineært. Et eksempel på dette er van der Pol-oscillatoren .

Parameter-begeistret svingning

Hvis den naturlige frekvensen til en harmonisk oscillator endres over tid på grunn av en endring i parametere som lengden på en pendel , kalles dette en parameter-spent svingning. Et eksempel er en sving med små avbøyninger. ${\ displaystyle \ omega _ {0}}$

Koblede harmoniske oscillatorer

Med to pendler festet til en streng overføres svingningsenergien med jevne mellomrom mellom de to pendlene.

En flerdimensjonal harmonisk oscillator, der de enkelte komponentene, dvs. de harmoniske oscillatorene langs potensialets hovedakser, ikke er uavhengige, men samhandler med hverandre, kalles koblet. Dette betyr at energien til oscillasjonen av de enkelte komponentene ikke lenger trenger å beholdes, da den kan overføres fra en komponent til en annen gjennom interaksjonen. Dette skaper en form for amplitudemodulasjon .

Koblede mekaniske oscillatorer kalles også koblede pendler . En mekanisk interaksjon mellom to pendler opprettes for eksempel ved å koble massene til to separate pendler med en fjær. Hvis flere identiske pendler, ordnet på rad, hver er koblet til sine nærmeste naboer via fjærer, kalles arrangementet en svingkjede. Et interessant eksempel der energien veksler mellom en translasjonsbevegelse og en rotasjonsbevegelse er Wilberforce-pendelen .

Ved hjelp av koblede oscillatorer kan også gittervibrasjoner modelleres i krystaller . Her sørger den elektriske interaksjonen mellom ionene, molekylene eller atomene i krystallgitteret for nødvendig kobling. Den kvantemekaniske betraktningen i artikkelen Harmonic Oscillator (Quantum Mechanics) fører deretter til fononene .

Kontinuerlig overgang

Vibrasjoner i et kontinuum , for eksempel en strengvibrasjon, kan beskrives ved hjelp av en uendelig dimensjonalt koblet harmonisk oscillator eller et uendelig antall endimensjonale koblede harmoniske oscillatorer. Overgangen til et uendelig antall oscillatorer utføres deretter for en langsgående bølge. Metoden kan også utføres analogt for tverrbølger .

Skjema for en fjæroscillator med n koblede oscillatorer

Vi tar eksemplet med koblede oscillatorer av massen , som er forbundet med fjærer med fjærkonstanter . Vi betegner den avbøyning av i th oscillator med . Avstanden mellom de enkelte massene er . Den Lagrange funksjonen til dette systemet blir da: ${\ displaystyle n}$${\ displaystyle m}$${\ displaystyle k}$${\ displaystyle q_ {i}}$${\ displaystyle l}$

${\ displaystyle {\ mathcal {L}} = {\ frac {m} {2}} \ sum _ {i = 1} ^ {n} {\ dot {q}} _ {i} ^ {2} - { \ frac {k} {2}} \ sum _ {i = 0} ^ {n} (q_ {i + 1} -q_ {i}) ^ {2}}$

Systemets bevegelsesligning kan utledes av dette som:

${\ displaystyle m {\ ddot {q}} _ {i} = k ((q_ {i + 1} -q_ {i}) - (q_ {i} -q_ {i-1}))}$

Vi deler denne ligningen og får: ${\ displaystyle kl ^ {2}}$

${\ displaystyle {\ frac {m} {k \, l ^ {2}}} {\ ddot {q}} _ {i} = {\ frac {1} {l}} \ left ({\ frac {q_ {i + 1} -q_ {i}} {l}} - {\ frac {q_ {i} -q_ {i-1}} {l}} \ høyre)}$

En kontinuumovergang erstatter den diskrete indeksen med en kontinuerlig koordinat og den diskrete funksjonen med bølgefunksjonen . For en slik kontinuum grense er den samme grense , , og tas så gjør de følgende variable holdes konstant: ${\ displaystyle i}$${\ displaystyle x = i \ cdot l}$${\ displaystyle q_ {i} (t)}$${\ displaystyle \ Psi (x, t)}$ ${\ displaystyle n \ to \ infty}$${\ displaystyle l \ til 0}$${\ displaystyle m \ til 0}$${\ displaystyle k \ to \ infty}$

• Total lengde ${\ displaystyle (n + 1) l}$
• Den totale massen og dermed også tettheten${\ displaystyle nm}$${\ displaystyle m / l}$
• Produktet av vårkonstanten og fjærlengden ${\ displaystyle kl}$

Faktoren til venstre for ligningen er konstant. Derfor kan denne siden skrives som ${\ displaystyle {\ frac {m} {k \, l ^ {2}}}}$

${\ displaystyle {\ frac {1} {c ^ {2}}} {\ frac {\ partial ^ {2} \ Psi} {\ partial t ^ {2}}}}$

Høyre side av ligningen kan skrives om som:

${\ displaystyle \ lim _ {l \ to 0} {\ frac {1} {l}} \ left ({\ frac {\ Psi (x + l, t) - \ Psi (x, t)} {l} } - {\ frac {\ Psi (x, t) - \ Psi (xl, t)} {l}} \ right)}$

Dette er nettopp forskjellskvotienten for det andre derivatet . Man får nemlig um ved hjelp av en Taylor-utvidelse${\ displaystyle x}$

${\ displaystyle \ lim _ {l \ to 0} \ left ({\ frac {\ Psi (x + l, t) -2 \ Psi (x, t) + \ Psi (xl, t)} {l ^ { 2}}} \ right) = \ lim _ {l \ to 0} {\ frac {1} {l ^ {2}}} \ left ({\ frac {\ partial ^ {2} \ Psi} {\ partial x ^ {2}}} (x, t) \ cdot l ^ {2} + {\ mathcal {O}} (l ^ {4}) \ right) = {\ frac {\ partial ^ {2} \ Psi } {\ delvis x ^ {2}}} (x, t)}$

Den bølgelikningen blir således oppnådd

${\ displaystyle \ left ({\ frac {1} {c ^ {2}}} {\ frac {\ partial ^ {2}} {\ partial t ^ {2}}} - {\ frac {\ partial ^ { 2}} {\ delvis x ^ {2}}} \ høyre) \ Psi = 0}$

weblenker

• Harmonisk oscillator, kvantemekanisk
• ChemgaPedia om harmonisk / anharmonisk oscillator
• Detaljert avledning av løsningen for den dempede harmoniske oscillatoren .

Individuelle bevis

1. ^ Wolfgang Demtröder: Experimentalphysik 1 . 4. utgave. Springer, Berlin / Heidelberg 2006, ISBN 3-540-26034-X , s. 335-357 . 
2. ↑ Wolfgang Nolting: Teoretisk fysikk 2 . 7. utgave. Springer, Berlin / Heidelberg 2006, ISBN 3-540-30660-9 , pp. 103-104 . 

Merknader

1. ↑ Tidsinformasjon refererer til grafikken ovenfor; avstanden mellom to tidspunkter er en kvart periode, altså .${\ displaystyle {\ frac {\ pi} {2}} {\ sqrt {m / k}}}$