Denne artikkelen dekker multiplikasjonen av to vektorer, hvis resultat er en
skalar . For multiplikasjon av vektorer med skalarer, hvis resultat er en vektor, se
skalar multiplikasjon .
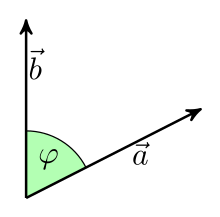
Det skalære produktet til to vektorer i det euklidiske
intuisjonsområdet avhenger av lengden på vektorene og den inkluderte vinkelen.
Den skalarproduktet (også indre produkt eller punkt produkt ) er en matematisk kombinasjon som tildeler et nummer ( skalar ) til to vektorer . Det er gjenstand for analytisk geometri og lineær algebra . Historisk sett ble den først introdusert i det euklidiske rommet . Geometrisk beregning av skalarproduktet til to vektorer og i henhold til formelen



Og betegne de lengder (mengder) av vektorer. Med er cosinus for vinkelen som er omsluttet av de to vektorene . Det skalære produktet til to vektorer med en gitt lengde er derfor null hvis de er vinkelrett på hverandre og maksimale hvis de har samme retning.




I et kartesisk koordinatsystem , skalarproduktet av to vektorer er og beregnes som



Hvis du kjenner de kartesiske koordinatene til vektorene, kan du bruke denne formelen til å beregne det skalære produktet, og deretter bruke formelen fra forrige avsnitt for å beregne vinkelen mellom de to vektorene ved å løse den for :



I lineær algebra er dette konseptet generalisert. Et skalarprodukt er en funksjon som tildeler en skalar til to elementer i et reelt eller komplekst vektorrom , nærmere bestemt en ( positivt bestemt ) hermitisk sesquilinær form , eller mer spesifikt i reelle vektorrom en (positivt bestemt) symmetrisk bilinær form . Generelt er ikke noe skalarprodukt definert fra starten i et vektorrom. Et rom sammen med et skalarprodukt kalles et indre produktrom eller et prehilbert-rom . Disse vektorområdene generaliserer det euklidiske rommet og muliggjør dermed anvendelse av geometriske metoder på abstrakte strukturer.
I det euklidiske rommet
Geometrisk definisjon og notasjon
Vektorer i tredimensjonalt euklidisk rom eller i det todimensjonale euklidiske planet kan representeres som piler. I dette tilfellet har filtrepilene parallelle samme lengde, og lik den samme vektoren. Punktproduktet til to vektorer , og er en skalar, det vil si et reelt tall. Geometrisk kan den defineres som følger:



Og betegner lengdene på vektorene og og betegner vinkelen som er omsluttet av, og det er det også








Som med normal multiplikasjon (men sjeldnere enn der), blir multiplikasjonstegnet noen ganger utelatt når det er klart hva som menes:

I stedet for å skrive av og til i dette tilfellet

Andre vanlige notasjoner er og

illustrasjon
For å illustrere definisjonen, vurder den ortogonale projeksjonen av vektoren i retningen gitt av og sett




Da og for det skalære produktet av og vi har:




Dette forholdet brukes noen ganger for å definere det skalære produktet.
Eksempler
I alle tre eksempler, og . De skalære produktene skyldes spesielle cosinusverdier , og :





I kartesiske koordinater
Hvis du introduserer kartesiske koordinater i det euklidiske planet eller i det euklidiske rommet, har hver vektor en koordinatrepresentasjon som en 2- eller 3-tupel, som vanligvis skrives som en kolonne.
I det euklidiske planet oppnår man deretter det skalære produktet av vektorene
-
 og
og 
representasjonen


Kanoniske enhetsvektorer i det euklidiske planet
For den kanoniske enhetsvektorene og den gjelder følgende:


-
 og
og 
Det følger av dette (forutse egenskapene til skalarproduktet forklart nedenfor):

I et tredimensjonalt euklidisk rom oppnår man tilsvarende for vektorene
-
 og
og 
representasjonen

For eksempel beregnes det skalære produktet til de to vektorene
-
 og
og 
som følger:

kjennetegn
Fra den geometriske definisjonen følger det direkte:
- Hvis og er parallelle og like orienterte ( ), gjelder det




- Spesielt er det skalære produktet til en vektor med seg selv kvadratet av lengden:

- Hvis og er orientert parallelt og motsatt ( ), gjelder det




- Hvis og er ortogonale ( ), så har vi det




- Hvis vinkelen er spiss, gjelder følgende


- Er en stump vinkel , følgende gjelder


Som en funksjon som tildeler det reelle tallet til hvert bestilt vektorpar , har skalarproduktet følgende egenskaper, som man forventer av en multiplikasjon:


- Det er symmetrisk (kommutativ lov):
-
 for alle vektorer og
for alle vektorer og

- Det er homogent i alle argumenter (blandet assosiativ lov):
-
 for alle vektorer og og for alle skalarer
for alle vektorer og og for alle skalarer


- Det er additiv i alle argumenter (distribusjonslov):
-
 og
og
-
 for alle vektorer og
for alle vektorer og


Egenskapene 2 og 3 er også oppsummert: Det skalære produktet er bilinært .
Betegnelsen "blandet assosiativ lov" for 2. egenskap gjør det klart at en skalar og to vektorer er koblet på en slik måte at parentesene kan byttes ut som i assosiativ lov. Siden skalarproduktet ikke er en indre lenke, defineres ikke et skalarprodukt av tre vektorer, så spørsmålet om ekte associativitet oppstår ikke. I uttrykket er bare den første multiplikasjonen et skalarprodukt av to vektorer, den andre er produktet av en skalar med en vektor ( S-multiplikasjon ). Uttrykket representerer en vektor, et multiplum av vektoren. På den annen side representerer uttrykket et multiplum av . Generelt





Verken den geometriske definisjonen eller definisjonen i kartesiske koordinater er vilkårlig. Begge følger av det geometrisk motiverte kravet om at skalarproduktet til en vektor med seg selv er kvadratet av lengden, og det algebraisk motiverte kravet om at skalarproduktet oppfyller egenskapene 1-3 ovenfor.
Mengde vektorer og vinkler inkludert
Ved hjelp av skalarproduktet er det mulig å beregne lengden (mengden) av en vektor fra koordinatrepresentasjonen:
Følgende gjelder en vektor med todimensjonalt rom


Man anerkjenner her den pytagoreiske teoremet . Det samme gjelder i tredimensjonalt rom

Ved å kombinere den geometriske definisjonen med koordinatrepresentasjonen, kan vinkelen de omslutter, beregnes fra koordinatene til to vektorer. Ute

følger

Lengden på de to vektorene
-
 og
og 
beløper seg til
-
 og
og 
Cosinus av vinkelen som er omsluttet av de to vektorene, beregnes som

Slik er det også 
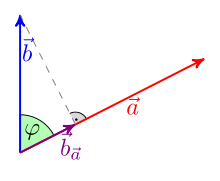
Orthogonalitet og ortogonal projeksjon
To vektorer og er ortogonale hvis og bare hvis deres skalære produkt er null, altså



Den ortogonale projeksjonen fra retningen gitt av vektoren er vektoren med




så

Projeksjonen er vektoren hvis sluttpunkt er loddlinjen fra sluttpunktet til den rette linjen gjennom nullpunktet bestemt av. Vektoren står loddrett



Hvis er en enhetsvektor (dvs. ist ), forenkles formelen til



Forhold til kryssproduktet
En annen måte å kombinere to vektorer og multiplisere dem i et tredimensjonalt rom er det ytre produktet eller kryssproduktet. I motsetning til det skalære produktet er resultatet av kryssproduktet ikke en skalar, men en vektor igjen. Denne vektor er perpendikulær på planet spennes ved de to vektorer og og dens lengde tilsvarer det område av det parallellogram som er dannet av dem.





Følgende beregningsregler gjelder for tilkoblingen av kryssproduktet og det skalære produktet:




Kombinasjonen av tverrproduktet og det skalære produktet av de to første reglene kalles også det sene produktet ; det gir det orienterte volumet av parallellpiped spennt av de tre vektorene .

applikasjoner
I geometri

Kosinosetning med vektorer
Det skalære produktet gjør det mulig å bare bevise kompliserte teoremer som snakker om vinkler.
Krav: ( cosinus lov )

Bevis: Ved hjelp av tegnet i vektorer følger det (Retningen er irrelevant.) Kvadrering av beløpet gir



og dermed

I fysikk
I fysikk er mange mengder , for eksempel arbeid , definert av skalære produkter:


med vektormengdene kraft og bane . Det betegner vinkelen mellom kraftens retning og banen. Med er komponenten av kraften i retning av banen, med komponenten av banen i retning av kraften.





Eksempel: En vogn av vekten transporteres over et skrått plan fra til . Løftearbeidet er beregnet





Generelt virkelige og komplekse vektorrom
Man tar ovennevnte egenskaper som en mulighet til å generalisere konseptet med skalarproduktet til alle reelle og komplekse vektorrom . Et skalarprodukt er da en funksjon som tildeler et kroppselement (skalar) til to vektorer og som oppfyller de nevnte egenskapene. I det komplekse tilfellet blir tilstanden til symmetri og bilinearitet endret for å lagre den positive definisjonen (som aldri oppfylles for komplekse symmetriske bilineære former).
Generelt sett er variablene for vektorer, dvs. elementer i et hvilket som helst vektorrom, generelt ikke indikert med piler. Det skalære produktet er vanligvis ikke betegnet med et malepunkt, men med et par vinkelfester. Så for det skalære produktet av vektorene og man skriver . Andre vanlige notasjoner er (spesielt i kvantemekanikk i form av Bra-Ket- notasjon), og .






Definisjon (aksiomatisk)
Et skalarprodukt eller indre produkt på et reelt vektorrom er en positivt bestemt symmetrisk bilinær form, det vil si for og følgende betingelser gjelder:




- lineær i hvert av de to argumentene:




- symmetrisk:

- positiv bestemt:

-
 nøyaktig når
nøyaktig når 
Et skalarprodukt eller indre produkt på et komplekst vektorrom er en positivt bestemt hermitisk sesquilinear form som betyr for og følgende forhold gjelder:




- sesquilinear:

-
 (halvlinje i første argument)
(halvlinje i første argument)

-
 (lineær i det andre argumentet)
(lineær i det andre argumentet)
- eremittisk:

- positiv bestemt:
-
 (Det er virkelig følger av betingelse 2.)
(Det er virkelig følger av betingelse 2.)
-
 nøyaktig når
nøyaktig når 
Et reelt eller komplekst vektorrom der et skalarprodukt er definert, kalles et skalarproduktrom eller Prähilbert-rom . Et endelig-dimensjonalt reelt vektorrom med skalarprodukt kalles også euklidisk vektorrom , i det komplekse tilfellet snakker man om et enhetlig vektorrom. Tilsvarende blir det skalære produktet i et euklidisk vektorrom av og til referert til som det euklidiske skalarproduktet, og det i et enhetsvektorrom som det enhetlige skalarproduktet . Uttrykket "Euklidisk skalarprodukt" men også spesielt for den ovenfor beskrevne geometriske skalar eller beskrevet nedenfor standard skalar i bruk.

- Merknader
- Ofte er hver symmetrisk bilinær form eller hver hermitisk sesquilinear form referert til som et skalarprodukt; Med denne bruken beskriver definisjonene ovenfor positivt bestemte skalarprodukter.
- De to aksiomsystemene som er gitt er ikke minimale. I det virkelige tilfellet, på grunn av symmetrien, følger lineariteten i det første argumentet fra lineariteten i det andre argumentet (og omvendt). På samme måte, i det komplekse tilfellet, på grunn av eremitisiteten, følger halvlineariteten i det første argumentet fra lineariteten i det andre argumentet (og omvendt).
- I det komplekse tilfellet blir det skalære produktet noen ganger definert alternativt, nemlig som lineært i første og halvlinje i det andre argumentet. Denne versjonen er foretrukket i matematikk og spesielt i analyse , mens den ovennevnte versjonen hovedsakelig brukes i fysikk (se Bra- og Ket-vektorer ). Forskjellen mellom de to versjonene ligger i effekten av skalar multiplikasjon når det gjelder homogenitet . Etter at den alternative versjonen gjelder for og og . Den additivitet er forstått på samme måte i begge versjoner. Normene oppnådd fra skalarproduktet i henhold til begge versjoner er også identiske.




- En pre-Hilbert rom, som helt i forhold til den som induseres ved den skalare standarden er referert til som den Hilbert plass , henholdsvis.
- Skillet mellom reelt og komplekst vektorrom når man definerer skalarproduktet er ikke absolutt nødvendig, siden en hermitisk sesquilinær form i realiteten tilsvarer en symmetrisk bilinær form.
Eksempler
Standard skalarprodukt i R n og i C n
Med utgangspunkt i representasjonen av det euklidiske skalarproduktet i kartesiske koordinater, definerer man standard skalarproduktet i -dimensjonalt koordinatrom for gjennomgående
i lineær algebra



Det “geometriske” skalarproduktet i det euklidiske rommet behandlet ovenfor tilsvarer spesialtilfellet. For det dimensjonale komplekse vektorområdet er standard skalarproduktet definert av





der overlinjen betyr den komplekse bøyningen . I matematikk brukes ofte den alternative versjonen, der det andre argumentet er konjugert i stedet for det første.
Standard skalarprodukt i eller kan også skrives som et matriksprodukt ved å tolke vektoren som en matrise ( kolonnevektor ): I virkeligheten gjelder følgende




hvor er radvektoren som er resultatet av kolonnevektoren ved transponering . I det komplekse tilfellet (for venstre halvlinje, høyre lineær sak)



hvor er den rad vektoren adjungerte til Hermitisk .


Generelle skalarprodukter i R n og i C n
Mer generelt, i det virkelige tilfellet, er hver symmetrisk og positivt bestemt matrise definert av


et skalarprodukt; på samme måte, i det komplekse tilfellet, for hver positivt bestemte hermitiske matrise, over


definerer et skalarprodukt. Her betegner vinkelparentene på høyre side standard skalarprodukt , vinkelparentesene med indeksen på venstre side angir skalarproduktet definert av matrisen .


Hvert skalarprodukt på eller kan representeres på denne måten av en positivt bestemt symmetrisk matrise (eller positivt bestemt hermitisk matrise).


L 2 skalarprodukt for funksjoner
På uendelig-dimensjonale vektorrommet av den kontinuerlige reelle verdier funksjoner i intervallet den -scalar produktet er via
![C ^ 0 ([a, b], \ R)](https://wikimedia.org/api/rest_v1/media/math/render/svg/9031f182bf36a2537c1747fe6a7f7ee2461b6bdb)
![[fra]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)


definert for alle .
![f, g \ i C ^ 0 ([a, b], \ R)](https://wikimedia.org/api/rest_v1/media/math/render/svg/97d766f23dd6e08b9abc30da269fabe6663e78e2)
For generaliseringer av dette eksemplet, se Prähilbertraum og Hilbertraum .
Frobenius dot-produkt for matriser
På matrise løpet av den virkelige - matriser er for ved




definerer et skalarprodukt. Tilsvarende, i rommet av komplekse matriser for av




definerer et skalarprodukt. Dette skalarproduktet kalles Frobenius-skalarproduktet og den tilhørende normen kalles Frobenius-normen .
Norm, vinkel og ortogonalitet
Lengden på en vektor i det euklidiske rommet tilsvarer generelt skalære produktrom til normen indusert av det skalære produktet . Denne normen defineres ved å overføre formelen for lengden fra det euklidiske rommet som roten til det skalære produktet til vektoren med seg selv:

Dette er mulig fordi det på grunn av den positive klarheten ikke er negativt. Trekantulikheten som kreves som et normaksiom følger av Cauchy-Schwarz-ulikheten

Er det, kan denne ulikheten også


bli omformet. Derfor kan man generelt også bruke reelle vektorrom

definere vinkelen på to vektorer. Vinkelen definert på denne måten er mellom 0 ° og 180 °, dvs. mellom 0 og Det er en rekke forskjellige definisjoner for vinkler mellom komplekse vektorer.

I det generelle tilfellet kalles vektorer som har det skalære produktet null, ortogonale:

Matrisevisning
Er et n-dimensjonalt vektorrom og en base av slike, hver prikk på med en ( ) - matrise , Gram-matrisen , er beskrevet i det skalære produktet. Oppføringene dine er de skalære produktene til basisvektorene:








-
 med for
med for

Det skalære produktet kan deretter representeres ved hjelp av grunnlaget: Har vektorene representasjonen
i forhold til grunnlaget

-
 og
og 
så i virkeligheten

Man betegner med koordinatvektorene

-
 og
og 
så det er sant

hvor matriksproduktet gir en matrise, dvs. et reelt tall. Med vilje rad vektoren betegnet ved transponering fra den kolonnevektor dannet.



I det komplekse tilfellet gjelder det samme

hvor overlinjen betegner kompleks konjugasjon og linjevektoren som skal ligge sammen .


Hvis det er en ortonormal basis , det vil si holder for alle og for alle, er da den identitetsmatrisen , og det holder







i virkeligheten og

i den komplekse saken. Når det gjelder en ortonormal basis, tilsvarer skalarproduktet av og dermed standard skalarproduktet til koordinatvektorene og / eller




Se også
litteratur
weblenker
-
Informasjon og materiale på skalarproduktet for det øvre nivået statlig utdanningsserver Baden-Württemberg
- Joachim Mohr: Introduksjon til skalarproduktet
- Video: prikkprodukt . Jörn Loviscach 2010, gjort tilgjengelig av Technical Information Library (TIB), doi : 10.5446 / 9742 .
- Video: prikkprodukt og vektorprodukt . Jörn Loviscach 2011, gjort tilgjengelig av Technical Information Library (TIB), doi : 10.5446 / 9929 .
- Video: prikkprodukt, del 1 . Jörn Loviscach 2011, gjort tilgjengelig av Technical Information Library (TIB), doi : 10.5446 / 10212 .
- Video: Punktprodukt del 2, ortogonalitet . Jörn Loviscach 2011, gjort tilgjengelig av Technical Information Library (TIB), doi : 10.5446 / 10213 .
- Video: Av vektorer og deres prikkprodukt - vektorberegning del 1 . Jakob Günter Lauth (SciFox) 2013, gjort tilgjengelig av Technical Information Library (TIB), doi : 10.5446 / 17886 .
Individuelle bevis
-
↑ Synonymt med:

-
^ Liesen, Mehrmann : Lineare Algebra . S. 168 .
-
^ Walter Rudin : Real and Complex Analysis . 2. forbedret utgave. Oldenbourg Wissenschaftsverlag, München 2009, ISBN 978-3-486-59186-6 , s. 91 .
-
^ Klaus Scharnhorst: Vinkler i komplekse vektorrom . I: Acta Applicandae Math. Volum 69 , 2001, s. 95-103 .
























































































































































![C ^ 0 ([a, b], \ R)](https://wikimedia.org/api/rest_v1/media/math/render/svg/9031f182bf36a2537c1747fe6a7f7ee2461b6bdb)
![[fra]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)


![f, g \ i C ^ 0 ([a, b], \ R)](https://wikimedia.org/api/rest_v1/media/math/render/svg/97d766f23dd6e08b9abc30da269fabe6663e78e2)












































