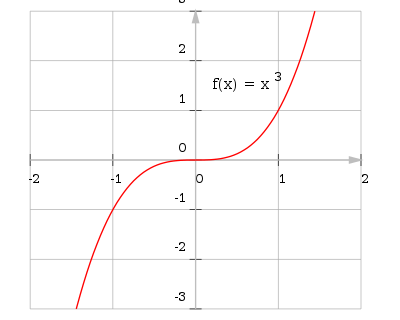
Kurvediskusjon

I matematikk, kurve diskusjon er forstått å være de undersøkelse av grafen til en funksjon for dens geometriske egenskaper, så som krysningene med koordinataksene, høye og lave punkter , vendepunkter , muligens sadel og flate punkter , asymptoter , oppførsel ved uendelig , etc. Denne informasjonen gjør det mulig å lage en skisse av grafen der alle disse egenskapene som er karakteristiske for funksjonen kan leses ut umiddelbart.

I dag er det imidlertid ikke lenger målet med en kurvediskusjon å støtte folk i å produsere en mest presis tegning av grafen til funksjonen: i mellomtiden er hver funksjonsplotter ( f.eks. En grafisk kalkulator , en smarttelefon med riktig programvare, et regneark program eller datamaskinalgebra Software ) bedre.

Snarere er målet med kurvediskusjonen

• nøyaktig bestemme koordinatene til de karakteristiske punktene i grafen (bare omtrentlige verdier kan leses fra et funksjonsplott);
• for å bevise karakteristiske egenskaper som symmetri eller atferd i uendelig . Fra en funksjonsplott kan man bare lese utsagn om den avbildede delen av koordinatsystemet, f.eks. Som for området , . Enten grafen til en funksjon men z. Hvis du for eksempel “dingler” igjen eller ikke, kan en pålitelig uttalelse bare komme på grunnlag av en kurvediskusjon.${\ displaystyle -6 \ leq x \ leq 6}$${\ displaystyle -4 \ leq y \ leq 10}$${\ displaystyle x = 10.000}$
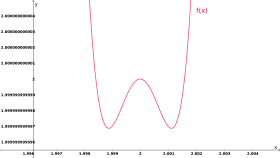
• se nærmere på : et tilsynelatende lokalt minimum kan vise seg å være et lokalt maksimum - gitt passende forstørrelse. Sammenlign for eksempel de to plottene i funksjonen

${\ displaystyle f (x) = 2 \ cdot (x-2) ^ {4} -0 {,} 000005 \ cdot (x-2) ^ {2} +2}$

i figur 1 eller figur 2. En kurvediskusjon avslører alltid slike fenomener, enten de foregår i det molekylære domenet eller i astronomiske dimensjoner: fordi en kurvediskusjon ikke - som et funksjonsplott - avhenger av oppløsningen.

I tillegg kan en kurve diskusjon også utføres på en svært lik måte for funksjoner som er avhengig av mange variabler (for eksempel på , og i stedet for bare ). En to- eller tredimensjonal visualisering av en slik funksjon er ikke lenger mulig. ${\ displaystyle x_ {1}}$${\ displaystyle x_ {2}}$${\ displaystyle x_ {3}}$${\ displaystyle x}$

Viktigheten av kurvediskusjonen blir også tydelig på bakgrunn av at i beslutningsstøttende systemer høye og lave punkter automatisk , dvs. H. uten brukerinteraksjon. Hvis man for eksempel skal undersøke effekten av endringen i en randtilstand på variabelen som skal optimaliseres , vil et slikt system vise eller grafisk visualisere den respektive ekstreme verdien, mens en verdi som beskriver grensetilstanden (f.eks. Nivået av en ressurs) er variert.

Definisjonens domene

Når vi diskuterer en kurve, antas settet av alle reelle tall nesten alltid som grunnleggende sett. Det maksimale domenet til en funksjon er settet med alle reelle tall som funksjonsverdien er definert for. Det maksimale definisjonsdomenet er det samme for helt rasjonelle funksjoner (polynomfunksjoner) . Når det gjelder brøk-rasjonelle funksjoner , tilhører alle reelle tall, med unntak av nollene til nevneren, det maksimale definisjonsdomenet. ${\ displaystyle \ mathbb {R}}$${\ displaystyle f}$${\ displaystyle x}$${\ displaystyle f (x)}$${\ displaystyle \ mathbb {R}}$

Eksempler:

• ${\ displaystyle f (x) = {\ frac {1} {x (x-3)}}; \ quad D = \ mathbb {R} \ setminus \ {0; 3 \}}$

Nevneren til brøkdelen kan ikke være 0. Derfor er verdiene 0 og 3 ekskludert. ${\ displaystyle x}$

• ${\ displaystyle f (x) = {\ sqrt {25-x ^ {2}}}; \ quad D = \ {x \ in \ mathbb {R} | -5 \ leq x \ leq 5 \} = [- 5; 5]}$

Radikanten, dvs. det aritmetiske uttrykket under kvadratroten , må være større enn eller lik 0. Denne betingelsen er oppfylt nøyaktig for tallene hvis beløp er mindre enn eller lik 5.

• ${\ displaystyle f (x) = \ ln (x + 4); \ quad D = \ {x \ in \ mathbb {R} | x> -4 \} = \ left] -4; \ infty \ right [}$

Den naturlige loggfunksjonen er bare definert for positive argumenter. Så må gjelde. ${\ displaystyle \ ln}$${\ displaystyle x> -4}$

Kryss med koordinataksene

For å finne nuller av en funksjon og således skjæringspunktene til funksjonsgrafen med aksen, den oppløsning sett av den blir ligning beregnes. Den nøyaktige prosedyren avhenger av hvilken funksjon som undersøkes. For eksempel, hvis funksjonen er gitt med en brøkdel , settes telleren til 0 for å oppnå nuller. ${\ displaystyle f}$${\ displaystyle x}$ ${\ displaystyle f (x) = 0}$${\ displaystyle f}$

For å bestemme skjæringspunktet til funksjonsgrafen med aksen, brukes 0 for verdien. Den y-aksen skjærings inngår da . ${\ displaystyle y}$${\ displaystyle x}$${\ displaystyle (0 | f (0))}$

Symmetriegenskaper

For å svare på spørsmålet om grafen til den gitte funksjonen på noen måte er symmetrisk , må flere saker vurderes.

Aksial symmetri i forhold til y- aksen

• Grafen til en funksjon er aksialt symmetrisk med hensyn til -aksien hvis og bare hvis følgende gjelder for alle verdier i domenet:${\ displaystyle f}$${\ displaystyle y}$${\ displaystyle x}$

${\ displaystyle f (-x) = f (x)}$

Når det gjelder helt rasjonelle funksjoner, betyr denne tilstanden at bare til og med eksponenter forekommer.

Punkt symmetri med hensyn til opprinnelse

• Grafen til en funksjon er punktsymmetrisk med hensyn til opprinnelsen hvis og bare hvis følgende gjelder for alle verdier i domenet:${\ displaystyle f}$${\ displaystyle x}$

${\ displaystyle f (-x) = - f (x)}$

Grafen til en helt rasjonell funksjon er punktsymmetrisk med hensyn til opprinnelsen hvis og bare hvis bare odde eksponenter forekommer.

Aksial symmetri i forhold til hvilken som helst akse

• Aksial symmetri i forhold til den rette linjen med ligningen (parallelt med -aksen) kan kontrolleres ved bruk av tilstanden${\ displaystyle x = x_ {0}}$${\ displaystyle y}$

${\ displaystyle f (x_ {0} -h) = f (x_ {0} + h).}$

Grafene til de kvadratiske funksjonene er blant annet aksialt symmetriske . I dette tilfellet resulterer symmetriaksen fra koordinaten til ( parabolen ) toppunktet. ${\ displaystyle x}$

Punkt symmetri med hensyn til et hvilket som helst senter

• Betingelsen for punktsymmetri med hensyn til poenget er${\ displaystyle (x_ {0} | y_ {0})}$

${\ displaystyle f (x_ {0} -h) + f (x_ {0} + h) = 2y_ {0}}$

eller tilsvarende)

${\ displaystyle f (x_ {0} + h) -y_ {0} = y_ {0} -f (x_ {0} -h).}$

Grafene til alle kubiske funksjoner er punktsymmetriske. Sentrum av symmetri er alltid (eneste) vendepunkt (se nedenfor).

Ekstreme poeng

Til de ekstreme punktene - det vil si høye og lave punkter - er en kontinuerlig differensierbar funksjon for å bestemme den første, derivat av sett lik 0, det vil si at løsningen av ligningen beregnes. Alle løsninger på denne ligningen er mulige såkalte ekstreme punkter . ${\ displaystyle f}$${\ displaystyle f}$${\ displaystyle f '\, (x) = 0}$

Imidlertid er tilstanden bare en nødvendig betingelse for ekstreme punkter. Et punkt med en skråning på 0 kan også være et sadelpunkt . Standardeksemplet er på punkt 0. Selv om punktet ikke er et ekstremt punkt, men et sadelpunkt. ${\ displaystyle f '\, (x) = 0}$${\ displaystyle f (x) = x ^ {3}}$${\ displaystyle f '\, (0) = 0}$${\ displaystyle (0 | 0)}$

En av tilstrekkelige betingelser nevnt nedenfor er derfor nødvendig for å bevise egenskapen til ekstreme punkter .

Nødvendig tilstand

Det er klart at tangenten til en funksjonsgraf må gå parallelt med aksen på et ekstremt punkt . Den helning av en slik tangent må derfor ha verdien 0. Følgende gjelder mer presist: ${\ displaystyle x}$

• ${\ displaystyle f}$være en reell funksjon, som er definert i et åpent intervall og som (med ) kan differensieres på det tidspunktet . Tar på punktet en relativ ekstrem (dvs. et relativt maksimum eller minimum), så sant .${\ displaystyle I}$${\ displaystyle x_ {0}}$${\ displaystyle x_ {0} \ i I}$${\ displaystyle f}$${\ displaystyle x_ {0}}$${\ displaystyle f '\, (x_ {0}) = 0}$

På kanten av definisjonsområdet og på steder der den gitte funksjonen ikke kan differensieres, oppfylles ikke kravene i denne tilstanden. Relative ekstremer på slike punkter kan vanligvis ikke bestemmes ved å sette derivatet til null.

Tilstrekkelig tilstand: verdien av det andre derivatet

Følgende tilstrekkelige tilstand gir ofte en praktisk måte å bevise en relativ extremum og samtidig bestemme typen (maksimum eller minimum). Siden det andre derivatet også kreves, blir det noen ganger referert til som -Test. ${\ displaystyle f ''}$

• ${\ displaystyle f}$være en reell funksjon som er definert i et åpent intervall og som kan differensieres to ganger.${\ displaystyle I}$

Gjelder ett sted samtidig ${\ displaystyle x_ {0} \ i I}$

1. ${\ displaystyle f '(x_ {0}) = 0}$ og
2. ${\ displaystyle f '' (x_ {0})> 0}$,

så har et relativt minimum på dette punktet. ${\ displaystyle f}$

Gjelder derimot samtidig

1. ${\ displaystyle f '(x_ {0}) = 0}$ og
2. ${\ displaystyle f '' (x_ {0}) <0}$,

så har et relativt maksimum på dette punktet. ${\ displaystyle f}$

Eksempel:

${\ displaystyle {\ begin {justert} f (x) & = - x ^ {2} + 8x \\ f '(x) & = - 2x + 8 \\ f' '(x) & = - 2 \ end {justert}}}$

Å sette det første derivatet ( ) til null gir . Å sette inn i det andre derivatet gir (betingelse for et relativt maksimum). Grafen for har nøyaktig ett ekstremt punkt, nemlig et høydepunkt med koordinat 4. ${\ displaystyle -2x + 8 = 0}$${\ displaystyle x = 4}$${\ displaystyle f '' (4) = - 2 <0}$${\ displaystyle f}$${\ displaystyle x}$

Noen ganger både og . I dette tilfellet er det behov for ytterligere undersøkelser for å avgjøre om det er et ekstremt punkt. Spesielt betyr dette at et derivat må lages til det er et derivat av jevn rekkefølge - fjerde, sjette, ... rekkefølge - som ikke er lik 0 på dette punktet. ${\ displaystyle f '(x_ {0}) = 0}$${\ displaystyle f '' (x_ {0}) = 0}$

Det enkleste eksemplet er . De tre første derivatene på punktet , det vil si og har hver verdi 0. Bare det fjerde derivatet muliggjør påvisning av ekstremum. Det positive tegnet viser at det er et relativt minimum på dette punktet . ${\ displaystyle f (x) = x ^ {4}}$${\ displaystyle x_ {0} = 0}$${\ displaystyle f '(0)}$${\ displaystyle f '' (0)}$${\ displaystyle f '' '(0)}$${\ displaystyle f ^ {(4)} (x) = 24}$${\ displaystyle f ^ {(4)} (0) = 24 \ neq 0}$${\ displaystyle x_ {0} = 0}$

I sjeldne tilfeller mislykkes også dette mer generelle kriteriet, nemlig når alle derivater på punktet er lik 0. ${\ displaystyle x_ {0}}$

Tilstrekkelig tilstand: tegn på det første derivatet

En annen metode for å verifisere ekstreme punktegenskapen krever ikke beregning av det andre derivatet. Det undersøkes om det første derivatet endrer tegnet på det aktuelle punktet . Denne fremgangsmåten, noen ganger referert til som den fortegnsendringen metode (VZW metode), kan klart tolkes som følger: ${\ displaystyle f '(x)}$${\ displaystyle x_ {0}}$

Hvis du går gjennom funksjonsgrafen i nærheten av et høyt punkt fra venstre til høyre, kan utseendet til denne kurven beskrives som følger:

1. Funksjonsgrafen stiger til venstre for høydepunktet. Skråningen er positiv.
2. På selve høydepunktet løper tangenten horisontalt. Skråningen er 0.
3. Funksjonsgrafen faller til høyre for høydepunktet. Skråningen er negativ.

Det samme gjelder lavt, bare omvendt.

• ${\ displaystyle f}$være en reell funksjon som er definert og differensierbar i et åpent intervall .${\ displaystyle I}$

Gjelder ett sted samtidig ${\ displaystyle x_ {0} \ i I}$

1. ${\ displaystyle f '(x_ {0}) = 0}$,
2. ${\ displaystyle f '(x) <0}$for og${\ displaystyle x <x_ {0}, \, x \ i I}$
3. ${\ displaystyle f '(x)> 0}$for ,${\ displaystyle x> x_ {0}, \, x \ i I}$

så har et relativt minimum på dette punktet. ${\ displaystyle f}$

Gjelder ett sted samtidig ${\ displaystyle x_ {0} \ i I}$

1. ${\ displaystyle f '(x_ {0}) = 0}$,
2. ${\ displaystyle f '(x)> 0}$for og${\ displaystyle x <x_ {0}, \, x \ i I}$
3. ${\ displaystyle f '(x) <0}$for ,${\ displaystyle x> x_ {0}, \, x \ i I}$

så har et relativt maksimum på dette punktet. ${\ displaystyle f}$

Eksempel:

${\ displaystyle f (x) = x ^ {4}}$

${\ displaystyle f '(x) = 4x ^ {3}}$

Å sette derivatet til null ( ) gir som et punkt med en horisontal tangens og dermed som en kandidat for et ekstremt punkt . I VZW-testen vurderes verdier som er mindre eller større enn 0. ${\ displaystyle 4x ^ {3} = 0}$${\ displaystyle x = 0}$${\ displaystyle x}$

${\ displaystyle f '(x) = 4x ^ {3} <0}$ til ${\ displaystyle x <0}$

${\ displaystyle f '(x) = 4x ^ {3}> 0}$ til ${\ displaystyle x> 0}$

viser at det er et lavpunkt.

Et problem med VZW-testen er at tegnet på derivatet ikke trenger å bestemmes for et enkelt siffer, men for et helt intervall. I skolematematikk bestemmer man derfor ofte bare tegnet for et enkelt siffer i intervallet og konkluderer ut fra dette at dette tegnet gjelder hele intervallet. Denne prosedyren er tillatt hvis funksjonen kontinuerlig kan differensieres i intervallet . ${\ displaystyle I}$

Historisk sidemerknad: Bestemmelsen av ytterpunktene fra den tangente skråningen ble først foreslått av Fermat i et brev til Descartes - før begrepet avledning eksisterte.

Vendepunkter

Vendepunkter er de punktene der den gitte funksjonsgrafen skifter mellom en venstre og en høyre kurve. Den type krumning kan bli gjenkjent - under visse forhold - fra fortegnet av den andre deriverte . Et positivt tegn indikerer en venstre krumning, et negativt tegn indikerer en høyre krumning. I standardprosedyren for å bestemme vendepunktene blir det andre derivatet derfor satt lik 0. Løsningene til ligningen (se nødvendig tilstand) kommer i tvil som vendepunkter . En av de tilstrekkelige forholdene som er oppført nedenfor, kan deretter brukes til å bevise at et vendepunkt faktisk har skjedd. ${\ displaystyle f '' (x)}$${\ displaystyle f '' (x) = 0}$

På bayerske yrkesfaglige videregående skoler er vendepunkter definert som ekstreme punkter i den første avledningen.

Nødvendig tilstand

• ${\ displaystyle f}$være en reell funksjon som er definert i et åpent intervall og kontinuerlig differensierbar to ganger. Gjør grafen på stedet for et vendepunkt, skal det${\ displaystyle I}$${\ displaystyle f}$${\ displaystyle x_ {0} \ i I}$

${\ displaystyle f '' (x_ {0}) = 0.}$

Tilstrekkelig tilstand: verdien av det tredje derivatet

Den sistnevnte tilstanden er ikke tilstrekkelig for videre undersøkelser. En tilstrekkelig tilstand som ofte brukes til å oppdage vendepunkter, er basert på det tredje derivatet:

• ${\ displaystyle f}$være en reell funksjon som er definert i et åpent intervall og tre ganger differensierbart. Gjelder ett sted samtidig${\ displaystyle I}$${\ displaystyle x_ {0} \ i I}$

1. ${\ displaystyle f '' (x_ {0}) = 0}$ og
2. ${\ displaystyle f '' '(x_ {0}) \ neq 0,}$

så har grafen for på det punktet et vendepunkt. ${\ displaystyle f}$${\ displaystyle x_ {0}}$

Tilstrekkelig tilstand: tegn på det andre derivatet

Hvis, i tillegg til det andre derivatet, det tredje derivatet også er 0 på dette punktet, mislykkes det sistnevnte kriteriet. I dette tilfellet undersøker man om tegnet på det andre derivatet endres. For dette formål velger man en verdi som er mindre og en større enn null til det andre derivatet (dvs. koordinaten til vendepunktet). Disse to verdiene settes inn i det andre derivatet. Hvis tegnene på verdiene til det andre derivatet er forskjellige på disse punktene, er det et vendepunkt. Hvis tegnet endres fra minus til pluss, er det et vendepunkt med overgang fra høyre til venstre kurve. Hvis tegnet endres fra pluss til minus, er det et vendepunkt med overgang fra venstre til høyre kurve. ${\ displaystyle x_ {0}}$${\ displaystyle x_ {0}}$${\ displaystyle x}$

• ${\ displaystyle f}$være en reell funksjon som er definert i det åpne intervallet og kan skilles to ganger. Gjelder samtidig${\ displaystyle I}$${\ displaystyle x_ {0} \ i I}$

1. ${\ displaystyle f '' (x_ {0}) = 0}$,
2. ${\ displaystyle f '' (x) <0}$for , og${\ displaystyle x <x_ {0}}$${\ displaystyle x \ i I}$
3. ${\ displaystyle f '' (x)> 0}$for ,${\ displaystyle x> x_ {0}}$${\ displaystyle x \ i I}$

eller samtidig

1. ${\ displaystyle f '' (x_ {0}) = 0}$,
2. ${\ displaystyle f '' (x)> 0}$for , og${\ displaystyle x <x_ {0}}$${\ displaystyle x \ i I}$
3. ${\ displaystyle f '' (x) <0}$for , ,${\ displaystyle x> x_ {0}}$${\ displaystyle x \ i I}$

så har grafen for på det punktet et vendepunkt. ${\ displaystyle f}$${\ displaystyle x_ {0}}$

Spesielt tilfelle: sadelpunkter

Et vendepunkt med en horisontal tangens kalles et sadelpunkt eller et terrassepunkt. For ham, og som i eksemplet med funksjonen med ligningen, gjelder${\ displaystyle f '(x) = 0}$${\ displaystyle f '' (x) = 0}$

${\ displaystyle f (x) = {x ^ {3}}}$

på det punktet . ${\ displaystyle x = 0}$

Dette er imidlertid ikke et tilstrekkelig kriterium, det kan og vil være uten at et sadelpunkt oppstår, som vist i følgende eksempel: ${\ displaystyle f '(x) = 0}$${\ displaystyle f '' (x) = 0}$

${\ displaystyle f (x) = {x ^ {4}}}$

Et sadelpunkt er bare bevist når det er; Mer generelt gjelder følgende: Det er et vendepunkt hvis graden av det første derivatet annet enn 0 er merkelig; hvis graden er jevn, er den ekstrem. I tilfeller som ${\ displaystyle f '' '\ neq 0}$

${\ displaystyle f (x) = {x ^ {5}}}$

Imidlertid er det tredje derivatet ubrukelig, siden det også forsvinner i 0-posisjonen. Skiltendringskriteriet hjelper her.

Poler

I brøk-rasjonelle funksjoner er en pol til stede ved et punkt hvis nevnerpolynomet har null ved og tellerpolynomet har null av lavere orden på eller ingen null ved . ${\ displaystyle p}$${\ displaystyle p}$${\ displaystyle p}$${\ displaystyle p}$

Hvis både telleren og nevnerpolynomet har null og rekkefølgen på null i tellerpolynomet ikke er mindre enn det til nevnerpolynomet, er det et kontinuerlig eliminerbart definisjonsgap . ${\ displaystyle p}$

I universitetsmatematikk er det andre typer udefinerte stillinger som verken er flyttbare hull eller polposisjoner.

mellomrom

Når det gjelder brøk-rasjonelle funksjoner, er det et kontinuerlig korrigerbart definisjonsgap på ett punkt hvis ikke bare et null av nevneren, men også et null av telleren er av minst samme grad. I dette tilfellet kan den tilknyttede lineære faktoren forkortes. ${\ displaystyle x_ {0}}$${\ displaystyle x_ {0}}$${\ displaystyle (x-x_ {0})}$

Eksempel: har et definerbart gap i definisjonen på dette punktet . Ved å redusere faktoren får du: ${\ displaystyle {\ tfrac {x ^ {2} -4} {x-2}}}$${\ displaystyle x = 2}$${\ displaystyle (x-2)}$

${\ displaystyle {\ frac {x ^ {2} -4} {x-2}} = {\ frac {(x + 2) \ cdot (x-2)} {x-2}} = x + 2}$   (for ).${\ displaystyle x \ neq 2}$

En annen måte å teste om det er et kontinuerlig korrigerbart definisjonsgap er å beregne grenseverdien . Hvis denne grensen eksisterer og er endelig, er det et løpende løseløst gap. ${\ displaystyle x_ {0}}$${\ displaystyle \ lim _ {x \ rightarrow x_ {0}} f (x)}$

Oppførsel i uendelig

For å finne ut atferd ved uendelig, blir funksjonsverdien til funksjonen undersøkt når den øker utover alle grenser, dvs. den går imot : ${\ displaystyle f (x)}$${\ displaystyle x}$${\ displaystyle \ infty}$

${\ displaystyle \ lim _ {x \ to \ infty} f (x) \ ;;}$

Det samme for . ${\ displaystyle - \ infty}$

Oversikt over kriterier

Drøftes ${\ displaystyle f \ colon x \ mapsto f (x)}$
Undersøkelsesaspekt	kriterier
Null	${\ displaystyle f (x_ {N}) = 0 \,}$
Ekstremt poeng	${\ displaystyle f '(x_ {E}) = 0 \,}$	(nødvendig kriterium)
	${\ displaystyle f '(x_ {E}) = 0 \ land f' '(x_ {E}) \ neq 0}$	(tilstrekkelig kriterium)
Minimum stilling	${\ displaystyle f '(x_ {E}) = 0 \,}$	(nødvendig kriterium)
	${\ displaystyle f '(x_ {E}) = 0 \ land f' '(x_ {E})> 0}$	(tilstrekkelig kriterium)
Maksimal posisjon	${\ displaystyle f '(x_ {E}) = 0 \,}$	(nødvendig kriterium)
	${\ displaystyle f '(x_ {E}) = 0 \ land f' '(x_ {E}) <0}$	(tilstrekkelig kriterium)
Vendepunkt	${\ displaystyle f '' (x_ {W}) = 0 \,}$	(nødvendig kriterium)
	${\ displaystyle f '' (x_ {W}) = 0 \ land f '' '(x_ {W}) \ neq 0}$	(tilstrekkelig kriterium)
Seteposisjon	${\ displaystyle f '(x_ {W}) = 0 \ land f' '(x_ {W}) = 0}$	(nødvendig kriterium)
	${\ displaystyle f '(x_ {W}) = 0 \ land f' '(x_ {W}) = 0 \ land f' '' (x_ {W}) \ neq 0}$	(tilstrekkelig kriterium)
Oppførsel i uendelig	${\ displaystyle \ lim _ {x \ to \ infty} f (x)}$,	${\ displaystyle \ lim _ {x \ to - \ infty} f (x)}$
symmetri
Aksesymmetri til koordinataksen	${\ displaystyle f (x) = f (-x) \,}$
Punkt symmetri til opprinnelsen til koordinatene	${\ displaystyle -f (x) = f (-x) \,}$
monotoni
økende / strengt økende	${\ displaystyle f '(x) \ geq 0}$	${\ displaystyle f '(x)> 0 \,}$
fallende / strengt fallende	${\ displaystyle f '(x) \ leq 0}$	${\ displaystyle \, f '(x) <0}$
krumning
Venstre kurve / konveks bue (åpen øverst)	${\ displaystyle f '' (x)> 0 \,}$
Høyre kurve / konkave bue (åpen nederst)	${\ displaystyle f '' (x) <0 \,}$
periodisitet	${\ displaystyle f (x + p) = f (x) \,}$
Drøftes ${\ displaystyle f \ colon x \ mapsto {\ frac {p (x)} {q (x)}}}$
Undersøkelsesaspekt	kriterier
Definisjonens domene	${\ displaystyle \ mathbb {D} = \ mathbb {R} \ setminus \ lbrace x_ {0} \ mid q (x_ {0}) = 0 \ rbrace}$
Polestilling	${\ displaystyle q (x_ {p}) = 0 \,}$	(nødvendig kriterium)
	${\ displaystyle q (x_ {p}) = 0 \ land p (x_ {p}) \ neq 0}$	(tilstrekkelig kriterium)

Eksempel: en helt rasjonell funksjon

Funksjonen som skal undersøkes er:

${\ displaystyle f (x) = 3x ^ {3} -5x ^ {2} +8}$

Grafen til funksjonen er vist i svart på bildet, og de første (røde) og andre (blå) derivatene vises: ${\ displaystyle f}$

nullpunkt

Nullet kan bli funnet ved prøving og feiling (for eksempel ved å lage en verditabell ) eller i henhold til den gaussiske slutningen om at hvert heltall null må være en skillelinje for det absolutte begrepet 8 . Hvis det ikke var noe like lett gjenkjennelig null, kunne Cardanos formel brukes til ligninger av 3. grad eller Newtons tilnærmingsmetode . ${\ displaystyle x = -1}$

Den lineære faktoren tilhører null . For å finne de andre nullene utføres en polynomdeling ved hjelp av denne lineære faktoren, og resultatet settes lik 0. Resultatet oppnås litt raskere med Horner-ordningen . På denne måten reduseres ligningsgraden med 1. ${\ displaystyle x = -1}$${\ displaystyle (x - (- 1)) = (x + 1)}$

${\ displaystyle (3x ^ {3} -5x ^ {2} +8) :( x + 1) = 3x ^ {2} -8x + 8}$

Den nye ligningen har ingen løsning. er følgelig det eneste virkelige null. ${\ displaystyle 3x ^ {2} -8x + 8 = 0}$${\ displaystyle x = -1}$

Ekstreme poeng

Den første avledede funksjonen er

${\ displaystyle f '(x) = 9x ^ {2} -10x = 9x (x - {\ tfrac {10} {9}}) \,}$.

Dette har nuller på og ved . Dette betyr at det kan være ekstreme punkter her. ${\ displaystyle x_ {1} = 0}$${\ displaystyle x_ {2} = {\ tfrac {10} {9}}}$

Den andre avledede funksjonen

${\ displaystyle f '' (x) = 18x-10 \,}$

har funksjonsverdiene ovennevnte steder

${\ displaystyle f '' (x_ {1}) = 18 \ cdot 0-10 = -10 <0}$

eller.

${\ displaystyle f '' (x_ {2}) = 18 \ cdot {\ tfrac {10} {9}} - 10 = 10> 0.}$

Derfor har funksjonsgrafen et høyt punkt (første derivat lik 0, andre derivat negativt) og et lavt punkt (første derivat lik 0, andre derivat positivt). De koordinatene til de to ytterpunkter blir oppnådd ved å sette inn koordinatene i . ${\ displaystyle x_ {1}}$${\ displaystyle x_ {2}}$${\ displaystyle y}$${\ displaystyle x}$${\ displaystyle f (x)}$

${\ displaystyle {\ begin {align} y_ {1} & = f (0) = 3 \ cdot 0 ^ {3} -5 \ cdot 0 ^ {2} + 8 = 8 \\ y_ {2} & = f ({\ tfrac {10} {9}}) = 3 \ cdot \ left ({\ tfrac {10} {9}} \ right) ^ {3} -5 \ cdot \ left ({\ tfrac {10} { 9}} \ høyre) ^ {2} + 8 = 5 {\ tfrac {229} {243}} \ ende {justert}}}$

Høyt punkt: ${\ displaystyle (0 | 8)}$

Lavt punkt: ${\ displaystyle ({\ tfrac {10} {9}} | 5 {\ tfrac {229} {243}})}$

Vendepunkter

For å bestemme vendepunktene settes det andre derivatet lik null: ${\ displaystyle f '' (x) = 18x-10}$

${\ displaystyle 18x-10 = 0}$

Den eneste løsningen på denne ligningen er . Det tredje derivatet kan brukes til å bekrefte at det virkelig er et vendepunkt . På grunn av ${\ displaystyle x_ {3} = {\ tfrac {5} {9}}}$${\ displaystyle f '' '(x) = 18}$

${\ displaystyle f '' '(x_ {3}) = f' '' ({\ tfrac {5} {9}}) = 18 \ neq 0}$

vendepunktet er sikret. Den koordinaten til vendepunktet medfører ${\ displaystyle y}$

${\ displaystyle y_ {3} = f (x_ {3}) = 3 \ cdot \ left ({\ tfrac {5} {9}} \ right) ^ {3} -5 \ cdot \ left ({\ tfrac { 5} {9}} \ right) ^ {2} + 8 = 6 {\ tfrac {236} {243}}.}$

Vendepunkt: ${\ displaystyle ({\ tfrac {5} {9}} | 6 {\ tfrac {236} {243}})}$

Polakker og oppførsel i uendelig

Det er ingen polynomer i polynomer. Som et polynom av ulik rekkefølge (høyeste eksponent kl ) går funksjonen mot eller , hvis den er mot eller går. ${\ displaystyle x ^ {3}}$${\ displaystyle + \ infty}$${\ displaystyle - \ infty}$${\ displaystyle x}$${\ displaystyle + \ infty}$${\ displaystyle - \ infty}$

Eksempel: fraksjonell rasjonell funksjon

Funksjonen er gitt av ligningen

${\ displaystyle {f (x)} = {\ frac {x ^ {3} -4x ^ {2} + 4x} {4x ^ {2} -8x + 4}}}$

Definisjonens domene

Funksjonen er bare definert der nevneren ikke er lik 0. Å undersøke nevneren for nuller gir:

${\ displaystyle 4x ^ {2} -8x + 4 = 0}$

${\ displaystyle x ^ {2} -2x + 1 = 0}$

${\ displaystyle x = 1 + {\ sqrt {1-1}} = 1}$ eller ${\ displaystyle x = 1 - {\ sqrt {1-1}} = 1}$

Den kvadratiske ligningen har en dobbel løsning ved . Nevneren blir bare 0. Definisjonsområdet er følgelig ${\ displaystyle x = 1}$${\ displaystyle x = 1}$

${\ displaystyle \ mathbb {D} = \ mathbb {R} \ setminus \ {1 \},}$

settet med reelle tall, med unntak av 1. Nevneren kan - fordelt på lineære faktorer - som

${\ displaystyle 4 (x-1) (x-1)}$ eller ${\ displaystyle 4 (x-1) ^ {2}}$

skal skrives.

nullpunkt

Betingelsen for nuller er . For dette er det tilstrekkelig at telleren blir 0 så lenge nevneren ikke også blir 0. Undersøkelse av telleren for nuller viser: ${\ displaystyle f (x_ {N}) = 0 \,}$

${\ displaystyle x ^ {3} -4x ^ {2} + 4x = 0}$

${\ displaystyle x (x ^ {2} -4x + 4) = 0}$

${\ displaystyle x = 0}$eller eller${\ displaystyle x = 2 + {\ sqrt {4-4}} = 2}$${\ displaystyle x = 2 - {\ sqrt {4-4}} = 2}$

Telleren har et enkelt null ved og et dobbelt ved . Begge steder er innenfor definisjonsområdet. så har nuller i tillegg . ${\ displaystyle x = 0}$${\ displaystyle x = 2}$${\ displaystyle f (x)}$${\ displaystyle x_ {1} = 0}$${\ displaystyle x_ {2} = x_ {3} = 2}$

Telleren kan - fordelt på lineære faktorer - som

${\ displaystyle x (x-2) (x-2) = x (x-2) ^ {2}}$

skal skrives.

Som en del av skolen regnes matematikk ofte som viktig at i hver av indeksene for "null" skal skrives . ${\ displaystyle x}$${\ displaystyle N}$${\ displaystyle x_ {N} \,}$

Poler

På dette punktet har nevneren to nuller uten at telleren blir 0 samtidig. Så det er en stang ved . Hvis telleren også skal være 0, må rekkefølgen på nevneren null for en pol være større enn rekkefølgen på telleren null. ${\ displaystyle x = 1}$${\ displaystyle x = 1}$

Hvis nevneren til en brøk-rasjonell funksjon er lik 0 på ett punkt , er ikke funksjonen definert på dette punktet. Hvis nevneren er lik 0, men telleren ikke er lik 0, har funksjonen en pol på dette punktet ("uendelig punkt"). ${\ displaystyle x = a}$

symmetri

Grafen til funksjonen blir undersøkt for symmetri på dette punktet. Ofte er det bare en undersøkelse for aksesymmetri til -aksien (tilstand ) og for punktsymmetri til opprinnelsen til koordinatsystemet (tilstand ). ${\ displaystyle y}$${\ displaystyle f (-x) = f (x)}$${\ displaystyle f (-x) = - f (x)}$

I eksemplet, i

${\ displaystyle {f (x)} = {{x ^ {3} -4x ^ {2} + 4x} \ over {4x ^ {2} -8x + 4}}}$

${\ displaystyle x}$erstattet av . Etter å ha multiplisert er resultatet ${\ displaystyle -x}$

${\ displaystyle {f (-x)} = {{(- x) ^ {3} -4 (-x) ^ {2} +4 (-x)} \ over {4 (-x) ^ {2} -8 (-x) +4}} = {{- x ^ {3} -4x ^ {2} -4x} \ over {4x ^ {2} + 8x + 4}}}$.

Siden verken med eller med tilsvarer, er grafen verken aksialt symmetrisk til -aksen eller punkt symmetrisk til opprinnelsen. ${\ displaystyle f (-x)}$${\ displaystyle f (x)}$${\ displaystyle -f (x)}$${\ displaystyle f}$${\ displaystyle y}$

Undersøkelsen av aksesymmetri med hensyn til en hvilken som helst akse eller punktsymmetri med hensyn til et hvilket som helst punkt er noe vanskeligere. Aksial symmetri kan ekskluderes på grunn av og . På det meste ville skjæringspunktet til asymptotene (se nedenfor), dvs. punktet, komme i tvil som sentrum for symmetri (punktsymmetri) . Men siden for eksempel punktene og ikke er symmetriske med hensyn til hverandre , er heller ikke grafen punktsymmetrisk. ${\ displaystyle \ textstyle \ lim _ {x \ to - \ infty} f (x) = - \ infty}$${\ displaystyle \ textstyle \ lim _ {x \ to \ infty} f (x) = + \ infty}$${\ displaystyle (1 | - {\ tfrac {1} {4}})}$${\ displaystyle (0 | 0)}$${\ displaystyle (2 | 0)}$${\ displaystyle (1 | - {\ tfrac {1} {4}})}$

Derivater

Derivatene av

${\ displaystyle {f (x)} = {{x (x-2) ^ {2}} \ over {4 (x-1) ^ {2}}}.}$

Representasjonen i lineære faktorer er mer nyttig da det forenkler utregning og forkortelse. Først av alt resulterer dette

${\ displaystyle {\ begin {align} {f '(x)} & = {{(2x (x-2) + (x-2) ^ {2}) 4 (x-1) ^ {2} -x (x-2) ^ {2} \ cdot 8 (x-1)} \ over {16 (x-1) ^ {4}}} \\ & = {{(2x (x-2) + (x- 2) ^ {2}) (x-1) -2x (x-2) ^ {2}} \ over {4 (x-1) ^ {3}}} \\ & = {{(x-2) ((2x + (x-2)) (x-1) -2x (x-2))} \ over {4 (x-1) ^ {3}}} \\ & = {{(x-2) ((3x-2) (x-1) -2x (x-2))} \ over {4 (x-1) ^ {3}}} \\ & = {{(x-2) (3x ^ { 2} -3x-2x + 2-2x ^ {2} + 4x)} \ over {4 (x-1) ^ {3}}} \\ & = {{(x-2) (x ^ {2} - x + 2)} \ over {4 (x-1) ^ {3}}} \ slutt {justert}}}$

for det første derivatet. Så den andre

${\ displaystyle {\ begin {align} {f '' (x)} & = {{((x-2) (2x-1) + (x ^ {2} -x + 2)) (x-1) ^ {3} - (x-2) (x ^ {2} -x + 2) \ cdot 3 (x-1) ^ {2}} \ over {4 (x-1) ^ {6}}} \ \ & = {{((x-2) (2x-1) + (x ^ {2} -x + 2)) (x-1) -3 (x-2) (x ^ {2} -x + 2)} \ over {4 (x-1) ^ {4}}} \\ & = {{(2x ^ {2} -x-4x + 2 + x ^ {2} -x + 2) (x- 1) - (3x-6) (x ^ {2} -x + 2)} \ over {4 (x-1) ^ {4}}} \\ & = {{(3x ^ {2} -6x + 4) (x-1) - (3x ^ {3} -3x ^ {2} + 6x-6x ^ {2} + 6x-12)} \ over {4 (x-1) ^ {4}}} \ \ & = {{3x ^ {3} -3x ^ {2} -6x ^ {2} + 6x + 4x-4-3x ^ {3} + 3x ^ {2} -6x + 6x ^ {2} -6x +12} \ over {4 (x-1) ^ {4}}} \\ & = {{- 2x + 8} \ over {4 (x-1) ^ {4}}} \\ & = {{ 4-x} \ over {2 (x-1) ^ {4}}} \ end {justert}}}$

og det tredje derivatet

${\ displaystyle {\ begin {align} {f '' '(x)} & = {- {(x-1) ^ {4} - (4-x) 4 (x-1) ^ {3}} \ over {2 (x-1) ^ {8}}} \\ & = {- {(x-1) -4 (4-x)} \ over {2 (x-1) ^ {5}}} \ \ & = {- {x + 1-16 + 4x} \ over {2 (x-1) ^ {5}}} \\ & = {{3x-15} \ over {2 (x-1) ^ { 5}}} \ end {align}}}$

utdannet.

Ekstreme poeng

For dette må være. Det er nok å undersøke tellerens nuller: ${\ displaystyle f '(x) = 0 \,}$

${\ displaystyle {(x-2) (x ^ {2} -x + 2)} = 0 \,}$

har løsningen . Den andre braketten har ingen reelle løsninger. er innenfor definisjonsområdet. Funksjonsverdien på dette punktet er fordi det er null her. Det andre derivatet er på dette punktet , så det er et lavt punkt ved (2/0) . ${\ displaystyle x = 2}$${\ displaystyle x = 2}$${\ displaystyle f (2) = 0 \,}$${\ displaystyle f '' (2) = 1> 0 \,}$

Vendepunkter

Vendepunktet bestemmes ved å sette det andre derivatet lik 0. Fra denne tilnærmingen følger . Å erstatte denne verdien i det tredje derivatet gir . Så det er virkelig et vendepunkt. Beregningen av endelig resulterer i koordinaten . Vendepunktet vi ser etter er dermed . ${\ displaystyle x_ {W} = 4}$${\ displaystyle f '' '(4) = - {\ tfrac {1} {162}} \ neq 0}$${\ displaystyle f (4)}$${\ displaystyle y}$${\ displaystyle y_ {W} = {\ tfrac {4} {9}}}$${\ displaystyle (4 | {\ tfrac {4} {9}})}$

Asymptoter

På polen, det vil si på , er det en vertikal asymptote . Siden graden av telleren (3) til 1 er større enn for nevneren (2), for å gå opp . Forskjellen indikerer at grafen vil asymptotisk nærme seg en lineær funksjon (rett linje). Linjelinjen følger med polynomisk inndeling : ${\ displaystyle x = 1}$${\ displaystyle f (x)}$${\ displaystyle \ infty}$${\ displaystyle x}$${\ displaystyle \ infty}$${\ displaystyle 3-2 = 1}$

${\ displaystyle (x ^ {3} -4x ^ {2} + 4x) :( 4x ^ {2} -8x + 4) = {{1 \ over 4} x- {1 \ over 2} + {{- 1x + 2} \ over {4x ^ {2} -8x + 4}}}}$

For mot nærmer den siste termen 0. Ligningen til asymptoten er altså ${\ displaystyle x}$${\ displaystyle \ infty}$

${\ displaystyle {a (x)} = {{1 \ over 4} x- {1 \ over 2}}}$

Som regel:

• Hvis nevnergraden er større enn tellergraden, er asymptoten -aksien.${\ displaystyle x}$
• Hvis nevnergraden er den samme som tellergraden, er asymptoten parallell med -aksen.${\ displaystyle x}$
• Hvis nevnergraden er 1 mindre enn tellergraden, er asymptoten skjev.
• Hvis nevnergraden er mer enn 1 mindre enn tellergraden, er asymptoten ikke en rett linje, men buet. (Asymptotisk tilnærmingskurve)

Didaktiske spørsmål

I matematikkdidaktikk har det siden senest 1990-tallet blitt diskutert i hvilken grad kurvediskusjonen har blitt forbigått av tilgjengeligheten av grafiske lommeregner og dedikert programvare ( funksjonsplottere ).

Det kritiseres at kurvediskusjonen er en ren beregningsrutine som gir liten forståelse. På den annen side er det nettopp av den grunn at det er relativt populært blant svakere elever og studenter som eksamensfag å være forberedt relativt trygt.

I de sentrale Abitur-eksamenene har det derfor blitt fastslått at slike skjematiske oppgaver bare svært sjelden blir gitt. Mer populært er påkledde oppgaver eller oppgaver der det spørres om kontekstuell kunnskap, for eksempel om forholdet mellom avledningsfunksjonen og utgangsfunksjonen.

En didaktisk metode er beskrevet i områdeklassifisering .

litteratur

• Harald Scheid , Wolfgang Schwarz: Elementer av lineær algebra og analyse . Springer, 2009, ISBN 978-3-8274-2255-2 , s. 316-322.
• Harro Heuser : Lærebok for analyse. Del 1. Vieweg + Teubner, Wiesbaden 1980, ISBN 3-519-02221-4 , s. 293-295.
• Curve diskusjon i: Schülerduden - Matematikk II . Bibliographisches Institut & FA Brockhaus, 2004, ISBN 3-411-04275-3 , s. 235–241.
• Matematikk - Analyse . Cornelsen, 2002, ISBN 978-3-464-57216-0 , s. 108-142.

weblenker

• Forståelig tekst for kurvediskusjonen
• Eksemplariske kurvediskusjoner
• Nettkalkulator for kurvediskusjon med beregningsbane

Individuelle bevis

1. ↑ Friedrich Barth et al. (Red.): Matematiske formler og definisjoner . S. 64
2. ↑ Steffen Hahn, Susanne Prediger: Presentasjonsorientert kurvediskusjon - En bønn for det kvalitative (PDF; 306 kB) Universitetet i Bremen, på mathematik.uni-dortmund.de (arkivert)