Periodisk bane

Bevegelsen til en harmonisk oscillator resulterer i en periodisk bane i faseområdet .

Banen til en planet er ikke akkurat periodisk på grunn av apsisens rotasjon , animasjonen overdriver denne effekten veldig mye.

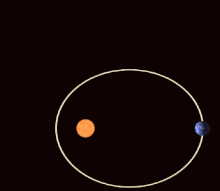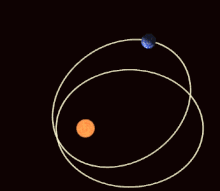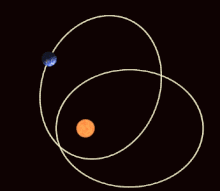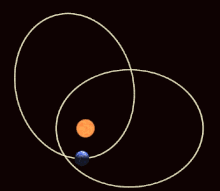
I den matematiske teorien om dynamiske systemer er en periodisk bane eller en periodisk bane (også: lukket bane ) en bevegelsesbane som alltid går tilbake til utgangspunktet etter en viss tidsperiode (" perioden "), som derfor er lukket i seg selv og dermed tilsvarer man repeterende, periodisk bevegelse. Poeng på periodiske baner kalles periodiske punkter .

Eksempler på periodiske baner er bevegelsen til en harmonisk oscillator eller planetbanene (som imidlertid ikke lenger er nøyaktig periodiske hvis man tar hensyn til apsisens rotasjon ).

definisjon

I et kontinuerlig dynamisk system, i. H. med : ${\ displaystyle t \ in \ mathbb {R}}$

${\ displaystyle \ varphi \ colon X \ times \ mathbb {R} \ to X}$

en flyt på et statsrom . den bane${\ displaystyle X}$

${\ displaystyle {\ mathcal {O}} (x, \ varphi): = \ left \ {\ varphi (x, t) | t \ in \ mathbb {R} \ right \}}$

av et punkt kalles en periodisk bane hvis det er en slik som ${\ displaystyle x \ i X}$${\ displaystyle T> 0}$

${\ displaystyle \ varphi (x, t + T) = \ varphi (x, t)}$

gjelder alle . Det minste mulige slike positive tallet kalles bane- perioden . ${\ displaystyle t \ in \ mathbb {R}}$${\ displaystyle T}$

Den samme definisjonen brukes for diskrete dynamiske systemer, her da, og er hele tall . ${\ displaystyle t}$${\ displaystyle T> 0}$

Periodiske baner av kronologisk kontinuerlige systemer har topologien til en sirkel, mens de i diskrete systemer (iterert kartlegging) består av et antall punkter som tilsvarer perioden, som er kartlagt på hverandre syklisk.

Seifert antagelse

Spørsmålet om strømningene av alle kontinuerlige vektorfelt på den tredimensjonale sfæren har en periodisk bane ble kjent som Seifert-formodningen . Det er moteksempler på denne antagelsen, selv med vilkårlig sterke betingelser for vektorfeltets differensierbarhet.

Reeb går i bane

Moteksemplene til Seifert-antagelsen viser at vektorfelt på den tredimensjonale sfæren kan ha veldig patologisk dynamikk. Man har en mer vanlig virkemåte for såkalte Reeb vektorfelt av standard kontaktkonstruksjonen på 3-sfære. For disse kan det påvises at det er alltid periodiske baner (såkalte Reeb orbites ) og metoder (f.eks kontakt homologi ) for å telle de periodiske orbites er tilgjengelige.

weblenker

• Periodisk bane (Scholarpedia)

Individuelle bevis

1. ↑ Fysikkens leksikon. Spectrum Academic Publishing House, Heidelberg 1998.
2. ↑ Artikkel med moteksempler:
   • V. Ginzburg, B. Gürel: A- glatt counterexample til Hamilton Seifert formodning i ]. ${\ displaystyle C ^ {2}}$${\ displaystyle R ^ {4}}$I: Ann. of Math. (2) 158, nr. 3, 2003, s. 953-976.
   • J. Harrison: Moteksempler til Seifert-antagelsen. I: Topologi. 27, nr. 3, 1988, s. 249-278.${\ displaystyle C ^ {2}}$
   • G. Kuperberg: Et volumbevarende moteksempel til Seifert-antagelsen. I: Kommentar. Math. Helv. 71, nr. 1, 1996, s. 70-97.
   • K. Kuperberg: Et jevnt moteksempel til Seifert-antagelsen. I: Ann. of Math. (2) 140, nr. 3, 1994, s. 723-732.
   • G. Kuperberg, K. Kuperberg: Generaliserte moteksempler til Seifert-antagelsen . I: Ann. of Math. (2) 143, nr. 3, 1996, s. 547-576.
   • H. Seifert: Lukkede integrerte kurver i 3-rom og isotopiske todimensjonale deformasjoner. I: Proc. Amer. Matematikk Soc. 1, 1950, s. 287-302.
   • PA Schweitzer: Moteksempler til Seifert-antagelsen og åpning av lukkede blader av foliering. I: Ann. of Math. (2) 100, 1974, s. 386-400.