Faseplass

Den faserommet beskriver settet av alle mulige tilstander av et dynamisk system . En tilstand er tydelig representert av et punkt i faseområdet. I mekanikk består den av generaliserte koordinater ( konfigurasjonsplass ) og tilhørende generaliserte hastigheter (se prinsippet om virtuell kraft ).

Bulk

Når det gjelder frihetsgrader (antall generaliserte koordinater eller romlige koordinater), er faseplassen -dimensjonal. For eksempel har en gasspartikkel frihetsgrader i tredimensjonalt rom , med tilhørende pulser er disse faseromskoordinater. Et system (gass) av partikler har et dimensjonalt faseplass. Imidlertid blir faseplasser i andre applikasjoner utenfor mekanikken også undersøkt. ${\ displaystyle n}$ ${\ displaystyle 2n}$${\ displaystyle n = 3}$${\ displaystyle 6}$${\ displaystyle N}$${\ displaystyle 6N}$

Den tidsmessige utviklingen av et punkt i faseområdet er beskrevet av differensiallikninger og representert av baner (baner, bane) i fasearealet. Dette er differensiallikninger av første orden i tid og er tydelig definert av et utgangspunkt (hvis differensiallikningen er uavhengig av tid, er dette autonome differensiallikninger ). Følgelig krysser ikke to baner heller i faseområdet, siden den videre forløpet ikke er entydig ved et kryssingspunkt. Lukkede kurver beskriver oscillerende (periodiske) systemer.

Konstruksjon av et fase (rom) portrett for en matematisk pendel

For systemer med opptil tre variabler kan faseplassen være representert grafisk. Spesielt for to variabler kan bevegelsen (baner, faseflytstrøm som et vektorfelt ) være tydelig representert i et faseplassportrett eller faseportrett og analysert kvalitativt ( faseplassanalyse, null linjer og faste punkter ).

Den historiske opprinnelsen til bruken av faseplasser spores ofte tilbake til Joseph Liouville - på grunn av Liouvilles teorem (1838) at i konservative systemer (med energibesparelse) er faseplassvolumet til nærliggende baner konstant over tid. Liouville hadde imidlertid ikke noe mekanisk system i tankene, men beviste setningen for generelle, vanlige differensiallikninger av første orden. Forbindelsen til mekanikk ble først foreslått av Carl Gustav Jacobi . Faseplassbegrepet dukket først opp etter at matematikere begynte å se på høyere dimensjonale rom i løpet av 1800-tallet. Den første bruken av faseplass i dagens forstand var av Ludwig Boltzmann i 1872 som en del av hans undersøkelser av statistisk mekanikk , som ble vedtatt av James Clerk Maxwell i 1879 . Konseptet ble deretter brukt i forelesningene av Boltzmann og Josiah Willard Gibbs om statistisk mekanikk, i artikkelen om statistisk mekanikk i Encyclopedia of Mathematical Sciences fra 1911 av Paul Ehrenfest og Tatjana Ehrenfest (som introduserte begrepet faseområde) og i kvalitativ teori om differensiallikninger av Henri Poincaré . ${\ displaystyle \ Gamma}$

Et dynamisk system, hvis baner fyller hele fasarommet, dvs. kommer så nært som ønsket til et hvilket som helst punkt i faseområdet, kalles ergodisk , se også ergodisk hypotese . I konservative mekaniske systemer (lukkede systemer), ifølge Liouvilles teorem, er faseplassvolumet til nabobaner konstant over tid, i dissipative systemer avtar det (åpne systemer).

I Hamiltonias mekanikk er faseplassen et eksempel på en symplektisk geometri, og ifølge Vladimir Arnold er Hamiltonian mekanikk geometrien i faseplassen . Siden impulsene er definert som derivater av Hamilton-funksjonen i henhold til de generelle koordinatene, er faseplassen der en cotangensiell bunt over konfigurasjonsrommet.

I kvantemekanikk uttrykker Heisenbergs usikkerhetsforhold en kvantisering av faseplassen. I den eldre kvanteteorien gjøres dette ved hjelp av Bohr-Sommerfeld-kvantisering . Overganger av fordelingsfunksjoner fra klassisk til kvantemekanisk faseplass (og omvendt) er gitt av Wigner-funksjonen og Weyl-kvantisering .

Eksempel på en fase romanalyse

Faseportrett av den dempede fjærmassoscillatoren med vektorfelt og bane

Faseportrett av Van der Pol-oscillatoren med vektorfelt og typiske baner

Faseplass til et plan pendel med vinkelen på x-aksen og vinkelhastigheten på y-aksen. Faserommet er periodisk med periode med hensyn til vinkelen . Det faste punktet er stabilt, det faste punktet er ustabilt. Separatrixen, som skiller området av "frem og tilbake" pendelbevegelsene (sirkulær bevegelse rundt det stabile faste punktet) fra øvre og nedre område av kontinuerlige høyre og venstre rotasjoner, er vist som en rød linje.${\ displaystyle \ theta}$${\ displaystyle \ omega = {\ dot {\ theta}}}$${\ displaystyle \ theta}$${\ displaystyle 2 \ pi}$${\ displaystyle x_ {1}}$${\ displaystyle x_ {2}}$

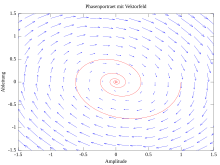
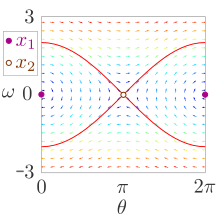
Faseplassportrettet gir muligheten til å grafisk analysere utviklingen av dynamiske systemer over tid. Bare de dynamiske ligningene i systemet kreves for dette; en eksplisitt representasjon av tidsutviklingen, for eksempel ved analytisk løsning av en differensialligning, er ikke nødvendig.

Som et eksempel, noen elementer av faseplassanalyse i et todimensjonalt system , som er definert av differensiallikningene ( , ) ${\ displaystyle {x, y}}$${\ displaystyle x '= {\ frac {\ mathrm {d} x} {\ mathrm {d} t}}}$${\ displaystyle y '= {\ frac {\ mathrm {d} y} {\ mathrm {d} t}}}$

${\ displaystyle x '= f (x, y)}$

${\ displaystyle y '= g (x, y)}$

er beskrevet:

• Tegning i vektorfeltet av dynamikk: For et rutenett av punkter vises bevegelsesretningen i faseområdet med piler. Hvis du følger pilen fra et bestemt startpunkt, kommer du til et nytt punkt der du kan gjenta denne prosedyren. Ved hjelp av vektorfeltet kan du også tegne typiske baner i faseplassportrettet, som hjelper til med å vurdere den kvalitative oppførselen til utviklingen over tid. Med van der Pol-oscillatoren konvergerer for eksempel alle baner mot en grensesyklus , som kan illustreres ved hjelp av prøvebaner i og utenfor syklusen. For enkle dynamiske systemer kan vektorfelt og prøvebaner ofte tegnes inn for hånd; for mer komplekse systemer kan dette gjøres ved hjelp av dataprogrammer.

• Tegning i nulllinjene: En nulllinje beskriver en kurve i faseplass hvor en av de dynamiske variablene ikke endres. Når det gjelder det ovennevnte todimensjonale systemet, er x null kline definert av tilstanden og y null kline er definert av. Disse ligningene kan ofte løses for en av variablene, selv om den generelle dynamikken ikke kan integreres analytisk.${\ displaystyle x '= f (x, y) = 0}$${\ displaystyle y '= g (x, y) = 0}$

• Bestemme faste punkter og deres stabilitet: Som faste punkter kalles stater, som over tid ikke vil endre seg. Slike faste punkter tilsvarer skjæringspunktene til nullinjene i faseplass. I det ovennevnte todimensjonale systemet forklares dette med det faktum at tilstanden er oppfylt ved et slikt kryssingspunkt . En lineær stabilitetsanalyse kan også avgjøre om baner i nærheten av disse punktene tiltrekkes eller frastøtes.${\ displaystyle g (x, y) = f (x, y) = 0}$

• Finne separasjoner: En separatrix (avledet fra det latinske separare "separat") er en kurve eller ( hyper ) overflate som skiller faseplassregioner med ulik (langvarig) oppførsel. For eksempel, hvis det er to faste punkter som tiltrekker seg baner, kan det være en separatrix som skiller de to nedslagsområdene fra hverandre. Med plasseringene og stabiliteten til alle faste punkter eller med vektorfeltet til dynamikken , kan skillematrisene finnes i passende tilfeller uten ytterligere beregninger.

Se også

• Statssum
• Statlig rom (mekanikk) , utvidelse av faseplass med tid
• Diskusjon av faste punkter i autonom differensialligning
• Momentum space , delområde av faseplass
• Resultatplass , settet med alle mulige utfall av et tilfeldig eksperiment

litteratur

• YS Kim, WW Zachary (red.): Fysisk romfysikk. Proc. Første Int. Konf. Physics Phase Space, College Park, Maryland 1986, Lecture Notes in Physics 278, Springer, Berlin 1987, ISBN 3-540-17894-5 .
• Cosmas K. Zachos: Kvantemekanikk i faseplass - en oversikt med utvalgte papirer. World Scientific, Singapore 2005, ISBN 978-981-238-384-6 .
• V. Arnold: Matematiske metoder for klassisk mekanikk. Springer 1989.

weblenker

• Statlig rom. I: Scholarpedia.org. (Engelsk, inkludert referanser).

Individuelle bevis

1. ↑ Imidlertid kan det oppstå at i faseplassportrettet krysser to kurver som separasjonspunktet for et pendel, men skjæringspunktet nås ikke når du beveger deg på banene i systemet.
2. ↑ David Nolte: Den sammenfiltrede fortellingen om faseplass. I: Fysikk i dag. April 2010, s.33.
3. ↑ Ludwig Boltzmann: Videre studier om varmevekt mellom gassmolekyler . I: Sitz.-Ber. Akad. Wiss. Wien (II) . teip 66 , 1872, s. 275-370 . 
4. ↑ James Clerk Maxwell: Om Boltzmanns teorem om gjennomsnittlig fordeling av energi i et system av materielle punkter . I: Transaksjoner fra Cambridge Philosophical Society . teip 12 , 1879, s. 547-570 ( hathitrust.org ). 
5. ^ Arnold: Matematiske metoder for klassisk mekanikk. Springer, 1989, s. 161.
6. ↑ Steven H. Strogatz: Ikke-lineære Dynamics og kaos . Westview Press, 2000, ISBN 978-0-7382-0453-6 , pp. 159 .