Anharmonisk oscillator

Den anharmoniske oscillatoren er et fysisk system som kan vibrere, der gjenopprettingskraften ikke er proporsjonal med avbøyningen fra hvileposisjonen. Som et resultat er den frie svingningen ikke strengt sinusformet . Mekaniske eksempler er pendler (anharmonisitet merkbar med større avbøyning), vippende vibrasjoner (vippingen av en oppreist gjenstand) og hopping av en ball på en flat overflate.

Ved nærmere ettersyn er praktisk talt alle virkelige oscillerende systemer anharmoniske. De fleste nærmer seg imidlertid en harmonisk oscillator , jo mindre avbøyningene fra hvileposisjonen, for da gjelder tilnærmingen av en lineær gjenopprettingskraft alltid bedre (for mekanikk se Hookes lov , matematisk pendel ). I slike anharmoniske oscillatorer er små frie oscillasjoner omtrent sinusformede og har en viss naturlig frekvens , oscillatorens grunnfrekvens .

Sammenlignet med den harmoniske oscillatoren, oppstår det fundamentalt nye fenomener med den anharmoniske oscillatoren:

• Avviket fra den sinusformede formen betyr at svingningen også inneholder harmoniske (akustiske: overtoner ) av den grunnleggende frekvensen. Med harmonisk eksitasjon med den grunnleggende frekvensen dør de ikke selv etter den forbigående prosessen , men fortsetter å vibrere sammen med den fundamentale svingningen.
• Når det gjelder en asymmetrisk kraftlov, forskyves svingningens sentrum sammenlignet med hvileposisjonen. Dette skjer f.eks. B. i vibrasjonene mellom atomene i den faste kroppen og er årsaken til deres termiske ekspansjon.
• I tilfelle av periodisk eksitasjon, den resulterende tvungen svingning ikke bare inneholder det eksitasjon og egenfrekvenser, slik tilfellet er med den harmoniske oscillator, men også deres differansefrekvens og sumfrekvens, så vel som alle andre heltall kombinasjoner derav. Dette brukes til tekniske formål. B. i ikke-lineær optikk med frekvensen doblet med laserlys .
• Ved ekstern eksitasjon med periodisk kraft, kan den anharmoniske oscillatoren også reagere med en kaotisk bevegelse hvis de opprinnelige forholdene er valgt tilsvarende eller hvis parametrene er utenfor visse grenser (f.eks. Hvis dempingen er for lav ). Se også: dobbel pendel

Ligning av bevegelse

Illustrasjon av den anharmoniske kraftloven F (x) i eksempel A (rød) og B (grønn) for saken k = 1 og l = 0,2 , sammenlignet med den harmoniske kraftloven F (x) = - kx (blå). I tillegg vises de tilknyttede potensialene V (x) med F (x) = - d V / d x i den grå boksen.

Baner for den harmoniske oscillatoren og de to diskuterte anharmoniske oscillatorer i sammenligning for parametrene m = k = 1, l = 0,2, c = 0 og forskjellige utgangsbetingelser og . Høyre kolonne viser faseplassportretter av de tre oscillatorene.${\ displaystyle x (0)}$${\ displaystyle m \ cdot {\ dot {x}} (0) = p (0)}$

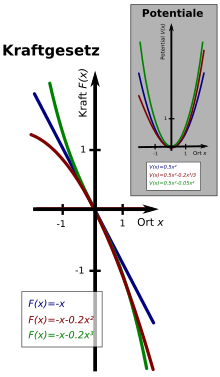
Det er et stort antall forskjellige anharmoniske oscillatorer og tilsvarende mange bevegelsesligninger. Det er også forskjeller avhengig av om problemet kommer fra mekanikk, akustikk eller elektrisk . Felles for dem er at deres gjenopprettingskraft ikke bare avhenger lineært av nedbøyningen , slik tilfellet er med den harmoniske oscillatoren , men også av høyere krefter ("ikke-lineær kraftlov"). I figuren motsatt er de enkleste eksemplene vist sammen med den omtrentlige lineære kraftloven (blå rett linje): ${\ displaystyle F (x) = - kx}$${\ displaystyle x}$${\ displaystyle x}$

A) En enkel asymmetrisk kraftlov (rød kurve på bildet til høyre) leser . ${\ displaystyle F (x) = - kx-lx ^ {2}}$

En transformasjon viser at det ikke-lineære begrepet i stadig større grad svekker gjenopprettingskraften på den ene siden og styrker den på den andre siden, forutsatt at avbøyningene ikke er for store ( ). Som du kan se fra banene i den andre figuren, fører dette til en sterkere avbøyning av oscillatoren i retning av den svekkede gjenopprettingskraften og til en redusert periode sammenlignet med den harmoniske oscillatoren. En slik asymmetrisk kraftlov kan brukes som en annen tilnærming (etter den lineære kraftloven) til Morse-potensialet nevnt nedenfor i molekylærfysikk .${\ displaystyle F (x) = - kx (1 + {\ tfrac {l} {k}} x)}$${\ displaystyle | {\ tfrac {l} {k}} x | <1}$ ${\ displaystyle x (t)}$

B) En enkel symmetrisk kraftlov (grønn kurve på bildet til høyre) lyder . ${\ displaystyle F (x) = - kx-lx ^ {3}}$

Avhengig av tegnet på øker gjenopprettingskraften stadig sterkere ( ) eller svakere ( ) sammenlignet med den harmoniske oscillatoren . I det første tilfellet oppstår svingningene raskere med samme amplitude, i det andre tilfellet saktere.${\ displaystyle l}$${\ displaystyle l> 0}$${\ displaystyle l <0}$

For eksempel er dette kraftloven for en tilnærming for tyngdekraften eller matematisk pendel , hvis svingningsperiode øker med økende amplitude. I dette tilfellet står størrelsen for den dimensjonsløse avbøyningsvinkelen til pendelen. En slik tilnærming oppnås hvis gjenopprettingskraften til den matematiske pendelen er utviklet i en Taylor-serie opp til tredje rekkefølge i : ${\ displaystyle l = -k / 6}$${\ displaystyle x}$${\ displaystyle F (x) = - k \ cdot \ sin x}$${\ displaystyle x}$

${\ displaystyle F (x) = - k \ cdot \ sin x \ approx \ underbrace {-k \ cdot x + {\ frac {k} {6}} x ^ {3}} _ {\ text {1. og tredje rekkefølge}} - {\ frac {k} {120}} x ^ {5} + \ ldots}$

De bevegelseslikningene med demping sikt da resultere fra Newtons lov${\ displaystyle c {\ dot {x}}}$

${\ displaystyle m {\ ddot {x}} = - c {\ dot {x}} + F (x)}$

der det første og det andre avledede av funksjonen med hensyn til tid betegner: ${\ displaystyle {\ dot {x}}}$${\ displaystyle {\ ddot {x}}}$${\ displaystyle x (t)}$${\ displaystyle t}$

Sak A :${\ displaystyle m {\ ddot {x}} + c {\ dot {x}} + kx + lx ^ {2} = 0}$

Sak B :${\ displaystyle m {\ ddot {x}} + c {\ dot {x}} + kx + lx ^ {3} = 0}$

Den lineære kraftloven og differensialligningen til den dempede harmoniske oscillatoren oppnås igjen for i begge tilfeller. Selv for små avbøyninger er løsningen av den anharmoniske oscillatoren igjen nesten harmonisk, som de første banene i figuren til høyre viser. ${\ displaystyle l = 0}$

Superposisjonsprinsippet er ugyldiggjort av ikke-lineariteten til differensialligningene . Dette betyr at ikke hvert multiplum av en løsning også er en løsning av differensiallikningen, og mer generelt, at med to løsninger er ikke alle lineære kombinasjoner også en løsning (hvor noen faste tall er). Løsningen på bevegelsesligningen er vanligvis en elliptisk integral og kan derfor ikke representeres i en lukket form med elementære funksjoner. Denne artikkelen fokuserer på periodiske bevegelser av den anharmoniske oscillatoren. Dempingen forsømmes steder, dvs. H. sett. Dette er den eneste måten periodiske bevegelser i streng forstand oppstår hvis ingen ytre kraft virker. For informasjon om kaotiske bevegelsesformer, se kaosforskning og faglitteraturen spesifisert der. ${\ displaystyle \ alpha \ cdot x (t)}$${\ displaystyle x (t)}$${\ displaystyle x_ {1} (t), \; x_ {2} (t)}$ ${\ displaystyle x (t) = \ alpha _ {1} \ cdot x_ {1} (t) + \ alpha _ {2} \ cdot x_ {2} (t)}$${\ displaystyle \ alpha, \, \ alpha _ {1}, \, \ alpha _ {2}}$${\ displaystyle c = 0}$

Omtrentlig løsning

I tilfelle en svak anharmonisk forstyrrelse, dvs. H. eller løsningen kan oppnås ved beregning av forstyrrelse . For å gjøre dette gir man en interferensparameter i form av en kraftserie : ${\ displaystyle | kx | \ gg | lx ^ {2} |}$${\ displaystyle | kx | \ gg | lx ^ {3} |}$${\ displaystyle x}$${\ displaystyle \ epsilon = -l / m}$

${\ displaystyle {\ begin {align} x (t) & = x_ {0} (t) & + & \; \ epsilon \ cdot x_ {1} (t) & + & \; \ epsilon ^ {2} \ cdot x_ {2} (t) & + & ldots \\\ omega & = \ omega _ {0} & + & \; \ epsilon \ cdot \ omega _ {1} & + & \; \ epsilon ^ {2 } \ cdot \ omega _ {2} & + & \ ldots \ end {align}}}$

Det første begrepet er løsningen (tilpasset de innledende forholdene) for det harmoniske tilfellet , f.eks. B. hvis oscillatoren for øyeblikket frigjøres under nedbøyningen med hastighet og har grunnfrekvensen . ${\ displaystyle l = 0}$${\ displaystyle x_ {0} (t) = A \ cos \ omega _ {0} t}$${\ displaystyle t = 0}$${\ displaystyle x = A}$${\ displaystyle {\ dot {x}} = 0}$${\ displaystyle \ omega _ {0} = {\ sqrt {k / m}}}$

Etter å ha satt inn i bevegelsesligningen, der er uttrykt av en potensrekke i resultater , må koeffisientene som alle settes lik null. Dette gir differensialligninger for de individuelle tilnærmingsfunksjonene som må løses rekursivt. Konkret, differensialligningen for formen av bevegelsesligningen for en harmonisk oscillator eksitert i tvangssvingninger av en ekstern kraft gitt av de forrige . ${\ displaystyle x (t)}$${\ displaystyle l}$${\ displaystyle \ epsilon}$${\ displaystyle \ epsilon}$${\ displaystyle x_ {i} (t)}$${\ displaystyle x_ {i + 1} (t)}$${\ displaystyle x_ {i}}$

I tilfelle A følger i første trinn

${\ displaystyle x (t) = A \ cos \ omega _ {0} t + \ epsilon {\ frac {A ^ {2}} {6 \ omega _ {0} ^ {2}}} (3-4 \ cos \ omega _ {0} t + \ cos 2 \ omega _ {0} t) + \ epsilon ^ {2} (\ ldots) + \ ldots}$

Den doblede grunnfrekvensen forekommer allerede her. Den matematiske årsaken til dette kan spores tilbake til forekomsten av det kvadratiske begrepet i bevegelsesligningen, som er linearisert av den trigonometriske identiteten . Ytterligere tilnærminger resulterer i summander med tilsvarende høyere multipler av grunnfrekvensen, dvs. et helt spektrum av harmoniske. ${\ displaystyle x ^ {2} (t)}$${\ displaystyle 2 \ cos ^ {2} \ phi = \ cos (2 \ phi) +1}$

I tilfelle B er det første trinnet en ustabil løsning fordi den inneholder et begrep som er for proporsjonalt, men dette kan elimineres hvis det er angitt. I den første tilnærmingen er svingningsfrekvensen avhengig av amplituden (som i tilfelle A bare i det andre trinnet). ${\ displaystyle x_ {1} (t)}$${\ displaystyle t \ cos \ omega _ {0} t}$${\ displaystyle \ omega _ {1} = - {\ tfrac {3} {8}} {\ tfrac {A ^ {2}} {\ omega _ {0}}}}$${\ displaystyle \ omega}$${\ displaystyle A}$

applikasjoner

Fjærer som faktisk er innebygd i tekniske enheter, har generelt et lineært forhold mellom å gjenopprette kraft og avbøyning bare innenfor visse grenser, noen ganger også ment av designet. Dynamikken til et system med slike fjærer følger deretter de ikke-lineære bevegelsesligningene som introdusert ovenfor.

Morse-potensialet (blått) sammenlignet med kvadratpotensialet til den harmoniske oscillatoren (grønn). Energinivåene som er like langt ( ) for den harmoniske oscillatoren , men med Morse-kodepotensial, har imidlertid mindre og mindre avstand med økende energi vises også. ( er bindingsenergien, beregnet fra minimum av potensialet. Er dissosiasjonsenergien faktisk nødvendig for å unnslippe fra det potensielle trau, på grunn av nullpunktet er energien ( ) mindre enn .)${\ displaystyle \ hbar \ omega}$${\ displaystyle D_ {e}}$${\ displaystyle D_ {0}}$${\ displaystyle \ nu = 0}$${\ displaystyle D_ {e}}$

Viktige anvendelser for anharmoniske svingninger finnes i molekylærfysikk for oscillasjon av diatomiske molekyler, eller i faststoffysikk for varmeinduserte svingninger av atomer. Anharmonisiteten er dannet av de forskjellige effektene når de nærmer seg (elektrostatisk frastøting, delvis skjermet av elektronene i atomskallet , men forsterket av Pauli-prinsippet ) og fjerning (gjenopprettingskraft på grunn av atomens kovalente binding ) av atomkjernene. Som vist i figuren til høyre, kan slike svingninger beregnes for eksempel i et morse-potensial .

Tvungne anharmoniske vibrasjoner

Når man beveger seg under påvirkning av en tidsavhengig ekstern kraft , er anharmoniske og harmoniske oscillatorer fundamentalt forskjellige fra hverandre. For eksempel, selv etter slutten av en forbigående prosess, kan den anharmoniske oscillatoren svinge med andre frekvenser enn de som er representert i den spennende kraften. Selv med langsomme variasjoner i eksiteringsfrekvensen, kan plutselige endringer i amplituden oppstå. Når det gjelder koblede anharmoniske oscillatorer, kan en minimal, knapt målbar endring i frekvens eller amplitude føre til store endringer i oppførselen til alle koblede elementer. Disse fenomenene er også av stor praktisk interesse, siden virkelige oscillatorer bare oppfører seg i harmoni så lenge visse grenser for avbøyning og / eller frekvens overholdes. ${\ displaystyle F (t)}$

Disse fenomenene kan generelt spores tilbake til den ikke-lineære formen av bevegelsesligningen, noe som betyr at superposisjonsprinsippet ikke lenger kan brukes her. Noen av konsekvensene:

• Det er ingen generelt gyldig løsningsmetode som med de tvungne svingningene til den harmoniske oscillatoren. Man må numerisk integrere bevegelsesligningen eller bruke analytiske løsninger som bare kan oppnås under omtrentlige antagelser.
• Den forbigående prosessen (med periodisk eksitasjon) er ikke gitt ved overstillingen av den stasjonære svingningen med en fri svingning.
• Den jevne stasjonære svingningen er ikke alltid uavhengig av de opprinnelige forholdene.
• Etter Fourier-transformasjon forblir bevegelsesligningene for forskjellige frekvenser koblet til hverandre.

Amplitude hopper

Tenk som eksempel på den symmetriske kraftloven (sak B ovenfor ): Bevegelsesligningen lyder (etter divisjon av , med og ): ${\ displaystyle m}$${\ displaystyle \ gamma = {\ frac {c} {2m}}}$${\ displaystyle f (t) = {\ frac {F (t)} {m}}}$

${\ displaystyle {\ ddot {x}} + 2 \ gamma {\ dot {x}} + \ omega _ {0} ^ {2} x + \ epsilon x ^ {3} = f (t)}$

Basert på antagelsen om en stasjonær harmonisk svingning

${\ displaystyle x (t) = A \ cdot \ sin \ Omega t}$

resultater fra dette for årsakskraften

(**) .${\ displaystyle \; f (t) = (\ omega _ {0} ^ {2} - \ Omega ^ {2}) A \ sin \ Omega t \; + \; 2 \ gamma \ Omega A \ cdot \ cos \ Omega t \; + \; \ epsilon A ^ {3} \ left ({\ tfrac {3} {4}} \ sin \ Omega t - {\ tfrac {1} {4}} \ sin (3 \ Omega t) \ høyre)}$

Den delen av kraften som svinger med den kommer fra deformasjonen . Denne andelen blir neglisjert i det følgende. Kraften kan deretter tilnærmes ${\ displaystyle 3 \ Omega}$${\ displaystyle \ sin ^ {3} \ phi \ equiv {\ tfrac {3} {4}} \ sin \ phi - {\ tfrac {1} {4}} \ sin (3 \ phi)}$

${\ displaystyle f (t) = f_ {0} \ cdot \ sin (\ Omega t + \ varphi)}$

oppsummer, slik at her genererer en kraft som oscillerer harmonisk med frekvensen en harmonisk svingning av samme frekvens. Det er et faseskift og amplituden til kraften gjennom ${\ displaystyle \ Omega}$${\ displaystyle \ varphi}$

${\ displaystyle f_ {0} ^ {2} = \ left ((\ omega _ {0} ^ {2} - \ Omega ^ {2}) A \; + \; {\ tfrac {3} {4}} \ epsilon A ^ {3} \ right) ^ {2} \; + \; 4 \, \ gamma ^ {2} \ Omega ^ {2} A ^ {2}}$

gitt. Det er sant at denne ligningen ikke kan endres i den formen som er vanlig for resonanskurven . Det kan imidlertid løses, og forholdet mellom eksiteringsfrekvensen og den stasjonære svingningsamplituden (for kraftamplituden gitt av) oppnås i form: ${\ displaystyle A (\ Omega)}$${\ displaystyle \ Omega ^ {2}}$${\ displaystyle \ Omega}$${\ displaystyle A}$${\ displaystyle f_ {0}}$

${\ displaystyle (\ Omega _ {1/2}) ^ {2} = \ omega _ {0} ^ {2} -2 \ gamma ^ {2} \; + \; {\ tfrac {3} {4} } \ epsilon A ^ {2} \; \ pm \; {\ sqrt {{\ frac {f_ {0} ^ {2}} {A ^ {2}}} + \; 4 \, \ gamma ^ {2 } \ left (\ gamma ^ {2} \ omega _ {0} ^ {2} - {\ tfrac {3} {4}} \ epsilon A ^ {2} \ right)}}}$.

De to løsningene som oppstår her ved å løse en kvadratisk ligning, uttrykker at generelt to eksitasjonsfrekvenser fører til den samme amplituden til den stasjonære svingningen, som det er tilfellet med den harmoniske oscillatoren til venstre og høyre for resonanstoppen. For det harmoniske tilfellet , stemmer denne formelen overens med resonanskurven til de harmoniske tvungne vibrasjonene, som har sitt maksimale amplitude ved og faller symmetrisk på begge sider. Det som er nytt med den anharmoniske oscillatoren er at resonansfrekvensen skifter med økende amplitude (betegnelse i formelen). Som et resultat kan hele resonanstoppen i grafen til resonanskurven kurve på en slik måte at den antar en S-form i visse frekvensområder, dvs. viser opptil tre forskjellige mulige verdier for steady-state amplitude til tross for samme kraftamplitude og eksitasjonsfrekvens . Hvis et slikt område oppnås med langsom, jevn variasjon av eksiteringsfrekvensen, hopper amplituden fra en gren av resonanskurven til en annen: svingningen "tips". ${\ displaystyle \ Omega _ {1/2}}$${\ displaystyle \ epsilon = 0}$${\ displaystyle \ Omega ^ {2} = \ omega _ {0} ^ {2} -2 \ gamma ^ {2}}$${\ displaystyle {\ tfrac {3} {4}} \ epsilon A ^ {2}}$${\ displaystyle A (\ Omega)}$${\ displaystyle f_ {0}}$${\ displaystyle \ Omega}$${\ displaystyle A}$

Subharmonisk eksitasjon

I forrige avsnitt ble et bidrag til kraften som svinger med frekvens ganske enkelt utelatt i ligning (**). Dette er ikke alltid berettiget, fordi dette bidraget også kan spille hovedrollen under visse forhold. Hvis det gjelder ${\ displaystyle 3 \ Omega}$

${\ displaystyle \ gamma = 0}$   og   ,${\ displaystyle (\ omega _ {0} ^ {2} - \ Omega ^ {2}) \; + \; {\ frac {3} {4}} \ epsilon A ^ {2} = 0}$

da forsvinner alle med periodiske termer fra ligning (**) . Det forblir: ${\ displaystyle \ Omega}$

${\ displaystyle x (t) = A \ cdot \ sin \ Omega t}$

er en løsning på ekstern styrke

${\ displaystyle f (t) = \ epsilon A ^ {3} {\ frac {1} {4}} \ sin (3 \ Omega t)}$.

Eksempel: Den matematiske pendelen med grunnfrekvens ( akselerasjon på grunn av tyngdekraften, pendelens lengde), kraftloven tilnærmet ved å velge parameteren , drives av en ekstern kraft ${\ displaystyle \ omega _ {0} = {\ sqrt {g / L}}}$${\ displaystyle g}$${\ displaystyle L}$${\ displaystyle \ epsilon = - \ omega _ {0} ^ {2} / 6}$

${\ displaystyle F (t) = - {\ frac {1} {24}} m \ omega _ {0} ^ {2} \ cdot \ sin (3 \ Omega t) \ quad {\ text {with}} \ quad \ Omega = {\ sqrt {7/8}} \ omega _ {0}}$.

Da svinger den med amplitude og en tre ganger redusert frekvens som . For å kunne observere denne oppførselen, må man imidlertid enten oppfylle de riktige startbetingelsene eller vente på at ytterligere naturlige vibrasjoner skal avta, noe som kan ta veldig lang tid på grunn av antagelsen om ubetydelig lav demping. ${\ displaystyle A = 1 \ ca 57 ^ {\ circ}}$${\ displaystyle x (t) = A \ sin (\ Omega t)}$

Intermodulasjon

Intermodulasjon beskriver fenomenet at oscillatoren, når den blir begeistret med to frekvenser , reagerer med en oscillasjon der kombinasjonsfrekvenser ( og hele tall) også er representert. Under den forbigående prosessen, som vanligvis bare varer kort tid på grunn av demping, er slike frekvensmultipler og kombinasjonsfrekvenser også til stede i forhold til grunnfrekvensen . I akustikk kan de fremstå som hørbare toner, som er forårsaket av at trommehinnen eller en høyttalermembran er begeistret utover avbøyningen som en lineær kraftlov gjelder for gjenopprettingsstyrken. ${\ displaystyle \ Omega _ {1} \ neq \ Omega _ {2}}$${\ displaystyle \ Omega = | n \ Omega _ {1} \; \ pm \; m \ Omega _ {2} |}$${\ displaystyle n}$${\ displaystyle m}$${\ displaystyle \ omega _ {0}}$

litteratur

Friedhelm Kuypers: Klassisk mekanikk . 8. utgave. Wiley-VCH, Weinheim 2007, ISBN 978-3-527-40721-7 . 

Se også

• Dobbeltbrønnspotensial
• Duffing oscillator
• Van der Pol-systemet
• Metode for harmonisk balanse
• Harmonisk oscillator
• Harmonisk oscillator (kvantemekanikk)
• Forstyrrelsesteori (kvantemekanikk)