Konseptuell skriving

Tittelsiden til den konseptuelle skrivingen

Den sikt skriving er en smal, kun om lag åtti side omfattende bok ved Jena matematikeren og filosofen Gottlob Frege på logikk . Den ble utgitt i 1879 med undertittelen "En av det aritmetiske simulerte formelspråket for ren tanke" og regnes generelt for å være den viktigste publikasjonen innen logikk siden Aristoteles ' Organon .

I denne boka lyktes Frege for første gang i å formalisere klassisk predikatlogikk og dermed den første formaliseringen av en logikk der en tilstrekkelig stor del av matematikken, men også av det naturlige språket, kunne komme til uttrykk. Sammen med George Booles matematiske analyse av logikk fra 1847 markerer begrepsskrivingen derfor begynnelsen på moderne formell logikk. Begrepet konseptuell skriving brukes også om den logiske kalkulasjonen definert av Frege så vel som for Freges logiske notasjon . Frege designet begrepet manus for å støtte sin forskning på grunnleggende matematikk.

Freges kalkulus introduserte den universelle kvantifisereren og flersifrede predikater (relasjoner) for første gang . Det er en klassisk andreordens predikatlogisk kalkulator med identitet , men i en todimensjonal notasjon som er idiosynkratisk sammenlignet med dagens stavemåter.

Plasseringen av den konseptuelle skrivingen i de komplette verkene til Freges

Til tross for sin epokegjørende betydning er ikke begrepet Freges hovedverk. Dette ble fulgt i 1884 av The Fundamentals of Arithmetic og i 1893 og 1903 av de to volumene av Basic Laws of Arithmetic , som på grunn av deres størrelse kan betraktes som Freges hovedverk.

Frege rundt 1880, omtrent den tiden begrepet skriving ble publisert

Freges primære mål var å identifisere matematikk som en del av logikken, dvs. å vise at alle matematiske proposisjoner kan stamme fra noen få rent logiske aksiomer (jf. Logikk ). Dette selskapet lovte bare hvis det var et middel tilgjengelig der integriteten til en nøkkelring kunne verifiseres uten tvil. Siden den tradisjonelle aristoteliske logikken ( syllogistikk ) viste seg å være ubrukelig for dette formålet, tok Frege først på seg oppgaven med å lage en ny, mer passende logikk. Dette ble gjort i form av konseptuell skriving . For Frege var den konseptuelle skrivingen derfor bare det første trinnet på vei mot en fullstendig formalisering av matematikken som helhet, som han delvis gjennomførte i de grunnleggende regningslovene for tallteori . Freges logistiske program mislyktes opprinnelig (før utgivelsen av andre bind av grunnloven ) på grunn av Russells antinomi , men det ble videreført av Bertrand Russell , Rudolf Carnap og andre.

Imidlertid var terminologien på ingen måte ment utelukkende for bruk i matematikk. Tvert imot, Frege plasserte skrivingen i forordet uttrykkelig i sammenheng med Leibnizs idé om en lingua characterica universalis , et universelt språk som skulle representere et ordnet system av alle konsepter basert på en matematisk modell. Freges font, presentert i 1879, var ment å danne det logiske hjertet til et slikt universelt språk. Det kan antas at begrepet konseptuell skriving er lånt fra en avhandling av Friedrich Adolf Trendelenburg om Leibniz utkast til dette universelle språket, som Frege siterer i forordet. Forresten var ordet "concept writing " i vanlig bruk rundt begynnelsen av 1900-tallet som en germanisering av " ideografi ".

notasjon

Innføring av logiske symboler i konseptuell skriving .
Klikk på forhåndsvisningen for å åpne den.

Frege brukte i Begriffsschrift en spesiallaget av ham notasjon (Notasjon) for uttrykk for proposisjons- og predikatlogikken . Notasjonen av den konseptuelle skrivingen er en grafisk, todimensjonal representasjon der formler er forbundet med hverandre ved hjelp av horisontale og vertikale linjer. Den bruker tegn på negasjonen og det betingede som det proposisjonslogiske elementet og den universelle kvantifisereren som predikatlogikkelementet. Akkurat som den polske notasjonen - om enn lineær, endimensjonal og derfor mye mer plassbesparende - mye senere , kommer den konseptuelle notasjonen seg uten parentes.

syntaks

Den Begriffsschrift vet bare to syntaktiske grunnleggende elementer: funksjonelle uttrykk og egennavn, både av variablene kan være representert. Alle syntaktiske operasjoner følge ordningen funksjon - argument - verdi: Ved å anvende en funksjon med n frie stillinger til n argumenter, er en viss verdi av funksjonen oppnådd.

Mer om begrepet funksjon: Hvis du for eksempel i det komplekse uttrykket '1 × 1' erstatter begge forekomster av talltegnet '1' med variablene 'n' eller 'm', får du funksjonsuttrykket 'n × m'. Variablene gjør det klart at begrepet "umettet" er, som Frege sier: i denne formen betegner det ikke et objekt, men må fullføres av to argumenter. Fornyet erstatning av tall for variablene gir en rekke aritmetiske termer , f.eks. B. '1 × 1', '1 × 2', '2 × 1' osv. De forskjellige mulige erstatningene for variablene er argumentuttrykk . Det som betegnes med det komplekse uttrykket, er verdien av funksjonen. For eksempel er verdien av funksjonen n × m for argument 2 og 3 tallet 6.

Denne grunnleggende ordningen er på ingen måte begrenset i anvendeligheten til matematikkfeltet: Hvis for eksempel i 'The Conqueror of x' erstattes variabelen 'x' med 'Gallia', får funksjonen verdien Julius Caesar. I følge Frege er predikater også funksjoner: Funksjonen uttrykt av 'x erobret Gallia' tar verdien sant for argumentet Julius Caesar og verdien falsk for argumentet Hannibal. Erstatningen av subjekt-predikatformen med dommerens funksjonsargumentform var allerede et betydelig fremskritt sammenlignet med tradisjonell logikk, fordi det gjorde det mulig å formulere en logikk av relasjoner: moderne logikk vet også (i motsetning til syllogistikk) To- og flersifrede predikater (relasjonsuttrykk), for eksempel 'x elsker y', 'x står mellom y og z' osv. (Se også Logikk - Klassisk logikk .)

Sannhetsfunksjonalitet

Frege tok nå alle sammensatte uttrykk som resultat av å bruke en funksjon på argumenter; spesielt behandlet han også disse uttrykkene som funksjonelle uttrykk som nå er kjent som snekkere . Argumentene deres er utsagn, sannhetsverdiene sanne og falske, som Frege kaller "den sanne" og "den falske". For å indikere betydningen av et binde, er det tilstrekkelig å definere forholdene der en påstand med denne binde blir sant eller usant. I dag kalles denne forbindelsen sannhetsfunksjonalitet , og sannhetsbetingelsene er vanligvis gitt i form av såkalte sannhetstabeller . Sannhetsfunksjonaliteten er en viktig forutsetning for etablering av en utvidende semantikk som utviklet av Alfred Tarski på 1930-tallet.

Innholdslinje og dommerlinje

Den horisontale "innholdslinjen" betyr i den konseptuelle skrivingen at det som følger den er et "vurderbart innhold" (når det gjelder sannhet eller løgn), i moderne terminologi en påstand som kan være sann eller usann. Innholdslinjen avgjør ikke om en påstand er sann; det hevdes ikke, men bare "settes i rommet" som potensielt sant eller usant:

Husk at du ville være en absurd forbindelse vises som "- 2" i Begriffsschrift ikke-syntaks, grunnlovsstridig; deres verdi ville være feil. Dette har å gjøre med at Freges konseptuelle skriving er ren begrepslogikk; Uttalelser er også entallbetegnelser, til en viss grad forskjellige navn for de to sannhetsverdiene.

Den vertikale "dommen" foran innholdslinjen indikerer at innholdet er sant:

Frege sa at innholdet ble uttrykt med "assertiv kraft".

Junctures

Konseptuell skriveanvisning: proposisjonslogikk

Av de fem vanligste i dag brukte Frege 'ikke', 'og', 'eller', 'hvis - da', 'nøyaktig hvis' bare to: 'ikke' ( negasjon ) og 'hvis - da' ( implikasjon eller Betinget). Negasjonen vises ved å legge til en liten vertikal linje i innholdslinjen. Negasjonen "ikke A" ( ) uttrykkes som følger: ${\ displaystyle \ lnot A}$

Verdien av denne funksjonen er sant hvis og bare hvis sannhetsverdien til '- A' ikke er sant, ellers er den falsk.

Implikasjonen (les: 'hvis B, så A') gjennomføres i den konseptuelle skrivingen ${\ displaystyle B \ rightarrow A}$

uttrykte. Frege skrev om betydningen av denne kombinasjonen av tegn:

I en formulering som ser ut til å være uvanlig i dag, er dette sannhetsforholdene for den materielle implikasjonen : Implikasjonen er bare falsk hvis forgjengeren er sann og den følgende er falsk.

Disjunksjon ('eller') og konjunktjon ('og') kan uttrykkes ved å kombinere disse to skjøtene: disjunksjonen blir gjennom

- - Uttrykt sammenhengen av${\ displaystyle \ neg B \ rightarrow A}$

- . Siden Freges logikk er et begrepslogikk der uttalelser også er enestående termer, fungerer også "tegn på innholdslikhet" (identitetstegn) som et uttrykk for materiell ekvivalens . ${\ displaystyle \ neg (B \ rightarrow \ neg A)}$${\ displaystyle \ equiv}$

Kvantifiserere

Konseptuell notasjon: predikatlogikk

Som en universell kvantifier bruker Frege en innrykk ("hulrom") i innholdslinjen, der variabelen som skal bindes er skrevet inn i (se tilstøtende grafikk). På grunn av ekvivalensen som gjelder i klassisk predikatlogikk

${\ displaystyle \ eksisterer xF (x) \ leftrightarrow \ lnot \ forall x \ lnot F (x)}$

en egen eksistensiell kvantifisering er ikke nødvendig; innholdet kan uttrykkes av den universelle kvantifisereren og negatoren.

Følgende eksempel viser utsagnet "for hver x med eiendommen F er det et y som x er relatert til R" (f.eks. "Hver person har en mor"). Den illustrerer de to viktigste prestasjonene ved konseptuell skriving, som skiller den fra tradisjonell syllogistikk så vel som fra moderne logisk algebra : nestede kvantifiserere ("for hver x er det en y") og flersifrede predikater ("R (x, y)" ).

Fra denne uttalelsen følger det med aksiom 9 ( se nedenfor ):

Fra dette, i forbindelse med utsagnet "F (c)" ved hjelp av regelen modus ponens ( se nedenfor ), kan utsagnet "det er et y som c er i R" avledes:

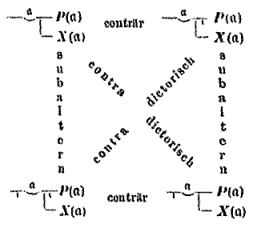
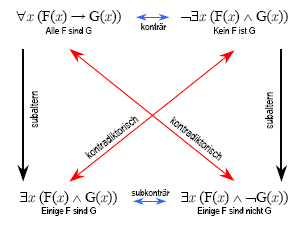
Kvantifiseringslogikken tillater (forutsatt at emnet ikke er tomt) alle slutninger av tradisjonell logikk. Figuren nedenfor viser den " logiske firkanten " til venstre fra den opprinnelige utgaven av begrepet script , til høyre i moderne notasjon for sammenligning:

   

Det faktum at Frege sier "motsatt" i stedet for "underkontra" i bunnlinjen, er åpenbart en oversikt.

Se også tabelloversikten over notasjonen på slutten av artikkelen.

Aksiomsystemet for konseptuell skriving

Etter forklaringene på notasjonen i første kapittel, fortsetter Frege i andre kapittel med overskriften "Presentasjon og avledning av noen dommer av ren tenkning" for å bevise noen logisk sanne proposisjoner på grunnlag av noen få aksiomer.

Frege begrunnet ikke-formelt sine ni aksiomer ved å forklare hvorfor de er sanne i sin tiltenkte tolkning. Oversatt til moderne notasjon er aksiomene:

1. ${\ displaystyle \ vdash \ \ A \ til \ venstre (B \ til A \ høyre)}$
2. ${\ displaystyle \ vdash \ \ (A \ til (B \ til C)) \ \ til \ \ venstre (\ venstre (A \ til B \ høyre) \ til \ venstre (A \ til C \ høyre) \ høyre) }$
3. ${\ displaystyle \ vdash \ \ \ venstre (D \ til \ venstre (B \ til A \ høyre) \ høyre) \ \ til \ \ venstre (B \ til \ venstre (D \ til A \ høyre) \ høyre)}$
4. ${\ displaystyle \ vdash \ \ \ left (B \ til A \ høyre) \ \ til \ \ left (\ lnot A \ til \ lnot B \ høyre)}$
5. ${\ displaystyle \ vdash \ \ \ lnot \ lnot A \ til A}$
6. ${\ displaystyle \ vdash \ \ A \ to \ lnot \ lnot A}$
7. ${\ displaystyle \ vdash \ \ \ left (c \ equiv d \ right) \ to \ left (F (c) \ equiv F (d) \ right)}$
8. ${\ displaystyle \ vdash \ \ c \ equiv c}$
9. ${\ displaystyle \ vdash \ \ \ left (\ forall xF (x) \ right) \ \ to \ F (c)}$

I Freges egen nummerering er dette setninger 1, 2, 8, 28, 31, 41, 52, 54 og 58. (1) - (3) relaterer seg til den materielle implikasjonen, (4) - (6) negasjonen. (7) og (8) gjelder identitet: (7) er Leibniz identitetsprinsipp . (8) etterlyser refleksivitet av identitet. (9) tillater overgangen fra en alt-kvantifisert uttalelse til enhver forekomst. Alle andre proposisjoner er hentet fra disse aksiomene.

Den konseptuelle skrivingen har tre regler for slutning . To av dem, modus ponens og generaliseringsregelen, er nevnt eksplisitt. Ponens-modus tillater overgang fra og til . Generaliseringsregelen tillater overgangen fra til hvis variabelen 'x' ikke vises i P. Den tredje regelen, ikke eksplisitt nevnt, er et substitusjonsprinsipp . ${\ displaystyle \ vdash A \ til B}$${\ displaystyle \ vdash A}$${\ displaystyle \ vdash B}$${\ displaystyle \ vdash P \ til A (x)}$${\ displaystyle \ vdash P \ to \ forall xA (x)}$

Fragmentet av kalkulatoren gitt i notasjonen som tilsvarer en predikatlogikk på det første nivået er komplett og fri for motsetninger . Det var ikke før systemet ble utvidet til å omfatte en teori om omfanget av begrepene, som Frege senere utførte i de grunnleggende aritmetiske lovene , som førte til inkonsistens .

Det tredje kapittelet har tittelen “Noen fra en generell serieundervisning”. De viktigste resultatene gjelder arven til et trekk på rad og rekkefølgen på rad. Hvis en relasjon R er gitt, er en eiendom F ifølge Frege arvelig i R-serien hvis og bare hvis:

${\ displaystyle \ forall x \ forall y \ (F (x) \ land xRy \ to F (y))}$

Deretter definerer Frege: b følger a i R-serien hvis og bare hvis b har alle arvelige egenskaper i R-serien som alle x har med aRx. Hvis du skriver R * for dette forholdet av følgende i R-serien, kan Freges definisjon gjengis som følger:

${\ displaystyle aR ^ {\ ast} b \ equiv \ forall F [\ forall x (aRx \ to F (x)) \ wedge \ forall x \ forall y (F (x) \ wedge xRy \ to F (y) ) \ til F (b)]}$

Kortere, der "Erbl (F, R)" skal bety "F er arvelig i R-serien":

${\ displaystyle aR ^ {\ ast} b \ equiv \ forall F [\ forall x (aRx \ to F (x)) \ wedge Erbl (F, R) \ to F (b)]}$

Om denne R * -relation Frege beviser noen teoremer som viser at det er en ordre forhold . Disse hensynene er åpenbart ment som forarbeid for de to påfølgende verkene om grunnleggende tallteori. Hvis man betrakter forholdet y = x + 1 som xRy, er 0R * y (eller 1R * y) egenskapen til y som et naturlig tall .

Mottak og effekt

Den Begrepet skriftlig funnet en bemerkelsesverdig kjølig mottakelse i begynnelsen. Ikke minst på grunn av sin uvanlige og vanskelige å lese symbolikk, ser det ut til at allmennheten i utgangspunktet har tatt lite merke til den. Tenoren i samtidsanmeldelser var for det meste dempet til kritisk. Bekymringer for den omfattende, vanskelig å bruke stavemåten ble enstemmig uttrykt. Fremfor alt beskyldte imidlertid kritikerne Frege for å ignorere den algebraiske tilnærmingen i symbolsk logikk ( Ernst Schröder , Giuseppe Peano , George Boole , Augustus De Morgan , Charles Sanders Peirce ). Kritikken er berettiget: det merkes at Frege fullstendig ignorerer den dominerende strømmen av formell logikk og ikke forholder sitt eget arbeid til andre samtidige forskeres. Han kompenserte for denne utelatelsen i noen essays umiddelbart etter begrepet skriving .

Blant de få som tidlig anerkjente betydningen av den konseptuelle skrivingen, var den britiske filosofen og matematikeren Bertrand Russell , fenomenologen Edmund Husserl , Freges student Rudolf Carnap og den østerriksk-britiske filosofen Ludwig Wittgenstein , som skrev i forordet til sin berømte Tractatus logico-philosophicus (1921) skrev: "Alt jeg vil si er at jeg skylder mye av stimuleringen til tankene mine til de store verkene til Frege og verkene til min venn Mr. Bertrand Russell."

Det logistiske programmet, som den konseptuelle skrivingen bare var opptakten til, ble videreført spesielt av Russell og Alfred North Whitehead i deres monumentale Principia Mathematica (1910ff.), Som i noen tid ble ansett som det standard kanoniske arbeidet med logikk. Russell og Whitehead brukte allerede i hovedsak en av de logiske betegnelsene som ofte brukes i dag, den såkalte Peano-Russell- notasjonen, som er basert på staving av algebra .

Fra Freges symbolikk overlevde tegnet , kombinasjonen av dømmekraft og innholdslinje, (sannsynligvis gjennom formidling av Principia Mathematica ) , men mest i en generalisert betydning som en avledningsrelasjon . Videre kan negasjonstegnet som Arend Heyting introduserte i 1930 (opprinnelig for å skille den intuisjonistiske negatoren fra klassikeren) sees på som en innholdslinje med en negativ linje lagt til. ${\ displaystyle \ vdash}$ ${\ displaystyle \ neg}$

Selv om Freges egenartede stavemåte ikke var en stor suksess, er nesten alle verk i moderne logikk i det minste indirekte basert på den grunnleggende ideen til den konseptuelle skrivingen . Siden logikken også er hjelpe- og grunnleggende disiplin bl.a. matematikk, lingvistikk og informatikk, kan de indirekte effektene av Freges arbeid knapt overses. Innen helt ny fortid refererer anerkjente personligheter i filosofien gjentatte ganger til ideer fra begrepet manus , inkludert Michael Dummett og Robert Brandom .

Tabelloversikt over notasjonen

Freges notasjon	Moderne notasjon	Gjengivelse i daglig tale	betegnelse
	ingen direkte ekvivalent; en likhet i: ${\ displaystyle \ emptyset \ vdash A}$ ${\ displaystyle \ vdash A}$	i Frege og Russell: A er et faktum moderne: A er bevisbart	Likhet i moderne notasjon: avledning
	${\ displaystyle \ lnot A}$	A er ikke tilfelle for ikke-A	negasjon
	${\ displaystyle B \ til A}$	Hvis B, så A	Implikasjon, betinget, underkastelse
	${\ displaystyle A \ land B}$ ${\ displaystyle \ neg (B \ til \ neg A)}$	A og B	sammenheng
	${\ displaystyle A \ lor B}$ ${\ displaystyle \ neg B \ til A}$	a eller B	Disjunksjon, tillegg
	${\ displaystyle A \ leftrightarrow B}$ ${\ displaystyle A \, = \, B}$	A hvis og bare hvis B A er lik B.	Ekvivalens, bisubjunksjon; identitet
	${\ displaystyle \ forall xF (x)}$	Alt er F	Universell kvantifisering, universell kvantifisering
	${\ displaystyle \ lnot \ eksisterer xF (x)}$ ${\ displaystyle \ forall x \ lnot F (x)}$	Ingenting er F Det er ingen F
	${\ displaystyle \ eksisterer xF (x)}$ ${\ displaystyle \ lnot \ forall x \ lnot F (x)}$	Det er en F Minst en x er F	Eksistensiell kvantifisering, særlig kvantifisering
	${\ displaystyle \ forall x (G (x) \ til F (x))}$	Alle G er F
	${\ displaystyle \ eksisterer x (G (x) \ land F (x))}$ ${\ displaystyle \ lnot \ forall x (G (x) \ to \ lnot F (x))}$	Noen G er F Minst en G er F
	${\ displaystyle \ lnot \ eksisterer x (G (x) \ land F (x))}$ ${\ displaystyle \ forall x (G (x) \ to \ lnot F (x))}$	Nei G er F Alle G er ikke F
	${\ displaystyle \ eksisterer x (G (x) \ land \ lnot F (x))}$ ${\ displaystyle \ lnot \ forall x (G (x) \ til F (x))}$	Noen G er ikke F Ikke alle G er F

utgifter

• Konseptuell skriving. En av det aritmetiske simulerte formelspråket for ren tenkning. Halle 1879. [Originalutgave]
• Konseptuell skriving og andre essays, redigert av Ignacio Angelelli, Hildesheim 1964 u.ö. ISBN 978-3-487-00623-9
  [Denne opplagsutgaven har noen små, men noen ganger forstyrrende trykkfeil; spesielt mangler dommerlinjen på s. 1. Se notatet av Angelelli / Bynum i litteraturlisten.]

litteratur

• Ignacio Angelelli, Terrell Ward Bynum: Merknad om Freges konseptuelle skriving . I: Notre Dame Journal of Formal Logic . 7, nr. 4, 1966, s. 369-370. ISSN  0029-4527 . doi : 10.1305 / ndjfl / 1093958759 . (I hovedsak en liste over rettelser til opplagsutgaven av den konseptuelle forfatteren av Angelelli.)
• Franz Bolck (red.): Konseptuell skriving. Jena Frege-konferanse: 7. - 11. Mai 1979. Jena 1979.
• George Boolos: Les konseptuell skriving . I: Min . XCIV, nr. 375, 1985, s. 331-344. ISSN  0026-4423 . doi : 10.1093 / mind / XCIV.375.331 . Gjengitt på: ders.: Logic, Logic, and Logic , Cambridge (Mass.) 1998, 202-219. ISBN 978-0-674-53767-5 .
• John P. Burgess: On a Consistent Subsystem of Frege's Basic Laws . I: Notre Dame Journal of Formal Logic . 39, nr. 2, 1998, s. 274-278. doi : 10.1305 / ndjfl / 1039293068 .
• Gottlob Frege: Anvendelser av den konseptuelle skrivingen. Foredrag holdt på møtet 24. januar 1879 av Jena Society for Medicine and Science. I: Jenaische Zeitschrift für Naturwissenschaft 13 / Supplement II (1879) (møterapporter fra Jenaische Gesellschaft für Medizin und Naturwissenschaft for året 1879), 29–33. (Inkludert i opplagsutgaven av I. Angelelli.)
• Gottlob Frege: Om den vitenskapelige begrunnelsen for en konseptuell skriving. I: Tidsskrift for filosofi og filosofisk kritikk 81 (1882), 48–56. (Inkludert i opplagsutgaven av I. Angelelli.)
• Takk Gud Frege: Om formålet med den konseptuelle skrivingen. I: Jenaische Zeitschrift für Naturwissenschaft 16 (1883) Supplement, 1–10. (Inkludert i opplagsutgaven av I. Angelelli.)
• Takk Gud Frege: Boolsk logisk formelspråk og min konseptuelle skriving. I: ders.: Nachgelassene Schriften , 53–59.
• Gottlob Frege: Boolsk datalogikk og konseptuell skriving. I: ders.: Nachgelassene Schriften , 9–52.
• Takk Gud Frege: funksjon og konsept. (Foredrag holdt på møtet 9. januar 1891 i Jena Society for Medicine and Science. Håndgripelig i dette: Funksjon, konsept, mening .)
• Gottlob Frege: Nachged Schriften , redigert av Hans Hermes, Friedrich Kambartel og Friedrich Kaulbach, Hamburg 1969; utvidet andre utgave 1983. ISBN 978-3-7873-0490-5 .
• Takk Gud Frege: funksjon, konsept, mening. Fem logiske studier , redigert av G. Patzig, Göttingen 1994 u.ö. ISBN 978-3-525-33377-8 .
• JJ Green, Marcus Rossberg, Philip A. Ebert: Convenience of the Typesetter. Notasjon og typografi i Freges "Fundamental Laws of Arithmetic" . I: Bulletin of Symbolic Logic . 21, nr. 1, mai 2015, s. 15-30. (Beskriver den konseptuelle notasjonen av de grunnleggende lovene .)
• Otfried Höffe: Liten filosofihistorie , München 2008. ISBN 978-3-406-57385-9 .
• Tapio Korte: Freges konseptuelle skriving som en lingua characteristica . I: Syntese . 174, nr. 2, 2010, s. 283-294. doi : 10.1007 / s11229-008-9422-7 .
• Franz von Kutschera : Takk Gud Frege. En introduksjon til hans arbeid , Berlin / New York 1989. ISBN 978-3-11-012129-2 .
• Danielle Macbeth: Freges Logic , Cambridge (Mass.) 2005. ISBN 978-0-674-01707-8 .
• Richard L. Mendelsohn: The Philosophy of Gottlob Frege , Cambridge 2005. ISBN 978-0-521-83669-2 .
• Terence Parsons: På konsistensen av første ordens del av Freges logiske system . I: Notre Dame Journal of Formal Logic . 28, nr. 1, 1987, s. 161-168. doi : 10.1305 / ndjfl / 1093636853 .
• Ernst Schröder: Annonse fra Freges termskriving . I: Tidsskrift for matematikk og fysikk 25 (1881), 81–94.
• Hans Sluga: Frege mot booleanerne . I: Notre Dame Journal of Formal Logic . 28, nr. 1, 1987, s. 80-98. doi : 10.1305 / ndjfl / 1093636848 .
• John Venn: En gjennomgang av Freges konseptuelle skriving . I: Mind 5 (1880), 297.
• Risto Vilkko: Resepsjonen av Freges konseptuelle forfatterskap . I: Historia Mathematica . 25, nr. 4, november 1998, s. 412-422. ISSN  0315-0860 . doi : 10.1006 / hmat.1998.2213 . (Inneholder en oversikt over moderne mottakelse.)
• Matthias Wille: Gottlob Frege: Konseptuell skriving, en av det aritmetiske simulerte formelspråket for ren tenking. Berlin, Springer Spectrum, 2018 (Classical Science Texts), ISBN 978-3-662-45011-6 .
• Michael Wolff : Freges kritikk av den kantianske dommetabellen i hans 'concept writing' fra 1879. I: Michael Wolff: Fullstendigheten av den kantianske dommens tabell. Med et essay om Freges 'konseptuelle skriving'. Klostermann, Frankfurt 1995. ISBN 3-465-02811-2 , s. 243-312.
• Michael Wolff: Frege og det tradisjonelle syllogistikkbildet. I: Rüdiger Bubner og Gunnar Hindrichs (red.): Fra logikk til språk. Klett-Cotta, Stuttgart 2007, ISBN 978-3-608-94448-8 . Pp. 272-285.

weblenker

Wiktionary: Terminology  - forklaringer av betydninger, ordets opprinnelse, synonymer, oversettelser

• Edward N. Zalta:  Freges teorem og grunnlag for aritmetikk. I: Edward N. Zalta (red.): Stanford Encyclopedia of Philosophy .
• Begrepet skript i digital form for nedlasting
• En illustrasjon av det logiske systemet for konseptuell skriving av Stanley N. Burris (på engelsk)
• En kort introduksjon til Gottlob Freges konseptforfatterskap av Sven-Ake Wegner (Bergische Universität Wuppertal)
• Et interaktivt program for å konvertere proposisjonsuttrykk til konseptuell notasjon (og andre notasjoner) av Christian Gottschall

Individuelle bevis

1. ↑ Höffe: Kort filosofihistorie. S. 318.
2. ^ Jfr Sluga: "Frigjør mot booleanerne"
3. ↑ Se Volker Peckhaus: Logic, Mathesis universalis and general science , Berlin 1997. ISBN 978-3-05-003111-8
4. ↑ Jf. Tapio Korte: "Frege's concept writing as a lingua characteristica".
5. ↑ En ekstremt kritisk skisse av betraktningene om et slikt universelt språk, finnes i artikkelen "Universal Language" i: Fritz Mauthner: Dictionary of Philosophy , andre, utvidede utgave, Leipzig 1923. (online)
6. F Jf. Artikkelen “Characteristica universalis” i: Friedrich Kirchner / Carl Michaëlis: Dictionary of Basic Philosophical Concepts, 5. utgave Leipzig 1907, 116–117. (på nett)
7. ^ Adolf Trendelenburg: "Om Leibniz utkast til et generelt kjennetegn," i: Filosofiske avhandlinger fra Royal Academy of Sciences i Berlin fra året 1856, Berlin 1857, 36–69; Gjengitt på: ders.: Historical Contributions to Philosophy, Vol. 3: Vermischte Abhandlungen , Berlin 1867, 48–62.
8. ↑ ^{a b} Vilkko: "Mottakelsen av Freges logiske symbolikk ".
9. ↑ Se f.eks. B. søkeordet "ideografi" i Brockhaus 'Kleinem Konversations-Lexikon , 5. utgave 1911. (online)
10. ↑ Se også Frege: Funksjon og konsept .
11. ↑ ^{a b} Frege: Terminalsschrift , s.5.
12. ↑ Frege: Terminalsschrift , s. 24.
13. ↑ Se redaktørens fotnote i opplagsutgaven, s. 24.
14. ↑ En transkripsjon av de andre setningene i moderne notasjon finner du i vedlegget av Richard L. Mendelsohn: The Philosophy of Gottlob Frege .
15. ↑ Frege: Terminalsschrift , s.26.
16. ↑ Frege kjente dette prinsippet fra Leibniz-papiret Non inelegans specimen demonstrandi in abstractis publisert i 1840 og siterte det senere i sin Fundamentals of Arithmetic (1884) i §65: "Eadem sunt, quorum unam potest substiti alteri salva veritate."
17. ↑ Frege: Wortsschrift , s. 21. Jf. Kutschera: Gottlob Frege , s. 33f.
18. Utsch Kutschera: Gottlob Frege , s. 34.
19. ^ Parsons: På konsistensen av førsteordensdelen av Freges logiske system .
20. Ess Burgess: On a Consistent Subsystem of Frege's Basic Laws .
21. ↑ Jfr Kutschera: Gottlob Frege , kap. 6-8.
22. ↑ En detaljert diskusjon finner du i Richard G. Heck: "A Note on the Major Results of Terminology"
23. ↑ Frege: Wortsschrift , s. 61f., Setning 76.
24. ↑ Sluga: "Frege against the Booleans", s. 80.
25. ↑ Disse essayene er kun publisert i Nachlassen Schriften .
26. ↑ Ludwig Wittgenstein: Tractatus logico-philosophicus , forord. Sitert fra den kritiske utgaven av Brian McGuinness og Joachim Schulte, Frankfurt am Main 1989. ISBN 978-3-518-28959-4 .
27. ↑ Stephen C. Kleene: Introduction to Metamathematics , Amsterdam et al. 1952 og annet ISBN 978-0-7204-2103-3
28. ↑ Arend Heyting: "The formal rules of intuitionist logic," i: sesjonsrapporter fra det preussiske vitenskapsakademiet, fys.-matematikk. Klasse , 1930, s. 42-65.

	Denne artikkelen er tilgjengelig som en lydfil:
	Lagre | Informasjon  | 14:39 min (8,44 MB) Tekst til den talte versjonen
	Mer informasjon på talt Wikipedia

Denne versjonen ble lagt til i listen over artikler som er verdt å lese 9. september 2007 .