Taylor formel

The Taylor formel (også Taylor teorem ) er et resultat fra den matematiske gren av analyse . Den er oppkalt etter matematikeren Brook Taylor . Denne formelen kan brukes til å tilnærme funksjoner i nærheten av et punkt ved hjelp av polynomer , de såkalte Taylor polynomene . Man snakker også om Taylor-tilnærmingen . Taylor-formelen er et verktøy innen mange ingeniør- , samfunns- og naturvitenskap på grunn av dens relativt enkle anvendelighet og brukbarhetbli til. Et komplisert analytisk uttrykk kan tilnærmes med et Taylor-polynom av lav grad (ofte bra), f.eks. B. i fysikk eller i justering av geodetiske nettverk. Den ofte brukte tilnærmingen med liten vinkel på sinusen er en Taylor-serie av denne funksjonen som blir brutt av etter første periode.

Nært knyttet til Taylor-formelen er den såkalte Taylor-serien (Taylor- utvidelse ).

motivasjon

Tilnærming ved tangens

En tilnærming for en differensierbar funksjon ved et punkt med en rett linje , dvs. av et polynom av 1. grad, er gitt av tangenten til ligningen ${\ displaystyle f}$${\ displaystyle a}$

${\ displaystyle T_ {1} f (x; a) = f (a) + f '(a) (xa)}$.

Den kan kjennetegnes ved at det ved plassering av funksjonsverdiene og verdiene av den første deriverte (= helling) til og kamp: . ${\ displaystyle x = a}$${\ displaystyle f (x)}$${\ displaystyle T_ {1} f (x; a)}$${\ displaystyle f (a) = T_ {1} f (a; a), f '(a) = T_ {1}' f (a; a)}$

Hvis du definerer resten , så holder det . Funksjonen tilnærmet nær punktet i den forstand som holder for resten ${\ displaystyle R_ {1} f (x; a): = f (x) -T_ {1} f (x; a)}$${\ displaystyle f (x) = T_ {1} f (x; a) + R_ {1} f (x; a)}$${\ displaystyle T_ {1} f (x; a)}$${\ displaystyle f}$${\ displaystyle x = a}$

${\ displaystyle (1) ~ \ lim _ {x \ to a} {\ frac {R_ {1} f (x; a)} {xa}} = \ lim _ {x \ to a} {\ frac {f (x) -T_ {1} f (x; a)} {xa}} = \ lim _ {x \ til a} {\ frac {f (x) -f (a)} {xa}} - f ' (a) = 0}$(se definisjonen av derivatet ).

Tilnærming ved hjelp av en osculerende lignelse

Man kan anta at man får en enda bedre tilnærming for noe som er to ganger differensierbart hvis man bruker et kvadratisk polynom , som man krever som også stemmer. De tilnærming fører ved å beregne derivater på og , så ${\ displaystyle f}$ ${\ displaystyle T_ {2} f (x; a)}$${\ displaystyle T_ {2} '' f (a; a) = f '' (a)}$ ${\ displaystyle T_ {2} f (x; a) = a_ {0} + a_ {1} (xa) + a_ {2} (xa) ^ {2}}$${\ displaystyle a_ {0} = f (a), a_ {1} = f '(a)}$${\ displaystyle a_ {2} = {\ frac {1} {2}} f '' (a)}$

${\ displaystyle T_ {2} f (x; a) = f (a) + f '(a) (xa) + {\ frac {1} {2}} f' '(a) (xa) ^ {2 }}$.

Denne tilnærmingsfunksjonen er også kjent som en osculerende parabel.

Du definerer nå riktig rest , slik at igjen . Da får vi at den osculerende parabolen faktisk tilnærmer den gitte funksjonen bedre fordi nå (med regelen i de l'Hospital ): ${\ displaystyle R_ {2} f (x; a): = f (x) -T_ {2} f (x; a)}$${\ displaystyle f (x) = T_ {2} f (x; a) + R_ {2} f (x; a)}$${\ displaystyle x = a}$

${\ displaystyle \ lim _ {x \ to a} {\ frac {R_ {2} f (x; a)} {(xa) ^ {2}}} = \ lim _ {x \ to a} {\ frac {f (x) -f (a) -f '(a) (xa)} {(xa) ^ {2}}} - {\ frac {1} {2}} f' '(a) = \ lim _ {x \ to a} {\ frac {f '(x) -f' (a)} {2 (xa)}} - {\ frac {1} {2}} f '' (a) = 0}$

gjelder.

Tilnærming av polynomer av grad n

Denne prosedyren kan nå lett generaliseres til polynomier- th grad : Her skal gjelde ${\ displaystyle n}$${\ displaystyle T_ {n} (x)}$

${\ displaystyle T_ {n} f (a; a) = f (a), \ T_ {n} 'f (a; a) = f' (a), \ \ ldots, \ T_ {n} ^ {( n)} f (a; a) = f ^ {(n)} (a)}$.

Det gir seg

${\ displaystyle T_ {n} f (x; a) = f (a) + {\ frac {f '(a)} {1!}} (xa) + {\ frac {f' '(a)} { 2!}} (Xa) ^ {2} + \ dotsb + {\ frac {f ^ {(n)} (a)} {n!}} (Xa) ^ {n}}$.

Med de l'Hospitals regel finner vi også:

${\ displaystyle \ lim _ {x \ to a} {\ frac {f (x) -T_ {n} f (x; a)} {(xa) ^ {n}}} = \ lim _ {x \ to a} {\ frac {f '(x) -T_ {n}' f (x; a)} {n (xa) ^ {n-1}}}}$.

Derav med full induksjon på det følger at for : ${\ displaystyle n}$${\ displaystyle R_ {n} f (x; a) = f (x) -T_ {n} f (x; a)}$

${\ displaystyle \ lim _ {x \ to a} {\ frac {R_ {n} f (x; a)} {(xa) ^ {n}}} = 0}$.

Kvalitativ Taylor-formel

Hvis -mal er forskjellig, følger det umiddelbart av ovenstående hensyn at ${\ displaystyle f}$ ${\ displaystyle n}$

${\ displaystyle f (x) = T_ {n} f (x; a) + R_ {n} f (x; a) = T_ {n} f (x; a) + o (| xa | ^ {n} ), \ quad x \ rightarrow a,}$

hvor står for Landau-notasjonen . Denne formelen kalles den ”kvalitative Taylor-formelen”. ${\ displaystyle o}$

Jo nærmere inn , jo bedre så tilnærmet (den såkalte Taylor polynom, se nedenfor ) på punktet funksjonen . ${\ displaystyle x}$${\ displaystyle a}$${\ displaystyle T_ {n} f (x; a)}$${\ displaystyle x}$${\ displaystyle f}$

Definisjoner og teorem

I det følgende presenteres Taylor-formelen med integrert rest. Taylor-formelen finnes også i varianter med en annen restbetegnelse; imidlertid følger disse formlene fra Taylor-formelen med en integrert restbetegnelse. De er i delen Resten av formler nedenfor .

La være et intervall og en -time kontinuerlig differensierbar funksjon . I de følgende formlene står for den første, andre, ..., -derivat av funksjonen . ${\ displaystyle I \ subset \ mathbb {R}}$${\ displaystyle f \ colon I \ to \ mathbb {R}}$${\ displaystyle (n + 1)}$ ${\ displaystyle f ', f' ', \ dots, f ^ {(k)}}$${\ displaystyle k}$${\ displaystyle f}$

Taylor polynom

Den -te Taylor polynom på utviklingen punkt er definert ved: ${\ displaystyle n}$${\ displaystyle a \ i I}$

${\ displaystyle {\ begin {align} T_ {n} f (x; a) = & \ sum _ {k = 0} ^ {n} {f ^ {(k)} (a) \ over k!} ( xa) ^ {k} \\ = & f (a) + {\ frac {f '(a)} {1!}} (xa) + {\ frac {f' '(a)} {2!}} (xa) ^ {2} + \ ldots + {\ frac {f ^ {(n)} (a)} {n!}} (xa) ^ {n} \ end {justert}}}$

Integrert rest

Den tredje integrerte resten er definert av: ${\ displaystyle n}$

${\ displaystyle R_ {n} f (x; a) = \ int \ limits _ {a} ^ {x} {\ frac {(xt) ^ {n}} {n!}} f ^ {(n + 1 )} (t) \, \ mathrm {d} t}$

Teorem (Taylor-formel med integrert restbetegnelse)

Følgende gjelder for alle og fra : ${\ displaystyle a}$${\ displaystyle x}$${\ displaystyle I}$

${\ displaystyle {\ begin {align} f (x) = & T_ {n} f (x; a) + R_ {n} f (x; a) \\ = & \ sum _ {k = 0} ^ { n} {f ^ {(k)} (a) \ over k!} (xa) ^ {k} + \ int \ limits _ {a} ^ {x} {\ frac {(xt) ^ {n}} {n!}} f ^ {(n + 1)} (t) \, \ mathrm {d} t \ end {justert}}}$

bevis

Beviset på Taylor-formelen med integrert resten gjøres ved induksjon over . ${\ displaystyle n}$

Induksjonsstarten tilsvarer nøyaktig den grunnleggende analysesetningen , brukt på den en gang kontinuerlig differensierbare funksjonen : ${\ displaystyle n = 0}$${\ displaystyle f}$

${\ displaystyle f (x) = f (a) + \ int \ limits _ {a} ^ {x} f '(t) \, \ mathrm {d} t = T_ {0} f (x; a) + R_ {0} f (x; a)}$

Induksjonstrinnet (det må vises at formelen alltid holder, hvis den holder i a ) skjer gjennom delvis integrering . For noe som kontinuerlig kan differensieres, får vi: ${\ displaystyle n \ rightarrow n + 1}$${\ displaystyle n + 1}$${\ displaystyle n}$${\ displaystyle (n + 2)}$${\ displaystyle f}$

${\ displaystyle {\ begin {align} & {\ frac {f ^ {(n + 1)} (a)} {(n + 1)!}} (xa) ^ {n + 1} + R_ {n + 1} f (x; a) \\ = & {\ frac {f ^ {(n + 1)} (a)} {(n + 1)!}} (Xa) ^ {n + 1} + \ int \ begrenser _ {a} ^ {x} {\ frac {(xt) ^ {n + 1}} {(n + 1)!}} f ^ {(n + 2)} (t) \, \ mathrm { d} t \\ = & {\ frac {f ^ {(n + 1)} (a)} {(n + 1)!}} (xa) ^ {n + 1} + \ left [{\ frac { (xt) ^ {n + 1}} {(n + 1)!}} f ^ {(n + 1)} (t) \ høyre] _ {t = a} ^ {t = x} - \ int \ begrenser _ {a} ^ {x} {\ frac {- (xt) ^ {n}} {n!}} f ^ {(n + 1)} (t) \, \ mathrm {d} t \\ = & {\ frac {(xa) ^ {n + 1}} {(n + 1)!}} f ^ {(n + 1)} (a) - {\ frac {(xa) ^ {n + 1} } {(n + 1)!}} f ^ {(n + 1)} (a) + R_ {n} f (x; a) \\ = & R_ {n} f (x; a) \ end { justert}}}$

og dermed

${\ displaystyle T_ {n + 1} f (x; a) + R_ {n + 1} f (x; a) = T_ {n} f (x; a) + R_ {n} f (x; a) = f (x)}$.

Resten av formler

I tillegg til den integrerte formelen, er det andre representasjoner av resten av begrepet.

Schlömilch gjenværende kobling og dens avledning

I henhold til gjennomsnittsverdisetningen til integral kalkulus følger det for hvert naturlige tall med at det er et mellom og , slik at: ${\ displaystyle p}$${\ displaystyle 1 \ leq p \ leq n + 1}$${\ displaystyle \ xi}$${\ displaystyle a}$${\ displaystyle x}$

${\ displaystyle \ int \ limit _ {a} ^ {x} {f ^ {(n + 1)} (t) {\ frac {(xt) ^ {n + 1-p}} {n!}} \ cdot (xt) ^ {p-1} \, \ mathrm {d} t} = {\ frac {f ^ {(n + 1)} (\ xi) (x- \ xi) ^ {n + 1-p }} {n!}} \ cdot \ underbrace {\ int \ limits _ {a} ^ {x} {(xt) ^ {p-1} \, \ mathrm {d} t}} _ {= {\ frac {(xa) ^ {p}} {p}}}}$

Dette følger Schlömilch gjenværende lemform :

${\ displaystyle R_ {n} f (x; a) = \ int \ limits _ {a} ^ {x} {\ frac {(xt) ^ {n}} {n!}} f ^ {(n + 1 )} (t) \, \ mathrm {d} t = {\ frac {f ^ {(n + 1)} (\ xi)} {p \ cdot n!}} (x- \ xi) ^ {n + 1-p} (xa) ^ {p}}$

for en mellom og . ${\ displaystyle \ xi}$${\ displaystyle a}$${\ displaystyle x}$

Spesielle tilfeller av Schlömilch gjenværende lem

Et spesielt tilfelle, nemlig det med , er Cauchy-formen : ${\ displaystyle p = 1}$

${\ displaystyle R_ {n} f (x; a) = {\ frac {f ^ {(n + 1)} (\ xi)} {n!}} (x- \ xi) ^ {n} (xa) }$

for en mellom og . ${\ displaystyle \ xi}$${\ displaystyle a}$${\ displaystyle x}$

I det spesielle tilfellet får vi den Lagrangiske resten : ${\ displaystyle p = n + 1}$

${\ displaystyle R_ {n} f (x; a) = {\ frac {f ^ {(n + 1)} (\ xi)} {(n + 1)!}} (xa) ^ {n + 1} }$

for en mellom og . I denne representasjonen trenger ikke det tredje derivatet være kontinuerlig. ${\ displaystyle \ xi}$${\ displaystyle a}$${\ displaystyle x}$${\ displaystyle (n + 1)}$${\ displaystyle f}$

Peano gjenværende kobling

Ved å bruke Taylor-formelen med en Lagrange-rest, oppnår man også for -mal kontinuerlig differensierbar : ${\ displaystyle n}$${\ displaystyle f}$

${\ displaystyle f (x) = T_ {n-1} f (x; a) + {\ frac {f ^ {(n)} (\ xi)} {n!}} (xa) ^ {n} = T_ {n} f (x; a) + {\ frac {f ^ {(n)} (\ xi) -f ^ {(n)} (a)} {n!}} (Xa) ^ {n} }$

Det er derfor du kan som en resten

${\ displaystyle R_ {n} f (x; a) = {\ frac {f ^ {(n)} (\ xi) -f ^ {(n)} (a)} {n!}} (xa) ^ {n}}$

bruk, med bare tider må være kontinuerlig forskjellig. Denne resten kalles en Peano-rest . ${\ displaystyle f}$${\ displaystyle n}$

Videre representasjon

Hvis man setter , det vil si at den lagrangiske representasjonen mottar skjemaet ${\ displaystyle \ Theta = {\ tfrac {\ xi -a} {xa}}}$${\ displaystyle \ xi = a + \ Theta (xa)}$

${\ displaystyle R_ {n} f (x; a) = {\ frac {f ^ {(n + 1)} (a + \ Theta (xa))} {(n + 1)!}} (xa) ^ {n + 1}}$,

Schlömilchsche

${\ displaystyle R_ {n} f (x; a) = {\ frac {f ^ {(n + 1)} (a + \ Theta (xa))} {p \ cdot n!}} (1- \ Theta ) ^ {n + 1-p} (xa) ^ {n + 1}}$,

og Cauchysche

${\ displaystyle R_ {n} f (x; a) = {\ frac {f ^ {(n + 1)} (a + \ Theta (xa))} {n!}} (1- \ Theta) ^ { n} (xa) ^ {n + 1}}$

hver for en mellom 0 og 1. ${\ displaystyle \ Theta}$

Resttidsestimat

Hvis intervallet ligger i (domenet til ), kan man utlede følgende estimat med resten av Lagrange (se i avsnittet resten formler ) for alle og på grunn av mellom og (og dermed også ): ${\ displaystyle (ar, a + r)}$${\ displaystyle I}$${\ displaystyle f}$${\ displaystyle x \ in (ar, a + r)}$${\ displaystyle \ xi}$${\ displaystyle a}$${\ displaystyle x}$${\ displaystyle \ xi \ in (ar, a + r)}$

${\ displaystyle | R_ {n} f (x; a) | = \ left | {\ frac {f ^ {(n + 1)} (\ xi)} {(n + 1)!}} (xa) ^ {n + 1} \ høyre | \ leq \ sup _ {\ xi \ in (ar, a + r)} \ venstre | {\ frac {f ^ {(n + 1)} (\ xi)} {(n +1)!}} (Xa) ^ {n + 1} \ høyre |}$

Hvis det gjelder alle , gjelder estimatet for resten av begrepet ${\ displaystyle | f ^ {(n + 1)} (x) | \ leq M_ {n}}$${\ displaystyle x \ in (ar, a + r)}$

${\ displaystyle \ forall x \ in (ar, a + r): | R_ {n} f (x; a) | \ leq M_ {n} {\ frac {| xa | ^ {n + 1}} {( n + 1)!}} \ leq M_ {n} {\ frac {r ^ {n + 1}} {(n + 1)!}}}$.

Tilnærmingsformler for sinus og cosinus

En anvendelse av Taylor-formelen er tilnærmelsesformler, presentert her ved hjelp av eksemplet på sinus og cosinus (der argumentet er gitt i radianer ).

For , det fjerde Taylor polynom av sinusfunksjonen ved ekspansjonspunktet er 0 ${\ displaystyle f (x) = \ sin (x)}$${\ displaystyle f '(x) = \ cos (x), \, f' '(x) = - \ sin (x), \, f' '' (x) = - \ cos (x), f ' '' '(x) = \ sin (x)}$

${\ displaystyle T_ {4} \ sin (x; 0) = f (0) + f '(0) x + {\ frac {1} {2}} f' '(0) x ^ {2} + { \ frac {1} {6}} f '' '(0) x ^ {3} + {\ frac {1} {24}} f' '' '(0) x ^ {4} = x - {\ frac {x ^ {3}} {6}}.}$

Fra resultater for resten av Lagrange med mellom 0 og . På grunn av resten av begrepet følger . ${\ displaystyle f ^ {(5)} (x) = \ cos (x)}$${\ displaystyle R_ {4} \ sin (x; 0) = {\ frac {f ^ {(5)} (\ xi)} {5!}} x ^ {5} = {\ frac {\ cos (\ xi)} {120}} x ^ {5}}$${\ displaystyle \ xi}$${\ displaystyle x}$${\ displaystyle | {\ cos (\ xi)} | \ leq 1}$${\ displaystyle | T_ {4} \ sin (x; 0) - \ sin (x) | \ leq {\ frac {| x | ^ {5}} {120}}}$

Hvis det er mellom og , er det relative avviket fra til mindre enn 0,5%. ${\ displaystyle x}$${\ displaystyle - {\ frac {\ pi} {4}}}$${\ displaystyle {\ frac {\ pi} {4}}}$${\ displaystyle \ left | {\ frac {T_ {4} \ sin (x; 0) - \ sin (x)} {\ sin (x)}} \ right |}$${\ displaystyle T_ {3} \ sin (x; 0)}$${\ displaystyle \ sin (x)}$

Faktisk er tredje ordens Taylor polynom tilstrekkelig for å tilnærme sinus til denne nøyaktigheten, siden for , og derfor . Dette resulterer også i følgende ytterligere estimat for det tredje og fjerde Taylor-polynomet, som er mer presist for veldig store x: ${\ displaystyle f '' '' (0) = 0}$${\ displaystyle f (x) = \ sin (x)}$${\ displaystyle T_ {3} \ sin (x; 0) = T_ {4} \ sin (x; 0)}$

${\ displaystyle | T_ {4} \ sin (x; 0) - \ sin (x) | \ leq {\ frac {x ^ {4}} {24}}}$

Følgende figur viser grafene til noen Taylor polynomer av sinus rundt utviklingspunkt 0 for . Grafen tilhører Taylor-serien , som tilsvarer sinusfunksjonen. ${\ displaystyle n = 1,3,5,15}$${\ displaystyle n = \ infty}$

Tilnærming av sinus av Taylor polynomer opp til${\ displaystyle T_ {1} \ sin (x; 0)}$${\ displaystyle T_ {81} \ sin (x; 0)}$

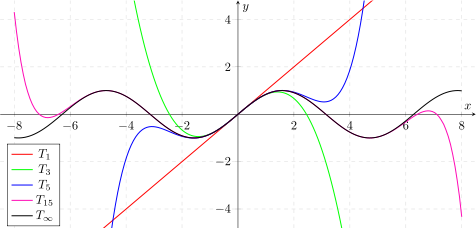
Det fjerde Taylor-polynomet til cosinusfunksjonen ved ekspansjonspunktet 0 har denne formen i Horner-skjemaet : ${\ displaystyle T_ {4} \ cos (x; 0)}$

${\ displaystyle \ cos (x) \ approx T_ {4} \ cos (x; 0) = \ left ({\ frac {x ^ {2}} {12}} - 1 \ right) \ cdot {\ frac { x ^ {2}} {2}} + 1}$

Hvis x er mellom og , er den relative avviket mindre enn 0,05%. ${\ displaystyle - {\ frac {\ pi} {4}}}$${\ displaystyle {\ frac {\ pi} {4}}}$${\ displaystyle \ left | {\ frac {T_ {4} \ cos (x; 0) - \ cos (x)} {\ cos (x)}} \ right |}$

Du kan også bruke disse formlene for cotangens og tangens , fordi det er det

${\ displaystyle \ tan (x) \ sim t (x) = {\ frac {T_ {3} \ sin (x; 0)} {T_ {4} \ cos (x; 0)}}}$

med et relativt avvik på mindre enn 0,5% for , og med samme relative avvik (det er ikke noe Taylor-polynom av tangenten). ${\ displaystyle \ left | x \ right | <{\ frac {\ pi} {4}}}$${\ displaystyle \ cot (x) \ sim 1 / t (x)}$${\ displaystyle t}$

Hvis du trenger enda høyere nøyaktighet for tilnærmelsesformlene, kan du falle tilbake på høyere Taylor-polynomer, som tilnærmer funksjonene enda bedre.

Taylor-formel i flerdimensjonalt

La oss i det følgende være en kontinuerlig differensierbar funksjon og . Er videre , hvor . ${\ displaystyle f \ colon \ mathbb {R} ^ {d} \ to \ mathbb {R}}$${\ displaystyle n + 1}$${\ displaystyle x = (x_ {1}, \ ldots, x_ {d}), a = (a_ {1}, \ ldots, a_ {d}) \ in \ mathbb {R} ^ {d}}$${\ displaystyle F \ colon \ mathbb {R} \ to \ mathbb {R}}$${\ displaystyle F (t) = f (a + th)}$${\ displaystyle h = xa}$

Videre være som i flerindeksnotasjonen . I det følgende avsnitt, den multi-indeksen er notasjonen som brukes, slik at man umiddelbart kan se at den multi-dimensjonale tilfellet gir faktisk de samme formler for den en-dimensjonale tilfellet. ${\ displaystyle D ^ {\ alpha} = {\ frac {\ partial ^ {| \ alpha |}} {\ partial x_ {1} ^ {\ alpha _ {1}} \ cdots \ partial x_ {d} ^ { \ alpha _ {d}}}}$${\ displaystyle d = 1}$

Flerdimensjonalt Taylor polynom

Med den flerdimensjonale kjedelegelen og induksjonen oppnår man det

${\ displaystyle F ^ {(n)} (t) = \ sum _ {| \ alpha | = n} \ left ({\ begin {matrix} n \\\ alpha \ end {matrix}} \ right) (xa ) ^ {\ alpha} D ^ {\ alpha} f (a + th)}$,

hvor er den multinomiale koeffisienten , se også multinomial teorem . ${\ displaystyle \ left ({\ begin {matrix} n \\\ alpha \ end {matrix}} \ right)}$

Hvis man i punkt 1 representerer et Taylor-polynom med utviklingspunkt 0, gir denne formelen definisjonen av det flerdimensjonale Taylor-polynomet på utviklingspunktet : ${\ displaystyle F}$${\ displaystyle f}$${\ displaystyle a}$

${\ displaystyle T_ {n} f (x; a): = T_ {n} F (1; 0) = \ sum _ {| \ alpha | = 0} ^ {n} {\ frac {(xa) ^ { \ alpha}} {\ alpha!}} D ^ {\ alpha} f (a)}$

Her ble det brukt det . ${\ displaystyle \ left ({\ begin {matrix} n \\\ alpha \ end {matrix}} \ right) \ cdot {\ frac {1} {n!}} = {\ frac {1} {\ alpha! }}}$

Oscillerende firkant

Det andre Taylor-polynomet til en skalarverdig funksjon i mer enn en variabel kan skrives mer kompakt opp til andre rekkefølge enn:

${\ displaystyle T_ {2} f (x; a) = f (a) + \ nabla f (a) ^ {\ mathrm {T}} (xa) + {\ frac {1} {2}} (xa) ^ {\ mathrm {T}} \ operatorname {H} _ {f} (a) (xa)}$

Her er gradienten og den hessiske matrisen til hver på stedet . ${\ displaystyle \ nabla f (a)}$${\ displaystyle \ operatorname {H} _ {f} (a)}$${\ displaystyle f}$${\ displaystyle a}$

Det andre Taylor-polynomet kalles også en oscillerende firkant .

Flerdimensjonal integrert rest

Den flerdimensjonale resten av perioden er også definert ved hjelp av multi-indeks notasjon:

${\ displaystyle {\ begin {align} R_ {n} f (x; a): = & R_ {n} F (1; 0) = \ int \ limits _ {0} ^ {1} {\ frac {( 1 -t) ^ {n}} {n!}} F ^ {(n + 1)} (t) \, \ mathrm {d} t \\ = & (n + 1) \ int \ limits _ {0 } ^ {1} \ sum _ {| \ alpha | = n + 1} {\ frac {(1-t) ^ {n} (xa) ^ {\ alpha}} {\ alpha!}} D ^ {\ alfa} f (a + th) \, \ mathrm {d} t \ end {justert}}}$

Flerdimensjonal Taylor-formel

Fra den endimensjonale Taylor-formelen følger det

${\ displaystyle F (1) = T_ {n} F (1; 0) + R_ {n} F (1; 0)}$

Derfor, i henhold til definisjonen ovenfor , oppnår man: ${\ displaystyle F (t)}$

${\ displaystyle f (x) = T_ {n} f (x; a) + R_ {n} f (x; a)}$

Flerdimensjonale restformler

De endimensjonale ikke-integrerte restformlene kan også generaliseres for flerdimensjonalt tilfelle ved hjelp av formelen for . ${\ displaystyle F ^ {(n)} (t)}$

Schlömilch-resten blir slik

${\ displaystyle R_ {n} f (x; a) = {\ frac {(n + 1) (1- \ theta) ^ {n + 1-p}} {p}} \ sum _ {| \ alpha | = n + 1} {\ frac {(xa) ^ {\ alpha} D ^ {\ alpha} f (a + \ theta h)} {\ alpha!}}}$,

resten av det lagrangiske begrepet

${\ displaystyle R_ {n} f (x; a) = \ sum _ {| \ alpha | = n + 1} {\ frac {(xa) ^ {\ alpha} D ^ {\ alpha} f (a + \ theta h)} {\ alpha!}}}$,

og resten av Cauchy

${\ displaystyle R_ {n} f (x; a) = (n + 1) (1- \ theta) ^ {n} \ sum _ {| \ alpha | = n + 1} {\ frac {(xa) ^ {\ alpha} D ^ {\ alpha} f (a + \ theta h)} {\ alpha!}}}$

for hver enkelt . ${\ displaystyle \ theta \ in [0,1]}$

Kvalitativ Taylor-formel

I følge den flerdimensjonale Taylor-formelen med Lagrange-resten får vi:

${\ displaystyle f (x) -T_ {n + 1} f (x; a) = (n + 1) \ left (\ sum _ {| \ alpha | = n + 1} {\ frac {(xa) ^ {\ alpha} D ^ {\ alpha} f (a + \ theta h)} {\ alpha!}} - \ sum _ {| \ alpha | = n + 1} {\ frac {(xa) ^ {\ alpha } D ^ {\ alpha} f (a)} {\ alpha!}} \ Right)}$

På grunn av dette får vi også: ${\ displaystyle | x_ {i} -a_ {i} | \ leq \ | xa \ |}$

${\ displaystyle {\ begin {justert} & (n + 1) \ venstre | \ sum _ {| \ alpha | = n + 1} {\ frac {(xa) ^ {\ alpha} D ^ {\ alpha} f (a + \ theta h)} {\ alpha!}} - \ sum _ {| \ alpha | = n + 1} {\ frac {(xa) ^ {\ alpha} D ^ {\ alpha} f (a) } {\ alpha!}} \ right | \\\ leq & (n + 1) \ | xa \ | ^ {n + 1} \ cdot \ underbrace {\ left | \ sum _ {| \ alpha | = n + 1} {\ frac {D ^ {\ alpha} f (a + \ theta h) -D ^ {\ alpha} f (a)} {\ alpha!}} \ Right |} _ {\ to 0 {\ text {,}} x \ til a} \ end {justert}}}$

Den siste delen har en tendens mot null, siden gradens delvise derivater er kontinuerlige og ligger mellom og og dermed også konvergerer til, hvis . ${\ displaystyle n + 1}$${\ displaystyle a + \ theta h}$${\ displaystyle x}$${\ displaystyle a}$${\ displaystyle a}$${\ displaystyle x \ til a}$

Vi får følgende estimat, som kalles "(flerdimensjonal) kvalitativ Taylor-formel":

${\ displaystyle f (x) = T_ {n + 1} f (x; a) + {\ mathcal {O}} (\ | xa \ | ^ {n + 1})}$

for , hvor står for Landau-notasjon .${\ displaystyle x \ til a}$${\ displaystyle {\ mathcal {O}}}$

eksempel

Det skal fungere

${\ displaystyle f: \ {(x_ {1}, x_ {2}) \ in \ mathbb {R} ^ {2}, \ x_ {2} <1 \} \ to \ mathbb {R}, ~ (x_ {1}, x_ {2}) \ mapsto \ exp (x_ {1} -x_ {2}) \ cdot \ log (1-x_ {2})}$

som skal utvikles rundt poenget . ${\ displaystyle a = (a_ {1}, a_ {2}) = (1.0) \ in \ mathbb {R} ^ {2}}$

I dette eksemplet skal funksjonen utvikles opp til andre grad, det vil si en andre ordens Taylor polynom skal beregnes, den såkalte oscillation quadric . Så det gjelder . På grunn av behov, i henhold til den multi-indeksen notasjon , er tupler , , , , og blir tatt hensyn til. På grunn av Schwarz-teoremet holder den det ${\ displaystyle n = 2}$${\ displaystyle | \ alpha | \ leq n}$${\ displaystyle (0,0)}$${\ displaystyle (1,0)}$${\ displaystyle (0,1)}$${\ displaystyle (2.0)}$${\ displaystyle (1,1)}$${\ displaystyle (0.2)}$

${\ displaystyle {\ frac {\ partial ^ {2} f} {\ partial x_ {1} \ partial x_ {2}}} (a) = {\ frac {\ partial ^ {2} f} {\ partial x_ {2} \ partial x_ {1}}} (a)}$.

De partielle deriverte av den funksjon er:

${\ displaystyle {\ frac {\ partial f} {\ partial x_ {1}}} (a) = \ left [\ exp (x_ {1} -x_ {2}) \ cdot \ log (1-x_ {2 }) \ høyre] _ {x = (1,0)} = 0}$

${\ displaystyle {\ frac {\ partial f} {\ partial x_ {2}}} (a) = \ left [- \ exp (x_ {1} -x_ {2}) \ cdot \ left (\ log (1 -x_ {2}) + {\ frac {1} {1-x_ {2}}} \ høyre) \ høyre] _ {x = (1,0)} = - e}$

${\ displaystyle {\ frac {\ partial ^ {2} f} {\ partial x_ {1} ^ {2}}} (a) = \ left [\ exp (x_ {1} -x_ {2}) \ cdot \ log (1-x_ {2}) \ høyre] _ {x = (1,0)} = 0}$

${\ displaystyle {\ frac {\ partial ^ {2} f} {\ partial x_ {1} \ partial x_ {2}}} (a) = {\ frac {\ partial ^ {2} f} {\ partial x_ {2} \ partial x_ {1}}} (a) = \ left [- \ exp (x_ {1} -x_ {2}) \ cdot \ left (\ log (1-x_ {2}) + {\ frac {1} {1-x_ {2}}} \ høyre) \ høyre] _ {x = (1,0)} = - e}$

${\ displaystyle {\ frac {\ partial ^ {2} f} {\ partial x_ {2} ^ {2}}} (a) = \ left [\ exp (x_ {1} -x_ {2}) \ left (\ log (1-x_ {2}) + {\ frac {2} {1-x_ {2}}} - {\ frac {1} {(1-x_ {2}) ^ {2}}} \ høyre) \ høyre] _ {x = (1,0)} = e}$

Det følger med den flerdimensjonale Taylor-formelen:

${\ displaystyle {\ begin {align} f (x) \ approx & f (a) + {\ frac {1} {1!}} {\ frac {\ partial f} {\ partial x_ {1}}} ( a) ~ (x_ {1} -a_ {1}) + {\ frac {1} {1!}} {\ frac {\ partial f} {\ partial x_ {2}}} (a) ~ (x_ { 2} -a_ {2}) \\ & + {\ frac {1} {2!}} {\ Frac {\ partial ^ {2} f} {\ partial x_ {1} ^ {2}}} (a ) ~ (x_ {1} -a_ {1}) ^ {2} + {\ frac {1} {1! 1!}} {\ frac {\ partial ^ {2} f} {\ partial x_ {1} \ partial x_ {2}}} (a) ~ (x_ {1} -a_ {1}) (x_ {2} -a_ {2}) \\ & + {\ frac {1} {2!}} { \ frac {\ partial ^ {2} f} {\ partial x_ {2} ^ {2}}} (a) ~ (x_ {2} -a_ {2}) ^ {2} \\ & = 0 + 0 - e (x_ {2} -0) + 0-e (x_ {1} -1) (x_ {2} -0) + {\ frac {1} {2}} e (x_ {2} -0) ^ {2} \\ & = - ex_ {1} x_ {2} + {\ frac {1} {2}} ex_ {2} ^ {2} \ end {align}}}$

Hvis man bruker den alternative representasjonen ved hjelp av gradienten og den hessiske matrisen, får man:

${\ displaystyle {\ begin {justert} f (x) & \ ca f (a) + \ nabla f (a) ^ {T} (xa) + {\ frac {1} {2}} (xa) ^ { T} H_ {f} (a) (xa) \\ & = f (a) + {\ begin {pmatrix} {\ frac {\ partial f} {\ partial x_ {1}}} (a) & {\ frac {\ partial f} {\ partial x_ {2}}} (a) \ end {pmatrix}} {\ begin {pmatrix} x_ {1} -a_ {1} \\ x_ {2} -a_ {2} \ end {pmatrix}} \\ & \ qquad + {\ frac {1} {2}} {\ begin {pmatrix} x_ {1} -a_ {1} & x_ {2} -a_ {2} \ end { pmatrix}} {\ begin {pmatrix} {\ frac {\ partial ^ {2} f} {\ partial x_ {1} ^ {2}}} (a) & {\ frac {\ partial ^ {2} f} {\ partial x_ {2} \ partial x_ {1}}} (a) \\ {\ frac {\ partial ^ {2} f} {\ partial x_ {1} \ partial x_ {2}}} (a) & {\ frac {\ partial ^ {2} f} {\ partial x_ {2} ^ {2}}} (a) \ end {pmatrix}} {\ begin {pmatrix} x_ {1} -a_ {1} \ \ x_ {2} -a_ {2} \ end {pmatrix}} \\ & = 0 + {\ begin {pmatrix} 0 & -e \ end {pmatrix}} {\ begynn {pmatrix} x_ {1} - 1 \ \ x_ {2} \ end {pmatrix}} + {\ frac {1} {2}} {\ begin {pmatrix} x_ {1} -1 & x_ {2} \ end {pmatrix}} {\ begin {pmatrix} 0 & -e \\ - e & e \ end {pmatrix}} {\ begin {pmatrix} x_ {1} -1 \\ x_ {2} \ end {pmatrix}} \\ & = - ex_ { 1} x_ {2} + {\ frac {1} {2}} ex_ {2} ^ {2} \ end {align}}}$

litteratur

• Otto Forster : Analyse. Volum 1: Differensial- og integralregning for en variabel. 8. forbedret utgave. Vieweg + Teubner, Wiesbaden 2006, ISBN 3-8348-0088-0 ( Vieweg-studie. Grunnkurs i matematikk ).
• Otto Forster: Analyse. Volum 2: differensialregning i R ⁿ . Vanlige differensialligninger. 7. forbedret utgave. Vieweg + Teubner, Wiesbaden 2006, ISBN 3-8348-0250-6 ( Vieweg-studien. Grunnkurs i matematikk ).
• Bernhard Heck : Beregningsmetoder og evalueringsmodeller for nasjonal kartlegging. Klassiske og moderne metoder. Wichmann, Karlsruhe 1987, ISBN 3-87907-173-X , kapittel 4, 7 og 13 (matematiske modeller og grunnleggende).
• Konrad Königsberger : Analyse. Volum 2. 3., reviderte utgave. Springer, Berlin et al. 2000, ISBN 3-540-66902-7 .

Individuelle bevis

1. ↑ Brook Taylor: Methodus Incrementorum Directa et Inversa. Pearson, London 1717, s. 21 .
2. ^ Königsberger: Analyse. Volum 2. 2000, s. 66.