Binomial koeffisient

Den binomialkoeffisienten er en matematisk funksjon som kan brukes til å løse en av de grunnleggende problemer med kombinatorikk . Den indikerer på hvor mange forskjellige måter man kan velge bestemte objekter fra et sett med forskjellige objekter (uten å erstatte, uten å ta hensyn til rekkefølgen). Binomialkoeffisienten er antall delelementer til et element-sett. ${\ displaystyle k}$${\ displaystyle n}$${\ displaystyle k}$${\ displaystyle n}$

"49 over 6" i Tyskland eller "45 over 6" i Østerrike og Sveits er z. B. antall mulige trekninger i lotteriet (uten å ta hensyn til tilleggstallet).

En binomial koeffisient avhenger av to naturlige tall og . Han vil bli merket med symbolet ${\ displaystyle n}$${\ displaystyle k}$

${\ displaystyle {\ binom {n} {k}}}$

skrevet og snakket som “n over k”, “k out of n” eller “n deep k”. Den engelske forkortelsen nCr for n select r finnes på lommeregner.

Disse tallene ble kalt fordi de fremstår som koeffisienter i binomialens krefter ; den såkalte binomiale teorem gjelder : ${\ displaystyle x + y}$

${\ displaystyle {\ begin {align} (x + y) ^ {n} & = {\ binom {n} {0}} x ^ {n} + {\ binom {n} {1}} x ^ {n -1} y + \ dotsb + {\ binom {n} {n-1}} xy ^ {n-1} + {\ binom {n} {n}} y ^ {n} \\ & = \ sum _ {k = 0} ^ {n} {\ binom {n} {k}} x ^ {nk} y ^ {k} \ end {align}}}$

En utvidelse av binomialkoeffisienten avledet fra kombinatorikk er den generelle binomialkoeffisienten , som brukes i analysen .

definisjon

For et komplekst tall og et ikke-negativt heltall er binomialkoeffisienten "n over k" definert som følger: ${\ displaystyle n}$ ${\ displaystyle k}$

${\ displaystyle {\ begin {align} {\ binom {n} {k}} & = {\ frac {n} {1}} \ cdot {\ frac {n-1} {2}} \ dotsm {\ frac {n- (k-1)} {k}} \\ & = {\ frac {n \ cdot (n-1) \ dotsm (nk + 1)} {k!}} \\ & = \ prod _ { j = 1} ^ {k} {\ frac {n + 1-j} {j}}, \ end {justert}}}$

hvor betegner den faktorielle av . Det tomme produktet ( ) er inkludert . ${\ displaystyle k!}$${\ displaystyle k}$${\ displaystyle k = 0}$${\ displaystyle 1}$

Hvis det er et ikke-negativt heltall med , kan definisjonen kjent fra kombinatorikk brukes: ${\ displaystyle n}$${\ displaystyle n \ geq k}$

${\ displaystyle {\ binom {n} {k}} = {\ frac {n!} {k! \ cdot (nk)!}}}$

eiendommer

Hvis begrensningen også gjøres til ikke-negative heltall, gjelder følgende: ${\ displaystyle k}$${\ displaystyle n}$

• ${\ displaystyle {\ tbinom {n} {k}}}$er alltid et ikke-negativt heltall. Er , så er det , ellers er det .${\ displaystyle k \ leq n}$${\ displaystyle {\ tbinom {n} {k}} \ geq 1}$${\ displaystyle {\ tbinom {n} {k}} = 0}$
• ${\ displaystyle {\ binom {n} {0}} = 1 = {\ binom {n} {n}}}$
• ${\ displaystyle {\ binom {n} {1}} = n = {\ binom {n} {n-1}}}$
• ${\ displaystyle {\ binom {n} {k}} = {\ frac {n-k + 1} {k}} {\ binom {n} {k-1}}}$
• ${\ displaystyle {\ binom {n} {k}} = {\ frac {n} {k}} \ cdot {\ binom {n-1} {k-1}} \ Leftrightarrow k \ cdot {\ binom {n } {k}} = n \ cdot {\ binom {n-1} {k-1}}}$
• ${\ displaystyle {\ binom {n + 1} {k + 1}} = {\ binom {n} {k}} + {\ binom {n} {k + 1}}}$. For er den rette summen .${\ displaystyle n = k}$${\ displaystyle {\ tbinom {n} {n + 1}} = 0}$

I det generelle tilfellet med reelle eller komplekse verdier for , kan noen av uttrykkene gitt her bli udefinerte i den forstand som er gitt ovenfor, hvis de ikke lenger skal være hele og ikke-negative; dette gjelder uttalelsene , og . Det viser seg imidlertid at disse påstandene blir riktig hvis, i samsvar med den analytiske generalisering under, det er beta-funksjon også tillatt for komplekse verdier. ${\ displaystyle n}$${\ displaystyle k}$${\ displaystyle 1 = {\ tbinom {n} {n}}}$${\ displaystyle n = {\ tbinom {n} {n-1}}}$${\ displaystyle {\ tbinom {n} {n + 1}} = 0}$${\ displaystyle k}$

Symmetri av binomiale koeffisienter

Binomiale heltallskoeffisienter er symmetriske i betydningen

${\ displaystyle {\ binom {n} {k}} = {\ binom {n} {nk}}}$

for alle ikke-negative og . ${\ displaystyle n}$${\ displaystyle k}$

bevis

${\ displaystyle {\ begin {align} {\ binom {n} {nk}} & = {\ frac {n!} {(nk)! \ cdot (n- (nk))!}} \\ & = { \ frac {n!} {(nk)! \ cdot k!}} \\ & = {\ frac {n!} {k! \ cdot (nk)!}} \\ & = {\ binom {n} { k}} \ end {align}}}$

eksempel

${\ displaystyle {\ binom {5} {3}} = {\ binom {5} {5-3}} = {\ binom {5} {2}}}$

${\ displaystyle {\ binom {5} {3}} = {\ frac {5!} {3! \ cdot (5-3)!}} = {\ frac {5!} {3! \ cdot 2!} } = {\ frac {1 \ cdot 2 \ cdot 3 \ cdot 4 \ cdot 5} {(1 \ cdot 2 \ cdot 3) \ cdot (1 \ cdot 2)}} = {\ frac {4 \ cdot 5} {1 \ cdot 2}} = 10}$

${\ displaystyle {\ binom {5} {2}} = {\ frac {5!} {2! \ cdot (5-2)!}} = {\ frac {5!} {2! \ cdot 3!} } = {\ frac {1 \ cdot 2 \ cdot 3 \ cdot 4 \ cdot 5} {(1 \ cdot 2) \ cdot (1 \ cdot 2 \ cdot 3)}} = {\ frac {4 \ cdot 5} {1 \ cdot 2}} = 10}$

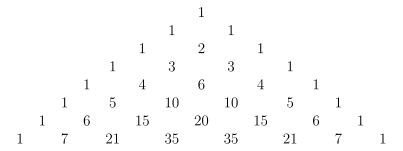
Rekursiv representasjon og Pascals trekant

For hele tall og med kan binomiale koeffisienter også bestemmes ved hjelp av følgende rekursjonsregel : ${\ displaystyle n}$${\ displaystyle k}$${\ displaystyle 0 \ leq k \ leq n}$${\ displaystyle \ textstyle {\ binom {n} {k}}}$

${\ displaystyle {\ binom {n} {0}} = 1 = {\ binom {n} {n}}}$ for alle ${\ displaystyle n \ geq 0}$

${\ displaystyle {\ binom {n + 1} {k + 1}} = {\ binom {n} {k}} + {\ binom {n} {k + 1}}}$for alle og for alle med${\ displaystyle n> 0}$${\ displaystyle k}$${\ displaystyle 0 \ leq k <n}$

Med deres hjelp er det enkelt å bestemme alle binomiale koeffisienter opp til en gitt grense for , en ordning for dette er Pascal-trekanten : Den rekursive delen der tilsvarer det faktum at hvert tall er summen av de to tallene over det. ${\ displaystyle n}$

Bevis:

${\ displaystyle {\ begin {align} {\ binom {n} {k}} + {\ binom {n} {k + 1}} & = {\ frac {n!} {k! \ cdot (nk)! }} + {\ frac {n!} {(k + 1)! \ cdot (n- (k + 1))!}} \\ [. 5em] & = {\ frac {(k + 1) \ cdot n!} {(k + 1) \ cdot k! \ cdot (nk)!}} + {\ frac {n! \ cdot (nk)} {(k + 1)! \ cdot (nk-1)! \ cdot (nk)}} \\ [. 5em] & = {\ frac {(k + 1) \ cdot n!} {(k + 1)! \ cdot (nk)!}} + {\ frac {n! \ cdot (nk)} {(k + 1)! \ cdot (nk)!}} \\ [. 5em] & = {\ frac {(k + 1) \ cdot n! + n! \ cdot (nk) )} {(k + 1)! \ cdot (nk)!}} \\ [. 5em] & = {\ frac {n! \ cdot ((k + 1) + (nk))} {(k + 1 )! \ cdot (nk)!}} \\ [. 5em] & = {\ frac {n! \ cdot (n + 1)} {(k + 1)! \ cdot (nk)!}} \\ [ . 5em] & = {\ frac {(n + 1)!} {(K + 1)! \ Cdot ((n + 1) - (k + 1))!}} \\ [. 5em] & = { \ binomial {n + 1} {k + 1}} \ end {justert}}}$

Koeffisienten finner du i -th-linjen i -th-posisjonen (begge teller fra null!): ${\ displaystyle {\ tbinom {n} {k}}}$${\ displaystyle n}$${\ displaystyle k}$

Den samme trekanten er representert i symbolene: ${\ displaystyle {\ tbinom {n} {k}}}$

Algoritme for effektiv beregning

Det er en effektiv algoritme for heltall , som er produktformelen ${\ displaystyle n}$

${\ displaystyle {n \ select k} = \ prod _ {i = 1} ^ {k} {\ frac {n + 1-i} {i}}}$

av binomialkoeffisienten. På grunn av den konstante endringen mellom multiplikasjon og divisjon, vokser ikke mellomresultatene unødvendig. I tillegg er alle mellomresultater også naturlige tall.

For å unngå unødvendig beregningsinnsats beregnes binomialkoeffisienten i tilfelle : ${\ displaystyle k> n / 2}$

${\ displaystyle {n \ choose nk} = {n \ select k}}$

Følgende pseudokode klargjør beregningen:

binomialkoeffizient(n, k)
1  wenn 2*k > n dann k = n-k
2  ergebnis = 1
3  für i = 1 bis k
4      ergebnis = ergebnis * (n + 1 - i) / i
5  rückgabe ergebnis

Kalkulatorer bruker også denne beregningsmetoden hvis de tilbyr funksjonen. Ellers ville databehandlingskapasiteten være oppbrukt. Merkingen av funksjonstasten med nCr beskriver rekkefølgen på inngangsverdiene i infiksnotasjon ; først antall elementer n, deretter funksjonstasten Kombinasjoner, deretter antall valgte objekter r ( betegnet med k i artikkelen ). ${\ displaystyle n = 69}$

Beregningen nPr ( permutasjoner ) tar hensyn til permutasjonene til r- elementene, divisjon av er utelatt: ${\ displaystyle r!}$

${\ displaystyle P (n, r) = {\ frac {n!} {(nr)!}}}$.

Binomialkoeffisienten i kombinatorikk

I kombinatorisk telling er det

${\ displaystyle {\ binom {n} {k}} = {\ frac {n!} {k! \ cdot (nk)!}}}$

antall kombinasjoner uten repetisjon av elementer av elementer. På grunn av denne egenskapen spiller binomialkoeffisienten en sentral rolle i kombinatorikk og brukes i beregningen og i formlene til andre kombinatoriske størrelser. ${\ displaystyle k}$${\ displaystyle n}$

Illustrasjon med mengder

Sammenlign også: Kombinasjon (kombinatorikk) → Sett representasjon

En annen tolkning av kombinasjoner uten repetisjon av k ut av n-elementer er antall delelementer for alle element av et elementelement . ${\ displaystyle k}$${\ displaystyle n}$

Det kan tolkes som følger:

versjon 1

Først teller man alt - tupler med parvis forskjellige elementer som kan settes sammen fra -elementets innledende sett. Det er alternativer for å velge det første tupelelementet. Etter et valg av dette først er det bare alternativer for det andre elementet, etter at det bare er valgt for det tredje osv., Opp til alternativene for det tredje og siste tupelelementet. Antallet alle tuplene satt sammen på denne måten er derfor et produkt av faktorer som ved hjelp av fakultetet også kan noteres som . Nå er imidlertid nøyaktig hver av de tellede -Tuplene permutasjoner av hverandre og tilsvarer derfor en og samme -Element-undergruppe. Etter å ha delt på denne “tellende multiplikasjonen”, blir resultatet faktisk antall undersett. ${\ displaystyle k}$${\ displaystyle n}$${\ displaystyle n}$${\ displaystyle n-1}$${\ displaystyle n-2}$${\ displaystyle n-k + 1}$${\ displaystyle k}$${\ displaystyle k}$${\ displaystyle n \ cdot (n-1) \ cdot (n-2) \ dotsm (n-k + 2) \ cdot (n-k + 1)}$${\ displaystyle k}$${\ displaystyle {\ tfrac {n!} {(nk)!}}}$${\ displaystyle k!}$${\ displaystyle k}$${\ displaystyle k}$${\ displaystyle {\ tfrac {n!} {k! \ cdot (nk)!}} = {\ tbinom {n} {k}}}$

Variant 2

En annen, mer symmetrisk illustrasjon understreker ikke handlingen med å velge fra elementer, men snarere aspektet ved å bryte det ned i to undergrupper av og elementer. Anta at en -element utgangs tuple består av røde og hvite elementer som på en eller annen måte er stilt opp. Hvis man danner alle permutasjoner av denne sekvensen, kan de ikke skilles fra hverandre når det gjelder farge, fordi permutasjoner av de røde elementene med hverandre ikke endrer noe i fargesekvensen, like lite som noen gang uavhengige permutasjoner i de hvite. Så det er bare fargekodede sekvenser av lengden med alle mulige forskjellige oppgaver, hver med røde elementer. Imidlertid kan hver sekvens nå tildeles unikt til et av delelementene til et element. Det samme gjelder på grunn av symmetrien til rødt og hvitt eller av og også for de komplementære delelementene. Totalt antall av disse delmengdene er dermed hver . ${\ displaystyle k}$${\ displaystyle n}$${\ displaystyle k}$${\ displaystyle l: = nk}$${\ displaystyle n = l + k}$${\ displaystyle k}$${\ displaystyle l}$${\ displaystyle (k + l)!}$${\ displaystyle k! \ cdot l!}$${\ displaystyle k!}$${\ displaystyle l!}$${\ displaystyle {\ tfrac {(k + l)!} {k! \ cdot l!}} = {\ tbinom {k + l} {k}} = {\ tbinom {k + l} {l}}}$${\ displaystyle k + l}$${\ displaystyle k}$${\ displaystyle k}$${\ displaystyle k + l}$${\ displaystyle k}$${\ displaystyle l}$ ${\ displaystyle l}$${\ displaystyle {\ tbinom {k + l} {k}} = {\ tbinom {n} {k}} = {\ tbinom {n} {nk}} = {\ tbinom {k + l} {l}} }$

eksempel

Følgende gjelder antall mulige loddtrekninger eller billetter til den tyske Lotto 6 av 49 (uten tilleggsnummer eller supernummer):

${\ displaystyle {\ tbinom {49} {6}} = 13,983,816 \ ca 14 \ {\ text {million}}}$

Åpenbart er det nøyaktig en måte å velge 6 riktige tall på. teller mulighetene for 0 riktige, nemlig å velge alle 6 tipsene fra de 43 feilene. Antall forskjellige tips med 5 riktige tall er veldig enkelt , fordi det er 6 måter å velge bare 5 av de 6 tallene som er tegnet (eller å utelate et av dem), og i hvert tilfelle er det måter å plassere det utelatte tipset på ett av de 43 feil tallene. Generelt sett er antall forskjellige tips med riktige på 6 resultater fra 49 med samme hensyn . Ved 6, 0 og 5 høyre merker man knapt at faktorene som brukes , og faktisk enkle binomiale koeffisienter. Summen av alle tipsetallene som er nevnt, resulterer i det totale antallet 13983816 av alle mulige tips - dette følger av Vandermonde-identiteten gitt nedenfor . ${\ displaystyle {\ tbinom {43} {6}}}$${\ displaystyle 6 \ cdot 43 = 258}$${\ displaystyle 43 = 49-6}$${\ displaystyle r}$${\ displaystyle {\ tbinom {6} {r}} \ cdot {\ tbinom {43} {6-r}}}$${\ displaystyle 1 = {\ tbinom {6} {6}} = {\ tbinom {6} {0}} = {\ tbinom {43} {0}}}$${\ displaystyle 6 = {\ tbinom {6} {5}}}$${\ displaystyle 43 = {\ tbinom {43} {1}}}$

Så sannsynligheten for 6 riktige tall med ett tips er at for 5 riktige tall . For 0 riktige tall er resultatet rundt 44%. Den generelle sannsynligheten for å være riktig er et spesielt tilfelle av den hypergeometriske fordelingen , som kombinerer tre binomiale koeffisienter på denne måten. ${\ displaystyle 1/13983816}$${\ displaystyle 258/13983816}$${\ displaystyle 6096454/13983816}$${\ displaystyle {\ tbinom {6} {r}} \ cdot {\ tbinom {43} {6-r}} / {\ tbinom {49} {6}}}$${\ displaystyle r}$

For flere eksempler, se: Kombinasjon (kombinatorikk) → Eksempler

Kombinatorisk bevis

Den kombinatoriske tolkningen tillater også enkle bevis på forholdet mellom binomiale koeffisienter, for eksempel ved dobbel telling . Eksempel: Følgende gjelder for: ${\ displaystyle 1 \ leq k \ leq n}$

${\ displaystyle {n \ velger k} = {n-1 \ velger k-1} + {n-1 \ velger k}}$

Bevis: La det være et -elementært sett og et fast element. Deretter deles elementets del av to klasser: ${\ displaystyle X}$${\ displaystyle n}$${\ displaystyle x \ i X}$${\ displaystyle k}$${\ displaystyle X}$

• delmengdene som inneholder; de består av, sammen med en delelement av elementet ,${\ displaystyle x}$${\ displaystyle x}$${\ displaystyle (k-1)}$${\ displaystyle (n-1)}$${\ displaystyle X \ setminus \ {x \}}$
• delsettene som ikke inneholder; de er -elementundersett av -elementsettet .${\ displaystyle x}$${\ displaystyle k}$${\ displaystyle (n-1)}$${\ displaystyle X \ setminus \ {x \}}$

Kombinasjonsmengder

Settet med underdeler av alle element i et sett er noen ganger også betegnet på grunn av dets kraft . Så for hvert endelige sett : ${\ displaystyle k}$${\ displaystyle M}$${\ displaystyle {\ tbinom {\ left | M \ right |} {k}}}$${\ displaystyle {\ tbinom {M} {k}}}$${\ displaystyle M}$

${\ displaystyle \ left | {M \ select k} \ right | = {\ left | M \ right | \ velg k}}$

Uttrykk med binomiale koeffisienter

Summer med binomiale koeffisienter

${\ displaystyle \ sum _ {k = 0} ^ {n} {\ binom {n} {k}} = {\ binom {n} {0}} + {\ binom {n} {1}} + \ dotsb + {\ binom {n} {n}} = 2 ^ {n}}$

Denne formelen er basert på et kombinatorisk faktum. Siden det totale antallet delelementer av elementet er -elementbeløpet, blir tallet gitt ved summering av alle delmengdene, altså . Formelen kan også avledes fra binomialsetningen ved å sette. ${\ displaystyle {\ tbinom {n} {k}}}$${\ displaystyle k}$${\ displaystyle n}$${\ displaystyle 2 ^ {n}}$${\ displaystyle x = y = 1}$

Sum med alternerende binomiale koeffisienter

${\ displaystyle \ sum _ {k = 0} ^ {n} (- 1) ^ {k} {\ binom {n} {k}} = {\ binom {n} {0}} - {\ binom {n } {1}} + {\ binom {n} {2}} \ mp \ dotsb + (- 1) ^ {n} {\ binom {n} {n}} = 0}$for .${\ displaystyle n> 0}$

For merkelig følger denne formelen fra symmetrien til binomialkoeffisienten. For alle kan den avledes fra binomialsetningen ved å sette og (eller og ). ${\ displaystyle n}$${\ displaystyle n}$${\ displaystyle x = 1}$${\ displaystyle y = -1}$${\ displaystyle x = -1}$${\ displaystyle y = 1}$

Summer av binomiale koeffisienter med like eller ulige antall valgte objekter

Ved subtraksjon eller tillegg til ovenstående ligninger og etterfulgt av halvering for get: ${\ displaystyle \ textstyle \ sum _ {k = 0} ^ {n} {\ binom {n} {k}} = 2 ^ {n}}$${\ displaystyle \ textstyle \ sum _ {k = 0} ^ {n} (- 1) ^ {k} {\ binom {n} {k}} = 0}$${\ displaystyle n> 0}$

${\ displaystyle \ sum _ {k = 0} ^ {[{\ frac {n} {2}}]} {\ binom {n} {2k}} = 2 ^ {n-1}}$som også ; ${\ displaystyle \ sum _ {k = 0} ^ {[{\ frac {n-1} {2}}]} {\ binom {n} {2k + 1}} = 2 ^ {n-1}}$

hvor [] er gaussiske parenteser .

Summen av forskyvede binomiale koeffisienter

Fra induksjonsstart for alt som bruker rekursjonsregelen for binomiale koeffisienter, er det enkelt å bevise med induksjon ved å bruke rekursjonsregelen igjen: ${\ displaystyle \ textstyle \ sum _ {k = 0} ^ {m = 1} {\ binom {n + k} {n}} = {\ binom {n} {n}} + {\ binom {n + 1 } {n}} = {\ binom {n + 1} {n + 1}} + {\ binom {n + 1} {n}} = {\ binom {n + 1 + 1} {n + 1}} }$${\ displaystyle n}$${\ displaystyle m}$

${\ displaystyle \ sum _ {k = 0} ^ {m} {\ binom {n + k} {n}} = {\ binom {n} {n}} + {\ binom {n + 1} {n} } + \ dotsb + {\ binom {n + m} {n}} = {\ binom {n + m + 1} {n + 1}}}$;

på grunn av symmetrien i sommerene så vel som summen, gjelder også følgende:

${\ displaystyle \ sum _ {k = 0} ^ {m} {\ binom {n + k} {k}} = {\ binom {n} {0}} + {\ binom {n + 1} {1} } + \ dotsb + {\ binom {n + m} {m}} = {\ binom {n + m + 1} {m}} = {\ binom {n + m + 1} {n + 1}}}$.

Vandermonde identitet

${\ displaystyle \ sum _ {j = 0} ^ {k} {\ binom {m} {j}} {\ binom {n} {kj}} = {\ binom {m + n} {k}}.}$

Det er også et kombinasjonsargument her: Høyre side tilsvarer antall delelementer til et element-sett med kuler. Man kan nå forestille seg at kulene har to forskjellige farger: kuler er røde og kuler grønne. Et elementært delmengde består da av et visst antall røde baller og mange grønne baller . For hver mulig indikerer den tilsvarende summen til venstre antall muligheter for en slik inndeling i røde og grønne sfærer. Summen gir totalt antall. Et bevis som ofte oppleves som enkelt, bruker binomialsetningen i formen ${\ displaystyle k}$${\ displaystyle (m + n)}$${\ displaystyle m}$${\ displaystyle n}$${\ displaystyle k}$${\ displaystyle j}$${\ displaystyle kj}$${\ displaystyle j}$

${\ displaystyle (1 + x) ^ {n} = \ sum _ {k = 0} ^ {n} {\ binom {n} {k}} x ^ {k},}$

så vel som tilnærmingen

${\ displaystyle (1 + x) ^ {m} (1 + x) ^ {n} = (1 + x) ^ {m + n}}$

og koeffisient sammenligning.

I et spesielt tilfelle resulterer Vandermondes identitet i følgende formel for kvadratsummen: ${\ displaystyle k = m = n}$

${\ displaystyle \ sum _ {j = 0} ^ {n} {\ binom {n} {j}} ^ {2} = {\ binom {2n} {n}}}$

Divisjonsrester

Er et primtall, og er det da ${\ displaystyle p}$${\ displaystyle n_ {0}, k_ {0} \ in \ {0, \ dotsc, p-1 \}}$${\ displaystyle n_ {1}, k_ {1} \ in \ mathbb {N}}$

${\ displaystyle {\ binom {n_ {0} + pn_ {1}} {k_ {0} + pk_ {1}}} \ equiv {\ binom {n_ {0}} {k_ {0}}} {\ binom {n_ {1}} {k_ {1}}} {\ pmod {p}}.}$

Det betyr at modulo kan beregnes effektivt ved hjelp av representasjonene fra og til basen , nemlig "siffer for siffer". ${\ displaystyle p}$${\ displaystyle {\ tbinom {n} {k}}}$${\ displaystyle n}$${\ displaystyle k}$${\ displaystyle p}$

Binomiale koeffisienter i analyse

generalisering

En generalisering som spiller en rolle i kalkulus oppnås hvis man tillater et vilkårlig komplekst tall , men fortsetter å anta at det er et helt tall. I dette tilfellet er det ${\ displaystyle n}$ ${\ displaystyle \ alpha}$${\ displaystyle k}$

${\ displaystyle {\ binom {\ alpha} {k}} = {\ begin {cases} {\ frac {\ alpha (\ alpha -1) (\ alpha -2) \ dotsm (\ alpha - (k-1) )} {k!}}, & {\ text {if}} \ quad k> 0 \\ 1, & {\ text {if}} \ quad k = 0 \\ 0, & {\ text {if}} \ quad k <0 \ end {cases}}}$

binomialkoeffisienten " over " (det tomme produktet i saken er definert som 1). Denne definisjonen stemmer overens med ikke-negativt heltall med den kombinatoriske definisjonen (dvs. definisjonen av som antall delelementer for alle element i et fast elementært sett), og for ikke-negativ med den algebraiske definisjonen (dvs. definisjonen av som produktet ). ${\ displaystyle \ alpha}$${\ displaystyle k}$${\ displaystyle k = 0}$${\ displaystyle \ alpha}$${\ displaystyle {\ tbinom {\ alpha} {k}}}$${\ displaystyle k}$${\ displaystyle \ alpha}$${\ displaystyle k}$${\ displaystyle {\ tbinom {\ alpha} {k}}}$${\ displaystyle {\ tfrac {\ alpha} {1}} \ cdot {\ tfrac {\ alpha -1} {2}} \ dotsm {\ tfrac {\ alpha - (k-1)} {k}}}$

For eksempel er

${\ displaystyle {2 {,} 5 \ select 2} = {\ frac {2 {,} 5 \ cdot 1 {,} 5} {2!}} = {\ frac {3 {,} 75} {2} } = 1 {,} 875}$

og

${\ displaystyle {-1 \ velg k} = {\ frac {(-1) (- 2) \ dotsm (-k)} {k!}} = (- 1) ^ {k}.}$

Den andre parameteren kan også generaliseres til en hvilken som helst kompleks oppgave hvis beta-funksjonen brukes til å definere: ${\ displaystyle k}$${\ displaystyle z}$ ${\ displaystyle \ mathrm {B} (x, y)}$${\ displaystyle \ alpha \ in \ mathbb {C} \ setminus \ {- 1, -2, -3, \ dotsc \}}$

${\ displaystyle {\ binom {\ alpha} {z}} = {\ frac {1} {(\ alpha +1) \, \ mathrm {B} (z + 1, \ alpha -z + 1)}} = {\ frac {\ Gamma (\ alpha +1)} {\ Gamma (z + 1) \, \ Gamma (\ alpha -z + 1)}},}$

hvor betegner de gammafunksjonen . Hvis det er eller et negativt heltall, er verdien på høyre side 0 fordi de ikke-positive heltallene er (eneste) poler av . ${\ displaystyle \ Gamma (z)}$${\ displaystyle z}$${\ displaystyle \ alpha -z}$${\ displaystyle \ Gamma (z)}$

Åpenbart gjelder symmetriforholdet fremdeles

${\ displaystyle {\ binom {\ alpha} {z}} = {\ binom {\ alpha} {\ alpha -z}}}$,

spesielt

${\ displaystyle {\ binom {\ alpha} {1}} = {\ binom {\ alpha} {\ alpha -1}} = \ alpha}$,

${\ displaystyle {\ binom {\ alpha} {0}} = {\ binom {\ alpha} {\ alpha}} = 1}$

og med en ikke-negativ helhet ${\ displaystyle m}$

${\ displaystyle {\ binom {\ alpha} {- m}} = {\ binom {\ alpha} {\ alpha + m}} = 0}$.

For å trekke ut tegnet fra den første parameteren, forutsatt at det er et heltall, forholdet

${\ displaystyle {\ binom {- \ alpha} {k}} = (- 1) ^ {k} {\ binom {\ alpha + k-1} {k}}}$

spesifisere.

Generelt for kompleks , forholdet ${\ displaystyle \ alpha}$${\ displaystyle z}$

${\ displaystyle {\ binom {- \ alpha} {z}} = \ left (\ cos (\ pi z) + \ sin (\ pi z) \ cot (\ pi \ alpha) \ right) {\ binom {\ alpha + z-1} {z}}}$.

De multinomiale koeffisientene , som er nødvendige når generaliseringen av binomialet til multinomialteoremet , gir en ytterligere generalisering .

Binomial-serien

For og med deg opprettholde forholdet ${\ displaystyle n \ in \ mathbb {N} _ {0}}$${\ displaystyle z \ in \ mathbb {C} \ setminus \ {1 \}}$${\ displaystyle | z | \ geq 1}$

${\ displaystyle \ sum _ {k = 0} ^ {\ infty} {\ binom {k} {n}} {\ frac {1} {z ^ {k + 1}}} = \ sum _ {k = n } ^ {\ infty} {\ binom {k} {n}} {\ frac {1} {z ^ {k + 1}}} = {\ frac {1} {(z-1) ^ {n + 1 }}},}$

som er en generalisering av den geometriske serien og tilhører binomial-serien .

Hvis , i tillegg til , følgende serie konvergerer i henhold til ${\ displaystyle | z | \ leq 1}$${\ displaystyle z \ neq -1}$${\ displaystyle \ alpha \ in \ mathbb {C}}$

${\ displaystyle \ sum _ {k = 0} ^ {\ infty} {\ binom {\ alpha} {k}} z ^ {k} = (1 + z) ^ {\ alpha}.}$

Mer eksakte forhold for og er gitt i artikkelen Binomial Series . ${\ displaystyle z}$${\ displaystyle \ alpha}$

Sumuttrykk for beta-funksjonen

Et annet forhold kan bevises for alle relativt enkelt med fullstendig induksjon, ${\ displaystyle m, n \ geq 0}$

${\ displaystyle \ sum \ limits _ {k = 0} ^ {n} {\ binom {n} {k}} {\ frac {(-1) ^ {k}} {m + k + 1}} = { \ dfrac {1} {(m + n + 1) \ displaystyle {\ binom {m + n} {m}}}},}$

hvorfra symmetrien umiddelbart

${\ displaystyle \ sum \ limits _ {k = 0} ^ {n} {\ binom {n} {k}} {\ frac {(-1) ^ {k}} {m + k + 1}} = \ sum \ limits _ {k = 0} ^ {m} {\ binom {m} {k}} {\ frac {(-1) ^ {k}} {n + k + 1}}}$

følger. En generalisering for med og leser ${\ displaystyle z, s \ in \ mathbb {C}}$${\ displaystyle -z, -s \ notin \ mathbb {N}}$${\ displaystyle s + z \ neq -1}$

${\ displaystyle \ sum \ limits _ {k = 0} ^ {\ infty} {\ binom {s} {k}} {\ frac {(-1) ^ {k}} {z + k + 1}} = {\ dfrac {1} {(z + s + 1) \ displaystyle {\ binom {z + s} {s}}}} = \ mathrm {B} (z + 1, s + 1).}$

Gaussisk produktrepresentasjon for gammafunksjonen

Den siste formelen fra forrige avsnitt er for ${\ displaystyle -z \ notin \ {0,1,2, \ dotsc, n \}}$

${\ displaystyle \ sum \ limits _ {k = 0} ^ {n} {\ binom {n} {k}} {\ frac {(-1) ^ {k}} {z + k}} = {\ frac {n!} {z \, (z + 1) \, (z + 2) \ dotsm (z + n)}}.}$

Ser du på saken , erstatt brøkene i summen med integraler i henhold til ${\ displaystyle \ operatorname {Re} z> 0}$

${\ displaystyle {\ frac {1} {z + k}} = \ int \ grenser _ {0} ^ {1} t ^ {z + k-1} \ mathrm {d} t}$

og oppsummerer summen av maktene i henhold til de binomiale formlene man oppnår

${\ displaystyle \ sum \ limits _ {k = 0} ^ {n} {\ binom {n} {k}} {\ frac {(-1) ^ {k}} {z + k}} = \ int \ begrenser _ {0} ^ {1} t ^ {z-1} (1-t) ^ {n} \ mathrm {d} t = n ^ {- z} \ int \ limits _ {0} ^ {n} t ^ {z-1} \ left (1 - {\ frac {t} {n}} \ right) ^ {n} \ mathrm {d} t,}$

hvor erstatningen ble brukt for den siste integralen . Tross alt har du ligningen ${\ displaystyle t \ to t / n}$

${\ displaystyle \ int \ limits _ {0} ^ {n} t ^ {z-1} \ left (1 - {\ frac {t} {n}} \ right) ^ {n} \ mathrm {d} t = {\ frac {n ^ {z} \, n!} {z \, (z + 1) \, (z + 2) \ dotsm (z + n)}},}$

hvorfra den gaussiske produktrepresentasjonen av gammafunksjonen kommer direkte fra grenseovergangen , ${\ displaystyle n \ to \ infty}$

${\ displaystyle \ Gamma (z) = \ lim \ limits _ {n \ to \ infty} {\ frac {n ^ {z} \, n!} {z \, (z + 1) \, (z + 2 ) \ dotsm (z + n)}},}$

resultater.

Digamma-funksjon og Euler-Mascheroni konstant

For med gjelder ${\ displaystyle m, n \ in \ mathbb {N}}$${\ displaystyle m \ leq n}$

${\ displaystyle \ sum \ limits _ {k = 1} ^ {m} {\ binom {n} {mk}} {\ frac {(-1) ^ {k-1}} {k}} = {\ binom {n} {m}} \ sum \ limits _ {k = nm + 1} ^ {n} {\ frac {1} {k}},}$

som også kan bevises ved induksjon . For det spesielle tilfellet er denne ligningen forenklet til ${\ displaystyle m}$${\ displaystyle n = m}$

${\ displaystyle \ sum \ limits _ {k = 1} ^ {n} {\ binom {n} {k}} {\ frac {(-1) ^ {k-1}} {k}} = \ sum \ begrenser _ {k = 1} ^ {\ infty} {\ binom {n} {k}} {\ frac {(-1) ^ {k-1}} {k}} = \ sum \ limits _ {k = 1} ^ {n} {\ frac {1} {k}} = H_ {n},}$

hvor er sekvensen til de harmoniske tallene, dvs. delsummen til den harmoniske serien . Konvertering av venstresummen til en serie (grense i stedet for ) er tillatt på grunn av for${\ displaystyle H_ {n}}$${\ displaystyle \ infty}$${\ displaystyle n}$${\ displaystyle {\ tbinom {n} {k}} = 0}$${\ displaystyle n <k.}$

${\ displaystyle H_ {n}}$ er derimot representabel som

${\ displaystyle H_ {n} = \ psi (n + 1) - \ psi (1) = \ psi (n + 1) + \ gamma}$

med digamma-funksjonen og Euler-Mascheroni-konstanten${\ displaystyle \ psi (n)}$ ${\ displaystyle \ gamma.}$

${\ displaystyle \ psi (n)}$kan fortsettes til komplekse verdier - bortsett fra negative heltall. Så du får raden ${\ displaystyle z}$

${\ displaystyle \ sum \ limits _ {k = 1} ^ {\ infty} {\ binom {z} {k}} {\ frac {(-1) ^ {k-1}} {k}} = \ psi (z + 1) + \ gamma}$

som en kompleks interpolering av sekvensen av harmoniske tall.

Trivia

Den bokstavelige oversettelsen av " over " til engelsk " over " betegner ikke binomialkoeffisienten , men brøkdelen . " Velg " er riktig . ${\ displaystyle n}$${\ displaystyle k}$${\ displaystyle n}$${\ displaystyle k}$${\ displaystyle {\ tbinom {n} {k}}}$${\ displaystyle {\ tfrac {n} {k}}}$${\ displaystyle n}$${\ displaystyle k}$

weblenker

• Last ned fra BigAl. (Lite, gratis og plattformuavhengig program, blant annet for nøyaktig beregning av binomialkoeffisienten; med kildekode).
• Online beregning av binomiale koeffisienter.

Individuelle bevis

1. ↑ Disquisitiones gener circa seriem infinitam 1 + ... . 1813, s. 26 (også i Carl Friedrich Gauß: Werke. Bind 3, s. 145 ).