Bueskinn og bueskinn

Den arcsinus - skriftlig eller  - og den arccosinus (eller også arccosinus ) - skriftlig eller  - er inverse funksjoner av den (hensiktsmessig) begrenses sinus- eller cosinus-funksjon . Sinus og cosinus er funksjoner som kartlegger en vinkel til en verdi i intervallet ; som deres omvendte funksjoner kartlegger buesine og buesine en verdi fra igjen til en tilhørende vinkel. Siden sinus og cosinus er periodiske funksjoner, er det et uendelig antall tilknyttede vinkler for hver verdi fra . Derfor, for å invertere sinus og cosinus, er deres definisjonssett begrenset til intervallet for sinus og til for cosinus. Sinus og cosinus er strengt ensformige i disse intervallene og er derfor reversible. ${\ displaystyle \ arcsin}$${\ displaystyle \ operatorname {asin}}$${\ displaystyle \ arccos}$${\ displaystyle \ operatorname {acos}}$ ${\ displaystyle [-1.1]}$${\ displaystyle [-1.1]}$${\ displaystyle [-1.1]}$${\ displaystyle [- {\ tfrac {\ pi} {2}}, {\ tfrac {\ pi} {2}}]}$${\ displaystyle [0, \ pi]}$

Sammen med arktangenten som den omvendte funksjonen til den (også passende begrensede) tangenten , utgjør arktangenten og arkkosinen kjernen i klassen av arktopiske funksjoner . På grunn av den vanlige stavemåten nylig for inverse funksjoner, stikker navnet spredt til kalkulatorene stavemåter og den klassiske stavemåten eller fortrenger det som kan forveksles med gjensidighetene til sinus og cosinus ( cosecant og secant kan resultere).${\ displaystyle f ^ {- 1}}$${\ displaystyle \ sin ^ {- 1}}$${\ displaystyle \ cos ^ {- 1}}$${\ displaystyle \ arcsin}$${\ displaystyle \ arccos}$

Definisjoner

Sinusfunksjonen er -periodisk og ikke injiserende innen en periode . Derfor må domenet deres begrenses på en passende måte for å oppnå en reversibel unik funksjon. Siden det er flere muligheter for denne begrensningen, snakker vi om buegrener. Vanligvis hovedgrenen (eller hovedverdien) ${\ displaystyle 2 \ pi}$

${\ displaystyle \ arcsin \ colon [-1,1] \ to \ left [- {\ frac {\ pi} {2}}, {\ frac {\ pi} {2}} \ right],}$

den inverse funksjonen til begrensningen av sinusfunksjonen til intervallet blir vurdert. ${\ displaystyle \ sin | _ {\ left [- {\ frac {\ pi} {2}}, {\ frac {\ pi} {2}} \ right]}}$${\ displaystyle \ left [- {\ frac {\ pi} {2}}, {\ frac {\ pi} {2}} \ right],}$

Analogt med arkkosinen, er hovedgrenen til arkkosinen definert som den omvendte funksjonen til . Dette resulterer i med ${\ displaystyle \ cos | _ {[0, \ pi]}}$

${\ displaystyle \ arccos \ colon [-1,1] \ til [0, \ pi]}$

også en bijektiv funksjon. Midler

${\ displaystyle \ arccos (x) + \ arcsin (x) = {\ frac {\ pi} {2}}}$

disse to funksjonene kan konverteres til hverandre.

eiendommer

	Arcsine	Arccosine
Funksjonsgraf
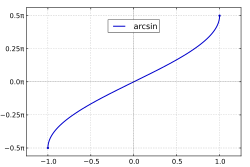
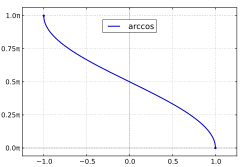
Definisjonssett	${\ displaystyle [-1.1]}$	${\ displaystyle [-1.1]}$
Bildesett	${\ displaystyle \ left [- {\ frac {\ pi} {2}}, {\ frac {\ pi} {2}} \ right]}$	${\ displaystyle [0, \ pi]}$
monotoni	strengt monotont økende	strengt avtagende monotont
Symmetrier	Odd-funksjon ( punkt symmetri til ):${\ displaystyle (0,0)}$ ${\ displaystyle \ arcsin (-x) = - \ arcsin (x)}$	Punkt symmetri også ${\ displaystyle \ left (0, {\ tfrac {\ pi} {2}} \ right) \ colon}$ ${\ displaystyle \ arccos (x) = \ pi - \ arccos (-x)}$
Asymptoter	Nei	Nei
nullpunkt	${\ displaystyle 0}$	${\ displaystyle 1}$
Hopp poeng	Nei	Nei
Poler	Nei	Nei
Ekstremer	Globalt maksimum på plass , globalt minimum på plass${\ displaystyle {\ tfrac {\ pi} {2}}}$${\ displaystyle 1}$ ${\ displaystyle - {\ tfrac {\ pi} {2}}}$${\ displaystyle -1}$	Globalt maksimum på plass , globalt minimum på plass${\ displaystyle \ pi}$${\ displaystyle -1}$ ${\ displaystyle 0}$${\ displaystyle 1}$
Vendepunkter	${\ displaystyle (0,0)}$	${\ displaystyle \ left (0, {\ frac {\ pi} {2}} \ right)}$

Formler for negative argumenter

På grunn av symmetriegenskapene gjelder følgende:

${\ displaystyle \ arcsin (-x) = - \ arcsin (x)}$

${\ displaystyle \ arccos (-x) = \ pi - \ arccos (x)}$

Serien utvikler seg

Den Taylor-serien arcsinus oppnås ved å utvikle derivatet inn i en binominalrekken og deretter integrere det, det er gitt ved:

${\ displaystyle {\ begin {align} \ arcsin (x) & = \ sum _ {k = 0} ^ {\ infty} {\ frac {(2k-1) !!} {(2k) !!}} { \ frac {x ^ {2k + 1}} {2k + 1}} = \ sum _ {k = 0} ^ {\ infty} {\ binom {2k} {k}} {\ frac {x ^ {2k + 1}} {4 ^ {k} (2k + 1)}} \\ & = {x + {\ frac {1} {2}} \ cdot {\ frac {x ^ {3}} {3}} + {\ frac {1 \ cdot 3} {2 \ cdot 4}} \ cdot {\ frac {x ^ {5}} {5}} + {\ frac {1 \ cdot 3 \ cdot 5} {2 \ cdot 4 \ cdot 6}} \ cdot {\ frac {x ^ {7}} {7}} + \ dotsb} \ end {justert}}}$

Begrepet betegner det dobbelte fakultetet . ${\ displaystyle k !!}$

De Taylor serie arccosinus resultatene fra forholdet : ${\ displaystyle \ arccos x = {\ tfrac {\ pi} {2}} - \ arcsin x}$

${\ displaystyle \ arccos (x) = {\ frac {\ pi} {2}} - \ sum _ {k = 0} ^ {\ infty} {\ frac {(2k-1) !!} {(2k) !!}} {\ frac {x ^ {2k + 1}} {2k + 1}} = {\ frac {\ pi} {2}} - \ sum _ {k = 0} ^ {\ infty} {\ binomial {2k} {k}} {\ frac {x ^ {2k + 1}} {4 ^ {k} (2k + 1)}}}$

Begge seriene har konvergensradius 1.

Integrerte representasjoner

De integrerte representasjonene av buesagen og buesinen er gitt av:

${\ displaystyle \ arcsin (x) = \ int \ limits _ {0} ^ {x} {\ frac {\ mathrm {d} t} {\ sqrt {1-t ^ {2}}}}}$

${\ displaystyle \ arccos (x) = \ int \ limits _ {x} ^ {1} {\ frac {\ mathrm {d} t} {\ sqrt {1-t ^ {2}}}}}$

Sammenkoblinger med sinus og cosinus

Følgende formler gjelder for buefunksjonene:

${\ displaystyle \ sin (\ arccos (x)) = {\ sqrt {1-x ^ {2}}}}$, fordi gjelder for og .${\ displaystyle y = \ arccos (x)}$${\ displaystyle y \ in \ left [0, {\ pi} \ right]}$${\ displaystyle \ sin (y) = {\ sqrt {1- \ cos ^ {2} (y)}}$

${\ displaystyle \ cos (\ arcsin (x)) = {\ sqrt {1-x ^ {2}}}}$, fordi gjelder for og .${\ displaystyle y = \ arcsin (x)}$${\ displaystyle y \ in \ left [- {\ frac {\ pi} {2}}, {\ frac {\ pi} {2}} \ right]}$${\ displaystyle \ cos (y) = {\ sqrt {1- \ sin ^ {2} (y)}}$

${\ displaystyle \ sin (\ arctan (x)) = {\ frac {x} {\ sqrt {1 + x ^ {2}}}}}$, fordi gjelder for og .${\ displaystyle y = \ arctan (x)}$${\ displaystyle y \ in \ left] - {\ frac {\ pi} {2}}, {\ frac {\ pi} {2}} \ right [}$${\ displaystyle \ sin (y) = {\ frac {\ tan (y)} {\ sqrt {1+ \ tan ^ {2} (y)}}}$

${\ displaystyle \ cos (\ arctan (x)) = {\ frac {1} {\ sqrt {1 + x ^ {2}}}}}$, fordi gjelder for og .${\ displaystyle y = \ arctan (x)}$${\ displaystyle y \ in \ left] - {\ frac {\ pi} {2}}, {\ frac {\ pi} {2}} \ right [}$${\ displaystyle \ cos (y) = {\ frac {1} {\ sqrt {1+ \ tan ^ {2} (y)}}}}$

Forholdet til arktangenten

Av spesiell betydning i eldre programmeringsspråk uten implementerte bueformede og bueformede funksjoner er følgende forhold, som gjør det mulig å beregne bueformet og bueformet fra arktangenten som kan ha blitt implementert. Basert på formlene ovenfor gjelder følgende

${\ displaystyle \ arcsin (x) = \ arctan \ left ({\ frac {x} {\ sqrt {1-x ^ {2}}} \ right)}$

${\ displaystyle \ arccos (x) = {\ frac {\ pi} {2}} - \ arctan \ left ({\ frac {x} {\ sqrt {1-x ^ {2}}}} \ right)}$

for Definert på denne måten blir disse to ligningene også korrekte. Alternativt kan du også ${\ displaystyle | x | <1.}$${\ displaystyle \ arctan \ left ({\ tfrac {1} {0}} \ right): = \ lim _ {t \ to \ infty} \ arctan (t) = {\ tfrac {\ pi} {2}} ,}$${\ displaystyle x = \ pm 1}$

${\ displaystyle \ arcsin (x) = 2 \ arctan \ left ({\ frac {x} {1 + {\ sqrt {1-x ^ {2}}}}} \ right)}$

${\ displaystyle \ arccos (x) = {\ frac {\ pi} {2}} - 2 \ arctan \ left ({\ frac {x} {1 + {\ sqrt {1-x ^ {2}}}} } \ Ikke sant)}$

bruke det som følger av ovennevnte ved å bruke den funksjonelle ligningen til arktangenten og gjelder for. Den sistnevnte kan også brukes for ${\ displaystyle | x | \ leq 1}$${\ displaystyle -1 <x \ leq 1}$

${\ displaystyle \ arccos (x) = 2 \ arctan \ left ({\ sqrt {\ frac {1-x} {1 + x}}} høyre)}$

forenkle.

Tilleggssetninger

→ Hovedartikkel: Tilleggssetninger for buefunksjoner (trigonometri)

Tilsetningssetningene for buesvin og arkkosin kan fås ved hjelp av tilleggssetningene for sinus og cosinus :

${\ displaystyle \ arcsin x + \ arcsin y = \ left \ {{\ begin {matrix} \ arcsin (\ sin (\ arcsin x + \ arcsin y)) = \ arcsin \ left (x {\ sqrt {1-y ^ {2}}} + y {\ sqrt {1-x ^ {2}}} \ right) & {\ text {if}} xy \ leq 0 {\ text {or}} x ^ {2} + y ^ {2} \ leq 1 \\\ pi - \ arcsin (\ sin (\ arcsin x + \ arcsin y)) = \ pi - \ arcsin \ left (x {\ sqrt {1-y ^ {2}}} + y {\ sqrt {1-x ^ {2}}} \ right) & {\ text {if}} x> 0 {\ text {and}} y> 0 {\ text {and}} x ^ {2 } + y ^ {2}> 1 \\ - \ pi - \ arcsin (\ sin (\ arcsin x + \ arcsin y)) = - \ pi - \ arcsin \ left (x {\ sqrt {1-y ^ { 2}}} + y {\ sqrt {1-x ^ {2}}} \ right) & {\ text {if}} x <0 {\ text {and}} y <0 {\ text {and}} x ^ {2} + y ^ {2}> 1 \\\ slutt {matrise}} \ høyre.}$${\ displaystyle \ arccos x + \ arccos y = \ left \ {{\ begin {matrix} \ arccos (\ cos (\ arccos x + \ arccos y)) = \ arccos \ left (xy - {\ sqrt {1- x ^ {2}}} {\ sqrt {1-y ^ {2}}} \ right) & {\ text {if}} x + y \ geq 0 \\ 2 \ pi - \ arccos (\ cos (\ arccos x + \ arccos y)) = 2 \ pi - \ arccos \ left (xy - {\ sqrt {1-x ^ {2}}} {\ sqrt {1-y ^ {2}}} \ right) & {\ text {if}} x + y <0 \\\ end {matrix}} \ right.}$

Det følger spesielt av dette for doble funksjonsverdier

${\ displaystyle 2 \ arcsin x = \ left \ {{\ begin {matrix} \ arcsin \ left (2x {\ sqrt {1-x ^ {2}}} \ right) & {\ text {if}} 2x ^ {2} \ leq 1 \\\ pi - \ arcsin \ left (2x {\ sqrt {1-x ^ {2}}} \ right) & {\ text {if}} x> 0 {\ text {and} } 2x ^ {2}> 1 \\ - \ pi - \ arcsin \ left (2x {\ sqrt {1-x ^ {2}}} \ right) & {\ text {if}} x <0 {\ text {and}} 2x ^ {2}> 1 \\\ slutt {matrise}} \ høyre.}$

${\ displaystyle 2 \ arccos x = \ left \ {{\ begin {matrix} \ arccos \ left (2x ^ {2} -1 \ right) & {\ text {if}} x \ geq 0 \\ 2 \ pi - \ arccos \ left (2x ^ {2} -1 \ right) & {\ text {if}} x <0 \\\ end {matrix}} \ right.}$

Derivater

Arcsine

${\ displaystyle {\ frac {\ mathrm {d}} {\ mathrm {d} x}} \ arcsin (x) = {\ frac {1} {\ sqrt {1-x ^ {2}}}}, \ qquad -1 <x <1}$

Arccosine

${\ displaystyle {\ frac {\ mathrm {d}} {\ mathrm {d} x}} \ arccos (x) = - {\ frac {1} {\ sqrt {1-x ^ {2}}}}, \ qquad -1 <x <1}$

omdannelse

${\ displaystyle {\ frac {\ mathrm {d}} {\ mathrm {d} x}} \ arccos (x) = - {\ frac {\ mathrm {d}} {\ mathrm {d} x}} \ arcsin (x)}$

Integraler

Arcsine

${\ displaystyle \ int \ arcsin \ left ({\ frac {x} {a}} \ right) \, \ mathrm {d} x = x \, \ arcsin \ left ({\ frac {x} {a}} \ right) + {\ sqrt {a ^ {2} -x ^ {2}}} + C}$

Arccosine

${\ displaystyle \ int \ arccos \ left ({\ frac {x} {a}} \ right) \, \ mathrm {d} x = x \, \ arccos \ left ({\ frac {x} {a}} \ right) - {\ sqrt {a ^ {2} -x ^ {2}}} + C}$

Komplekse argumenter

${\ displaystyle {\ begin {align} \ arcsin (a + b \, \ mathrm {i}) = \ quad {\ frac {\ operatorname {sgn ^ {+}} {a}} {2}} \ cdot \ arccos & \ left ({\ sqrt {(a ^ {2} + b ^ {2} -1) ^ {2} + 4b ^ {2}}} - (a ^ {2} + b ^ {2}) \ høyre) \\ + \; \ mathrm {i} \ cdot {\ frac {\ operatorname {sgn ^ {+}} {b}} {2}} \ cdot \ operatorname {arcosh} & \ left ({\ sqrt {(a ^ {2} + b ^ {2} -1) ^ {2} + 4b ^ {2}}} + (a ^ {2} + b ^ {2}) \ høyre) \ slutt {justert} }}$   Med ${\ displaystyle a, b \ in \ mathbb {R}}$

${\ displaystyle \ arccos (a + b \, \ mathrm {i}) = {\ frac {\ pi} {2}} - \ arcsin (a + b \, \ mathrm {i})}$

For funksjonen se Areakosinus hyperbolsk , og for funksjonen gjelder ${\ displaystyle \ operatorname {arcosh}}$${\ displaystyle \ operatorname {sgn ^ {+}} \ colon \ mathbb {R} \ to \ {- 1,1 \}}$

${\ displaystyle \ operatorname {sgn ^ {+}} (x): = 2 \ cdot \ Theta (x) -1 = {\ begin {cases} +1 & {\ text {for}} x \ geq 0 \\ - 1 og {\ text {for}} x <0 \ end {cases}}}$

med Heaviside-funksjonen . ${\ displaystyle \ Theta}$

Merknader

Viktige funksjonelle verdier

Se også: Sine og Cosine: Viktige funksjonsverdier

Tabellen nedenfor viser viktige funksjonsverdier for de to buefunksjonene .

${\ displaystyle x}$	${\ displaystyle \ arcsin (x)}$		${\ displaystyle \ arccos (x)}$
${\ displaystyle 0}$	${\ displaystyle 0 ^ {\ circ}}$	${\ displaystyle 0}$	${\ displaystyle 90 ^ {\ circ}}$	${\ displaystyle {\ frac {\ pi} {2}}}$
${\ displaystyle {\ frac {1} {2}}}$	${\ displaystyle 30 ^ {\ circ}}$	${\ displaystyle {\ frac {\ pi} {6}}}$	${\ displaystyle 60 ^ {\ circ}}$	${\ displaystyle {\ frac {\ pi} {3}}}$
${\ displaystyle {\ frac {1} {2}} {\ sqrt {2}}}$	${\ displaystyle 45 ^ {\ circ}}$	${\ displaystyle {\ frac {\ pi} {4}}}$	${\ displaystyle 45 ^ {\ circ}}$	${\ displaystyle {\ frac {\ pi} {4}}}$
${\ displaystyle {\ frac {1} {2}} {\ sqrt {3}}}$	${\ displaystyle 60 ^ {\ circ}}$	${\ displaystyle {\ frac {\ pi} {3}}}$	${\ displaystyle 30 ^ {\ circ}}$	${\ displaystyle {\ frac {\ pi} {6}}}$
${\ displaystyle 1}$	${\ displaystyle 90 ^ {\ circ}}$	${\ displaystyle {\ frac {\ pi} {2}}}$	${\ displaystyle 0 ^ {\ circ}}$	${\ displaystyle 0}$

Andre viktige verdier er:

${\ displaystyle x}$	${\ displaystyle \ arcsin (x)}$		${\ displaystyle \ arccos (x)}$
${\ displaystyle {\ tfrac {1} {4}} ({\ sqrt {6}} - {\ sqrt {2}})}$	${\ displaystyle 15 ^ {\ circ}}$	${\ displaystyle {\ tfrac {\ pi} {12}}}$	${\ displaystyle 75 ^ {\ circ}}$	${\ displaystyle {\ tfrac {5 \ pi} {12}}}$
${\ displaystyle {\ tfrac {1} {4}} \ left ({\ sqrt {5}} - 1 \ right)}$	${\ displaystyle 18 ^ {\ circ}}$	${\ displaystyle {\ tfrac {\ pi} {10}}}$	${\ displaystyle 72 ^ {\ circ}}$	${\ displaystyle {\ tfrac {2 \ pi} {5}}}$
${\ displaystyle {\ tfrac {1} {4}} {\ sqrt {10-2 {\ sqrt {5}}}}}$	${\ displaystyle 36 ^ {\ circ}}$	${\ displaystyle {\ tfrac {\ pi} {5}}}$	${\ displaystyle 54 ^ {\ circ}}$	${\ displaystyle {\ tfrac {3 \ pi} {10}}}$
${\ displaystyle {\ tfrac {1} {4}} \ left (1 + {\ sqrt {5}} \ right)}$	${\ displaystyle 54 ^ {\ circ}}$	${\ displaystyle {\ tfrac {3 \ pi} {10}}}$	${\ displaystyle 36 ^ {\ circ}}$	${\ displaystyle {\ tfrac {\ pi} {5}}}$
${\ displaystyle {\ tfrac {1} {4}} {\ sqrt {10 + 2 {\ sqrt {5}}}}}$	${\ displaystyle 72 ^ {\ circ}}$	${\ displaystyle {\ tfrac {2 \ pi} {5}}}$	${\ displaystyle 18 ^ {\ circ}}$	${\ displaystyle {\ tfrac {\ pi} {10}}}$
${\ displaystyle {\ tfrac {1} {4}} ({\ sqrt {6}} + {\ sqrt {2}})}$	${\ displaystyle 75 ^ {\ circ}}$	${\ displaystyle {\ tfrac {5 \ pi} {12}}}$	${\ displaystyle 15 ^ {\ circ}}$	${\ displaystyle {\ tfrac {\ pi} {12}}}$

Fortsatt bruddrepresentasjon av buesonen

I 1948 fant HS Wall følgende representasjon som en fortsatt brøkdel for buesinen :

${\ displaystyle \ arcsin (x) = {\ frac {x {\ sqrt {1-x ^ {2}}}} {1 - {\ cfrac {1 \ cdot 2x ^ {2}} {3 - {\ cfrac {1 \ cdot 2x ^ {2}} {5 - {\ cfrac {3 \ cdot 4x ^ {2}} {7 - {\ cfrac {3 \ cdot 4x ^ {2}} {9 - {\ cfrac {5 \ cdot 6x ^ {2}} {11- \ ldots}}}}}}}}}}}}}$

Kompleks funksjon

Buesonen og buesinen kan også uttrykkes av hovedgrenen til den komplekse logaritmen :

${\ displaystyle \ arcsin z = - \ mathrm {i} \, \ ln \ left (\ mathrm {i} z + {\ sqrt {1-z ^ {2}}} \ right)}$

${\ displaystyle \ arccos z = - \ mathrm {i} \, \ ln \ left (z + \ mathrm {i} {\ sqrt {1-z ^ {2}}} \ right)}$

Disse to formlene kan avledes som følger:

For : ${\ displaystyle \ arcsin z}$

${\ displaystyle {\ begin {align} \ sin (x) = {\ frac {\ mathrm {e} ^ {\ mathrm {i} x} - \ mathrm {e} ^ {- \ mathrm {i} x}} {2 \ mathrm {i}}} \\ {\ frac {\ mathrm {e} ^ {\ mathrm {i} x} - \ mathrm {e} ^ {- \ mathrm {i} x}} {2 \ mathrm {i}}} = z \\\ mathrm {e} ^ {\ mathrm {i} x} - {\ frac {1} {\ mathrm {e} ^ {\ mathrm {i} x}}} = 2z \ mathrm {i} \\ (\ mathrm {e} ^ {\ mathrm {i} x}) ^ {2} -1 = 2z \ mathrm {i} \ mathrm {e} ^ {\ mathrm {i} x} \ \ (\ mathrm {e} ^ {\ mathrm {i} x}) ^ {2} -2z \ mathrm {i} \ mathrm {e} ^ {\ mathrm {i} x} -1 = 0 \\\ mathrm {e} ^ {\ mathrm {i} x} = - {\ frac {-2z \ mathrm {i}} {2}} \ pm {\ sqrt {\ left ({\ frac {-2z \ mathrm {i} } {2}} \ right) ^ {2} - (- 1)}} \\\ mathrm {e} ^ {\ mathrm {i} x} = z \ mathrm {i} \ pm {\ sqrt {1- z ^ {2}}} \\\ mathrm {i} x = \ ln (z \ mathrm {i} \ pm {\ sqrt {1-z ^ {2}}}) \\ x = {\ frac {\ ln (z \ mathrm {i} \ pm {\ sqrt {1-z ^ {2}}})} {\ mathrm {i}}} \\ x = {\ frac {\ ln (z \ mathrm {i} ) \ pm {\ sqrt {1-z ^ {2}}}) \, \ mathrm {i}} {\ mathrm {i} ^ {2}}} \\ x = {\ frac {\ ln (z \ mathrm {i} \ pm {\ sqrt {1-z ^ {2}}}) \, \ mathrm {i}} {- 1}} \\ x = - \ mathrm {i} \, \ ln (z \ mathrm {i} \ pm {\ sqrt {1-z ^ {2}}}) \\\ arcsin z = - \ m athrm {i} \, \ ln (z \ mathrm {i} \ pm {\ sqrt {1-z ^ {2}}}) \\\ end {aligned}}}$

For : ${\ displaystyle \ arccos z}$

${\ displaystyle {\ begin {align} \ cos (x) = {\ frac {\ mathrm {e} ^ {\ mathrm {i} x} + \ mathrm {e} ^ {- \ mathrm {i} x}} {2}} \\ {\ frac {\ mathrm {e} ^ {\ mathrm {i} x} + \ mathrm {e} ^ {- \ mathrm {i} x}} {2}} = z \\\ mathrm {e} ^ {\ mathrm {i} x} + {\ frac {1} {\ mathrm {e} ^ {\ mathrm {i} x}}} = 2z \\ (\ mathrm {e} ^ {\ mathrm {i} x}) ^ {2} + 1 = 2z \ mathrm {e} ^ {\ mathrm {i} x} \\ (\ mathrm {e} ^ {\ mathrm {i} x}) ^ {2 } -2z \ mathrm {e} ^ {\ mathrm {i} x} + 1 = 0 \\\ mathrm {e} ^ {\ mathrm {i} x} = - {\ frac {-2z} {2}} \ pm {\ sqrt {\ left ({\ frac {-2z} {2}} \ right) ^ {2} -1)}} \\\ mathrm {e} ^ {\ mathrm {i} x} = z \ pm {\ sqrt {z ^ {2} -1}} \\\ mathrm {i} x = \ ln (z \ pm \ mathrm {i} {\ sqrt {1-z ^ {2}}}) \ \ x = {\ frac {\ ln (z \ pm \ mathrm {i} {\ sqrt {1-z ^ {2}}})} {\ mathrm {i}}} \\ x = {\ frac {\ ln (z \ pm \ mathrm {i} {\ sqrt {1-z ^ {2}}}) \, \ mathrm {i}} {\ mathrm {i} ^ {2}}} \\ x = {\ frac {\ ln (z \ pm \ mathrm {i} {\ sqrt {1-z ^ {2}}}) \, \ mathrm {i}} {- 1}} \\ x = - \ mathrm {i} \, \ ln (z \ pm \ mathrm {i} {\ sqrt {1-z ^ {2}}}) \\\ arccos z = - \ mathrm {i} \, \ ln (z \ pm \ mathrm { i} {\ sqrt {1-z ^ {2}}}) \\\ slutt {justert}}}$

Se også

• Trigonometri formel samling
• Trigonometriske funksjoner

litteratur

• Ilja Bronstein, Konstantin Semendjajew: Lommebok for matematikk . BG Teubner, Stuttgart 1991. ISBN 3-87144-492-8 .

Individuelle bevis

1. ↑ Eric W. Weisstein : Inverse trigonometriske funksjoner . På: MathWorld (engelsk).
2. ↑ George Hoever: Higher Mathematics compact . Springer Spektrum, Berlin Heidelberg 2014, ISBN 978-3-662-43994-4 ( begrenset forhåndsvisning i Google- boksøk ).