Mengdediagram

Bly-vindu med et Venn-diagram i Cambridge, England, hvor John Venns studerte

Settdiagrammer brukes til å grafisk illustrere mengdeori . Det er forskjellige typer settdiagrammer, spesielt Euler-diagrammer (etter Leonhard Euler ) og Venn-diagrammer (etter John Venn ).

Settdiagrammer kan bidra til å illustrere forholdet mellom settene, men er vanligvis uegnet som matematisk bevis . Bare settdiagrammer som representerer alle mulige relasjoner mellom settene som er representert, er egnet som bevis ; slike diagrammer kalles Venn-diagrammer. Ulempen med Venn-diagrammer er at hvis det er mer enn tre sett involvert, blir de fort forvirrende, fordi de med n objekter må representere 2 ⁿ muligheter. Venn selv kunne representere opptil fire, til slutt til og med fem, involverte sett ved hjelp av ellipser.

Eksempler

Euler-diagrammer

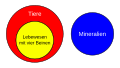
Euler-diagrammer brukes primært til å illustrere settteoretiske fakta, for eksempel delsettegenskapen. Følgende illustrasjoner er vanlige (hvorved mengdebetegnelsen i de tre følgende eksemplene ble plassert på linjen som omgir den og ikke - da det er mer fornuftig (se Euler-diagrammet for antall områder) - i avgrensningen av selve mengden; da og i det andre diagrammet er på samme side av grensen, kan man (mis-) forstå det slik at det betyr i (= område utenfor sirkelen)). ${\ displaystyle x}$${\ displaystyle A}$${\ displaystyle x}$${\ displaystyle A}$

• 

  ${\ displaystyle x \ i A}$; er et element av . ${\ displaystyle x}$${\ displaystyle A}$

• 

  ${\ displaystyle x \ notin A}$; er ikke et element av . ${\ displaystyle x}$${\ displaystyle A}$

• 

  ${\ displaystyle B \ delmengde A}$; er en delmengde av . ${\ displaystyle B}$${\ displaystyle A}$

Ytterligere eksempler på Euler-diagrammer er:

• 

  Euler-diagram over antall områder

• 

  Medlemskap av europeiske stater og ikke-europeiske stater i europeiske institusjoner

• 

  Euler Chart of the British Isles

• 

  Alle levende ting med fire ben er dyr, men ingen mineraler er et dyr.

Venn-diagrammer

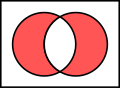
Venn-diagrammer viser alle sammenhenger mellom settene som vurderes. Derfor kan man lese av forbindelser fra dem og utlede eksistensen av andre relasjoner fra eksistensen av individuelle relasjoner.

• 

  ${\ displaystyle A \ cap B}$ (Kryss)

• 

  ${\ displaystyle A \ cup B}$ (Union sett)

• 

  ${\ displaystyle A \ setminus B}$ (Forskjell mengde)

• 

  ${\ displaystyle A \ bigtriangleup B}$( Symmetrisk forskjell )

• 

  ${\ displaystyle A ^ {\ rm {C}}}$( Utfylling av A)

Utvidelse til flere mengder

• 

  Venns konstruksjon med n = 3

• 

  Venns konstruksjon med n = 4

• 

  Venns konstruksjon med n = 5

• 

  Venns konstruksjon med n = 6

• 

  Venns elegante løsning med 4 ellipser

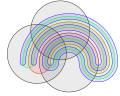
Venn-diagrammer er hovedsakelig kjent i representasjonen for tre sett med sirkler. Venn hadde imidlertid ambisjonen om å finne "elegante symmetriske figurer" som representerer et større antall sett, og han viste et diagram for fire sett i form av en ellips. Han ga deretter en konstruksjonsmetode som man kan vise Venn-diagrammer for "hvilket som helst" antall sett, med hver lukket kurve flettet sammen med de andre, med utgangspunkt i diagrammet med tre sirkler. En "slange" trekkes over den siste mengdevisningen. Dette kutter alle andre mengder.

Forskjeller mellom Venn- og Euler-diagrammer

Forskjellen mellom de to typene settdiagrammer blir spesielt tydelig hvis du ser på begge diagrammer for et spesifikt eksempel. Ta følgende tre mengder.

• ${\ displaystyle A = \ {1, \, 2, \, 5 \}}$
• ${\ displaystyle B = \ {1, \, 6 \}}$
• ${\ displaystyle C = \ {4, \, 7 \}}$

Euler- og Venn-diagrammene til disse tre settene ser slik ut.

• 

  Euler-diagram

• 

  venn diagram

Mens Euler-diagrammer bare viser de faktiske overlappene mellom mengdene, viser Venn-diagrammer alle mulige overlapp av områdene (selv om de ikke inneholder noen objekter).

Johnston Diagrammer

Johnston-diagrammer er en toverdis tolkning av settdiagrammer, spesielt Venn-diagrammer. I et Johnston-diagram tolkes en sirkel (sett) P som settet med omstendigheter der en påstand P er sann. Området utenfor sirkelen (komplementet til settet) P tolkes som settet med omstendigheter der utsagnet er falskt. For å si at en uttalelse er sann, må du male hele området utenfor sirkelen i svart; på denne måten indikerer man at omstendighetene som utsagnet ikke stemmer under, ikke kan gjelde. Omvendt, for å si at en uttalelse er falsk , må du male området i sirkelen i svart; det sies at omstendighetene som utsagnet er sant under ikke kan gjelde. Hvis du kombinerer to setninger P , Q ved en sammenheng , i. H. hvis man vil uttrykke at begge utsagnene er sanne, maler man hele området utenfor krysset mellom sirklene P , Q i svart; det sies at ingen av tilstandene der både P og Q ikke gjelder, kan eksistere.

Johnston-diagrammer er således en kartlegging av klassisk proposisjonslogikk til elementær mengde teori, hvor negasjonen blir representert som et komplement, sammenhengen som et skjæringspunkt og disjunksjonen som en union . Sannhetsverdiene sant og usant blir tilordnet henholdsvis det universelle settet og det tomme settet.

historie

Leibniz brukte allerede faste diagrammer for å representere syllogistikk rundt 1690 . Christian Weise , rektor ved grammatikkskolen i Zittau , brukte sette diagrammer for å representere logiske sammenhenger rundt 1700. Johann Christian Lange (1669–1756) ga ut boka Nucleus Logicae Weisianae i 1712 , der Weises logikk blir behandlet. Leonhard Euler , sveitsisk matematiker på 1700-tallet, introduserte Euler-diagrammet, som han først brukte i et brev datert 24. februar 1761.

John Venn , en britisk matematiker på 1800-tallet, introduserte Venn-diagrammet i 1881. I 1964 ble verk for Charles Sanders Peirce , som han skrev i siste kvartal av 1800-tallet, og som beskriver de eksistensielle grafene , anerkjent for første gang .

Søknadeksempler

Følgende grafikk viser hvordan Venn-diagrammer har blitt brukt til å illustrere syllogismer siden 1600-tallet . Gyldigheten av en konklusjon kan kontrolleres med denne metoden. (Så du kan for eksempel se at Modus Darapti bare er gyldig hvis det er et ikke-tomt mellombegrep .)

Det er ikke noe element i svarte områder ( generell uttalelse ).
I de røde områdene er det minst ett element x ( eksistensuttalelse ).

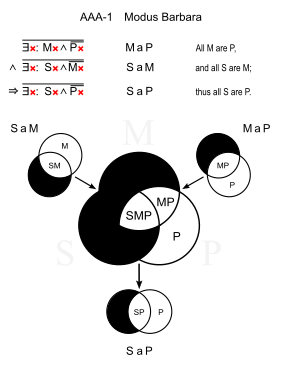
Bevis på modus Barbara ved bruk av Venn-diagrammer:   Det er ingen M utenfor P, det er ingen S utenfor M; så det er ingen S utenfor P.

Bevis på Modus Darii ved bruk av Venn-diagrammer:   Det er ingen M utenfor P, det er noen S i M; så det er noen S i P.

Slike Venn-diagrammer kan enkelt konverteres til Euler-diagrammer, som grafikken nedenfor viser. Venn-diagrammer har fordelen at man ikke kan glemme en overlapping, så de er også egnet for bevis. Med Euler-diagrammer er det derimot mer intuitivt å forstå hvilke mengder som ligger i hverandre eller hvilke som overlapper hverandre.

Venn-diagrammer og Euler-diagrammer

weblenker

Wiktionary: set diagram  - forklaringer av betydninger, ordets opprinnelse, synonymer, oversettelser

litteratur

• Gereon Wolters : Venn-diagrammer , i: Jürgen Mittelstraß (Hrsg.): Encyclopedia Philosophy and Philosophy of Science. 2. utgave. Volum 8: Th - Z. Stuttgart, Metzler 2018, ISBN 978-3-476-02107-6 , s. 280 f. (Med bibliografi).

Individuelle bevis

1. ^ De Formae Logicae per linearum ductus. ≈1690, kun publisert postumt i 1903 i: Couturat: Opuscules et fragmentes inedits de Leibniz. Pp. 292-321
2. ^ ^{A b} Moritz Wilhelm Drobisch : Logikk i henhold til dens enkleste proporsjoner. 5. utgave. Verlag Leopold Voss, Hamburg Leipzig 1887 s. 99
3. ↑ grifflogik.de , åpnet 30. august 2008