Geometrisk fokus

Det geometriske tyngdepunktet eller tyngdepunktet til en geometrisk figur (for eksempel en sirkelbue , trekant , kjegle ) er et spesielt særegen punkt som tolkes som et slags midtpunkt , selv med asymmetriske figurer. Matematisk tilsvarer dette gjennomsnittet av alle punkter i figuren. Spesielt kalles det geometriske tyngdepunktet til linjer også linjens tyngdepunkt , overflatene områdets tyngdepunkt og kroppene volumet tyngdepunktet . I enkle tilfeller kan tyngdepunktet oppnås gjennom geometriske betraktninger eller generelt beregnes ved hjelp av matematiske midler gjennom integrering . Metodene for analytisk geometri brukes til å beskrive kroppene . Tyngdepunktet er et gravitetssenter .

Det geometriske tyngdepunktet tilsvarer massesenteret til en fysisk kropp som består av homogent materiale, dvs. den har samme tetthet overalt . Det kan derfor også bestemmes rent mekanisk ved å balansere . Denne metoden kan brukes på modeller når det gjelder geografiske sentre på kontinenter eller land (for eksempel sentrum av Europa eller sentrum av Tyskland ).

Spesielt for det geografiske sentrum brukes noen ganger en annen definisjon, nemlig plasseringen av halveringslinjen for den respektive utvidelsen i geografisk lengdegrad og geografisk breddegrad.

I tilfelle av konkave linjer, overflater (for eksempel en veldig slank halvmåne ) eller kropper (for eksempel sigdverktøyet ), kan tyngdepunktet, midtpunktet eller midtpunktet også ligge utenfor det respektive objektet.

Geometrisk tyngdepunkt på endelig mange punkter i reelt vektorrom

Hvis det er par forskjellige punkter i et - vektorrom for et naturlig tall , blir deres geometriske tyngdepunkt definert som ${\ displaystyle \ mathbb {R}}$ ${\ displaystyle {\ mathcal {V}}}$ ${\ displaystyle m}$ ${\ displaystyle x_ {1}, \ prikker, x_ {m} \ i {\ mathcal {V}}}$${\ displaystyle s}$

${\ displaystyle s = {\ frac {1} {m}} {\ sum _ {i = 1} ^ {m} {x_ {i}}}}$  .

Konseptet med tyngdepunktet for en - dimensjonal simpleks${\ displaystyle k}$ faller inn i denne sammenhengen . Hvis en slik simpleks har hjørnepunktene , er dens tyngdepunkt ikke noe annet enn det geometriske tyngdepunktet til hjørnepunktene, dvs. ${\ displaystyle \ Delta \ subset \ mathbb {R} ^ {n} \; (k, n \ in \ mathbb {N} _ {0})}$ ${\ displaystyle v_ {0}, \ ldots, v_ {k} \ in \ mathbb {R} ^ {n}}$${\ displaystyle s _ {\ Delta}}$

${\ displaystyle s _ {\ Delta} = {\ frac {1} {k + 1}} {\ sum _ {i = 0} ^ {k} {v_ {i}}}}$  .

Tyngdepunktet til en slik simpleks er preget av det faktum at dens barsentriske koordinater er like i forhold til simpleksen, nemlig

${\ displaystyle = {\ frac {1} {k + 1}}}$

er.

Hvis disse endelig mange forskjellige punktene danner settet med alle hjørnepunktene til en geometrisk figur i det euklidiske rommet , kalles det geometriske tyngdepunktet til alle disse også hjørnet av tyngdepunktet til figuren. Eksempler på dette er spesielt segmentet , trekanten og tetraederet . For firkanter , ifølge Pierre de Varignon (1654–1722), er tyngdepunktet til hjørnet av en firkant også sentrum for de to senterlinjene , dvs. de to forbindelseslinjene til motsatte sidesentre.

Fokuspunkter for elementære geometriske figurer

I det følgende er noen fokuspunkter for elementære geometriske linjer, overflater og legemer spesifisert og delvis begrunnet av geometriske hensyn.

For aksialt symmetriske eller rotasjonssymmetriske figurer er spesifikasjonen av tyngdepunktet forenklet ved at den alltid ligger på symmetriaksen. I tilfelle av figurer med flere symmetriakser eller punktsymmetrisk objekter, slik som for eksempel en kvadratisk eller en sirkel, er fokuset ved skjæringspunktet mellom symmetriakser ( sentrum punkt ) i figuren.

Linjer

rute

Det geometriske tyngdepunktet til en linje er i sentrum, dvs. det er identisk med midtpunktet .

Sirkelbue

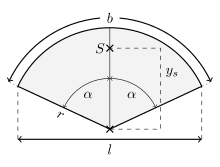
Hvis snittet av sirkelen roteres og forskyves på en slik måte at y-aksen til det kartesiske koordinatsystemet er en symmetriakse for den sirkelbue og sentrum av sirkelen ligger i koordinatets opprinnelse (se bilde), så tyngdepunktet kan føres gjennom

${\ displaystyle x_ {s} = 0 \ quad y_ {s} = {\ frac {2r ^ {2} \ sin \ alpha} {b}} = r {\ frac {l} {b}}}$

å beregne. Her er radius i sirkelen, lengden på sirkelbuen og den akkord lengde sirkelbuen. ${\ displaystyle r}$${\ displaystyle b}$${\ displaystyle l}$

${\ displaystyle 0 <\ alpha \ leq \ pi}$

For formelen mislykkes. Med tyngdepunktet kan det også beregnes for veldig små vinkler. ${\ displaystyle \ alpha = 0}$${\ displaystyle \ lim _ {\ alpha \ to 0} {\ tfrac {l} {b}} = \ cos \ alpha}$

Hvis sirkelen måtte forskyves eller roteres i begynnelsen, må det beregnede tyngdepunktet forskyves tilbake eller roteres tilsvarende for å fullføre beregningen.

Flat bue

For omtrent å beregne tyngdepunktet til en flat bue, må den forskyves i det kartesiske koordinatsystemet slik at midtpunktet på linjen som forbinder de to endepunktene, ligger i koordinatens opprinnelse. Da er tyngdepunktet litt under for en god tilnærming ${\ displaystyle h <r}$

${\ displaystyle z_ {s} \ approx {\ frac {2h} {3}}}$.

Ved (halvsirkel) er tyngdepunktet nøyaktig . Prosentavviket øker omtrent proporsjonalt med h og utgjør omtrent 4,7%. Dette etterfølges av uttrykket som indikerer tyngdepunktet i området med en nøyaktighet på bedre enn 5 promille. Den nøyaktige plasseringen av tyngdepunktet for linjen i hele området av finner du ved å sette inn i formelen for tyngdepunktet relatert til sentrum av sirkelen (se snittbuen ovenfor): ${\ displaystyle h = r}$${\ displaystyle {\ frac {2r} {\ pi}}}$${\ displaystyle h = r}$${\ displaystyle {\ frac {2000h} {3 (1000 + 47h / r)}}}$${\ displaystyle (0 \ leq h \ leq r)}$${\ displaystyle z_ {s} (h)}$${\ displaystyle (0 <h \ leq 2r)}$${\ displaystyle \ alpha = \ arccos (1-h / r)}$${\ displaystyle r \ sin (\ alpha) / \ alpha}$

${\ displaystyle z_ {s} = h-r + {\ frac {\ sqrt {h (2r-h)}} {\ arccos (1-h / r)}}}$.

Interessant, et maksimum viser litt større enn kl . Hvis et skifte eller rotasjon var nødvendig i begynnelsen, må tyngdepunktet flyttes tilbake tilsvarende. ${\ displaystyle z_ {s}}$${\ displaystyle r}$${\ displaystyle h \ approx 1 {,} 9r}$

Flate overflater

Når det gjelder flate overflater, kan tyngdepunktet generelt bestemmes ved å suspendere den utskårne overflaten på et punkt og tegne vinkelrett , en såkalt tyngdepunkt . Skjæringspunktet mellom to gravitasjonslinjer er fokus. Alle andre gravitasjonslinjer krysses også i dette fokuspunktet.
Når det gjelder polygoner (spesielt trekanter og firkanter), skilles det mellom tre forskjellige fokuspunkter, avhengig av naturen til den flate overflaten:

Areal tyngdepunkt, tyngdepunkt kant og hjørne tyngdepunkt

De to sistnevnte prioriteringene har imidlertid knapt noen praktisk anvendelse og er derfor mer eller mindre bare av akademisk interesse.
En homogen overflate med vilkårlig, men konstant tykkelse har (for å være presis) en sentroid ; imidlertid er man vanligvis fornøyd med begrepet fokus .
For en polygon, som bare består av grensene (z. B. av individuelle tynne plater eller i form av en tilsvarende bøyd ledning), hvis fokus er et tyngdepunkt
på en (fiktiv) modell der kroppens masse (polygonet) er bare konsentrert i hjørnene (f.eks. i form av kuler med samme vekt), man snakker om et hjørne tyngdepunkt .
Posisjonen til disse tre tyngdepunktene er den samme for polygoner med samme ytre form, men ovenfor. forskjellig natur, vanligvis forskjellig fra hverandre; deres avgjørelse avhenger av den enkelte sak.

triangel

Hjørnefokus

Hvis de kartesiske koordinatene til hjørnepunktene i trekanten er kjent, blir koordinatene til hjørnesentroid som aritmetisk gjennomsnitt : ${\ displaystyle ABC}$${\ displaystyle S = (x_ {s}, y_ {s})}$

${\ displaystyle x_ {s} = {\ frac {1} {3}} (x_ {A} + x_ {B} + x_ {C}),}$

${\ displaystyle y_ {s} = {\ frac {1} {3}} (y_ {A} + y_ {B} + y_ {C})}$

Man beregner det som er identisk med det felles punktet i tverrsnittet i trekanten. ${\ displaystyle S}$

Siden tyngdepunktet i hjørnet sammenfaller med tyngdepunktet i området til en trekant (se nedenfor), snakker man ganske enkelt om tyngdepunktet i trekanten.

Bildet viser hvordan man tegner tyngdepunktet.

De normaliserte barsentriske koordinatene til er . ${\ displaystyle S}$${\ displaystyle ({\ tfrac {1} {3}}: {\ tfrac {1} {3}}: {\ tfrac {1} {3}})}$

Uttrykt ved Trilineær koordinatene for hjørnet av tyngdekraften er en trekant med sider , ,${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle c}$

${\ displaystyle \ left ({\ frac {1} {a}}: {\ frac {1} {b}}: {\ frac {1} {c}} \ right) = (bc: ca: ab) \ ,.}$

Du kan også bruke lengden på den ene siden og høyden over den samme siden, f.eks. B. med og , bestem i kartesiske koordinater. Opprinnelsen til koordinatsystemet er i hjørnet (se illustrasjon). På denne måten kan de kartesiske koordinatene for tyngdepunktet føres gjennom ${\ displaystyle c}$${\ displaystyle h_ {c}}$${\ displaystyle A}$

${\ displaystyle x_ {s} = {\ frac {c + \ xi} {3}}, \ quad y_ {s} = {\ frac {h_ {c}} {3}}}$

å beregne.

Tyngdepunktet av en trekant er senter av Steiner ellipsen (Steiner umellipse) og Steiner inellipse .

Tyngdepunktet til en trekant er også det klart definerte punktet inne i trekanten, hvis tre forbindelseslinjer til hjørnepunktene i trekanten deler den i tre partielle trekanter med samme område (se barsentriske koordinater ).

Områdes tyngdepunkt = tyngdepunkt i hjørnet

Hvis man dekker en gitt trekant med rektangler som på bildet (som ved introduksjonen av den bestemte integralen), anerkjenner man ved hjelp av en strålesetning at tyngdepunktene (senterpunktene) til rektanglene alle ligger på halveringen . Dette betyr at tyngdepunktet til alle rektangler også er på denne halveringslinjen. Hvis den rektangulære dekningen nå er raffinert, beholdes eiendommen selv med en uendelig fin dekning. Så følgende gjelder: tyngdepunktet til trekanten ligger på halveringslinjen . Med analoge betraktninger følger det endelig: ${\ displaystyle ABC}$${\ displaystyle CM_ {c}}$${\ displaystyle CM_ {c}}$

Tyngdepunktet til en trekant er det felles punktet i halveringslinjen og dermed det samme som hjørnetes tyngdepunkt.

Kant tyngdepunkt

Den tyngdepunktet for den kant av en trekant (eller også: den tyngdepunktet av omkretsen av trekanten ) kan bestemmes geometrisk på en enkel måte, - det er dens Spieker punkt .

Trapes

Trapesformens tyngdepunkt kan konstrueres som følger: En tyngdekraftlinje halverer de to parallelle sidene. Et sekund kan oppnås ved å forlenge de parallelle sidene med lengden på den andre i motsatte retninger, og koble de to endepunktene sammen. Formelen i kartesiske koordinater er (målt fra nedre venstre hjørne):

${\ displaystyle {\ begin {align} x_ {s} & = {\ frac {a ^ {2} -b ^ {2} + \ xi (a + 2b)} {3 (a + b)}} \\ y_ {s} & = {\ frac {h} {3}} \ cdot {\ frac {a + 2b} {a + b}} \ end {align}}}$

Polygon

Tyngdepunktet til en ikke-veltet, lukket, også uregelmessig polygon med N hjørnepunkter kan beregnes som følger fra de kartesiske koordinatene til hjørnepunktene (nullpunktet for hjørnet og det femte hjørnepunktet er her). Hjørnepunktene nummereres fortløpende mot klokken. Tyngdepunktet til en vanlig polygon tilsvarer sentrum av omkretsen .${\ displaystyle (x_ {i}, y_ {i})}$${\ displaystyle (x_ {0}, y_ {0})}$${\ displaystyle N}$${\ displaystyle (x_ {N}, y_ {N})}$

Området til polygonet kan beregnes ved hjelp av den gaussiske trekantsformelen${\ displaystyle A}$

${\ displaystyle A = {\ frac {1} {2}} \ sum _ {i = 0} ^ {N-1} (x_ {i} \ y_ {i + 1} -x_ {i + 1} \ y_ {Jeg})}$

vær bestemt. Polygonets sentroid blir deretter gitt med formlene ${\ displaystyle S}$

${\ displaystyle {\ begin {align} x_ {s} & = {\ frac {1} {6A}} \ sum _ {i = 0} ^ {N-1} (x_ {i} + x_ {i + 1 }) (x_ {i} \ y_ {i + 1} -x_ {i + 1} \ y_ {i}) \\ y_ {s} & = {\ frac {1} {6A}} \ sum _ {i = 0} ^ {N-1} (y_ {i} + y_ {i + 1}) (x_ {i} \ y_ {i + 1} -x_ {i + 1} \ y_ {i}) \ end { justert}}}$

sikkert.

Seksjon av en sirkel

Hvis sirkelsnittet roteres og forskyves på en slik måte at y-aksen til det kartesiske koordinatsystemet er en symmetriakse for seksjonen og midtpunktet (for hele sirkelen) er ved opprinnelsen (se bilde) , så kan tyngdepunktet føres gjennom i radianer

${\ displaystyle y_ {s} = {\ frac {2r \ sin \ alpha} {3 \ alpha}} = {\ frac {2rl} {3b}}}$

med beregne.${\ displaystyle 0 <\ alpha \ leq \ pi}$

Hvis sirkelen måtte forskyves eller roteres i begynnelsen, må det beregnede tyngdepunktet flyttes tilbake eller roteres tilsvarende for å fullføre beregningen.

Sirkelsegment

For omtrent å beregne sentroid av et snitt av en sirkel, må det forskyves i det kartesiske koordinatsystemet slik at midtpunktet til linjen som forbinder de to endepunktene, ligger ved opprinnelsen til koordinatene. Så, til en god tilnærming , er tyngdepunktet litt over ${\ displaystyle h <r}$

${\ displaystyle z_ {s} \ approx {\ frac {2h} {5}}}$.

Ved (halvsirkel) er tyngdepunktet nøyaktig . Prosentavviket øker omtrent proporsjonalt med h og er omtrent 5,8%. Dette etterfølges av uttrykket som indikerer tyngdepunktet i området med en nøyaktighet på bedre enn 5 promille. Den nøyaktige plasseringen av tyngdepunktet i hele området av finner du ved å sette inn i formelen for tyngdepunktet relatert til sentrum av sirkelen  : ${\ displaystyle h = r}$${\ displaystyle {\ frac {4r} {3 \ pi}}}$${\ displaystyle h = r}$${\ displaystyle {\ frac {200h} {500-29h / r}}}$${\ displaystyle (0 \ leq h \ leq r)}$${\ displaystyle z_ {s} (h)}$${\ displaystyle (0 <h \ leq 2r)}$${\ displaystyle \ alpha = \ arccos (1-h / r)}$${\ displaystyle 4r \ sin (\ alpha) ^ {3} / (6 \ alpha -3 \ sin (2 \ alpha))}$

${\ displaystyle z_ {s} = h-r + {\ frac {2 \ left ({\ sqrt {h (2r-h)}} \ right) ^ {3}} {3 \ left ((hr) {\ sqrt { h (2r-h)}} + r ^ {2} \ arccos (1-h / r) \ høyre)}}$.

Hvis et skifte eller rotasjon var nødvendig i begynnelsen, må tyngdepunktet flyttes tilbake tilsvarende.

kropp

For tredimensjonale legemer kan man beregne både volumet tyngdepunkt, dvs. tyngdepunktet til det faste legemet, og arealet tyngdepunktet, dvs. tyngdepunktet til området som avgrenser kroppen.

Pyramide og kjegle

For å beregne tyngdepunktet til volumet og sentrum av arealet til en pyramide eller en kjegle , forskyves det i det skrå koordinatsystemet slik at tyngdepunktet til basisområdet ligger i opprinnelsen til koordinatene og y-aksen går gjennom toppunktet. Da kan tyngdepunktet til en pyramide eller en kjegle gå gjennom${\ displaystyle (0,0,0)}$

${\ displaystyle x_ {s} = 0, \ qquad y_ {s} = {\ frac {h} {4}}, \ qquad z_ {s} = 0}$

og tyngdepunktet til den laterale overflaten gjennom

${\ displaystyle x_ {s} = 0, \ qquad y_ {s} = {\ frac {h} {3}}, \ qquad z_ {s} = 0}$

beregnes.

Paraboloid av revolusjon

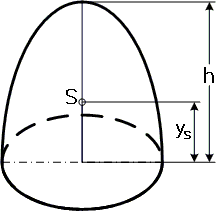
For å beregne tyngdepunktet av volumet og sentrum av området av en paraboloid omdreinings, forskyves den i det kartesiske koordinatsystem, slik at tyngdepunktet av sokkelområdet ligger i origo for koordinatene . Deretter kan du gå gjennom tyngdepunktet til volumet til revolusjonens paraboloid ${\ displaystyle (0,0,0)}$

${\ displaystyle x_ {s} = 0, \ qquad y_ {s} = {\ frac {h} {3}}, \ qquad z_ {s} = 0}$

å beregne. Centroid ser litt mer komplisert ut. For komponentene og gjelder også igjen ${\ displaystyle x_ {s}}$${\ displaystyle z_ {s}}$

${\ displaystyle x_ {s} = z_ {s} = 0}$

og komponenten er inkludert ${\ displaystyle y_ {s}}$

${\ displaystyle y_ {s} = h - {\ frac {4 \ pi {\ sqrt {f}} \ int _ {0} ^ {h} y {\ sqrt {f + y}} \, \ mathrm {d } y} {4 \ pi {\ sqrt {f}} \ int _ {0} ^ {h} {\ sqrt {f + y}} \, \ mathrm {d} y}} = h \ left (1+ {\ frac {2} {5}} (f / h) - {\ frac {3/5} {1-1 / (1 + h / f) ^ {3/2}}} til høyre),}$

hvor uttrykket i nevneren av den første fraksjonen representerer overflaten av parabolen åpnet til høyre med brennvidden f. Ab strever mot , ellers mot . ${\ displaystyle y = 2 {\ sqrt {fx}}}$${\ displaystyle (f / h) \ gtrsim 3}$${\ displaystyle y_ {s}}$${\ displaystyle {\ tfrac {1} {2}} h}$${\ displaystyle {\ tfrac {2} {5}} h}$

Sfærisk segment

For å beregne tyngdepunktet til volumet og sentroidet til et sfærisk segment , blir segmentet forskjøvet i det kartesiske koordinatsystemet slik at sentrum av den faste sfæren ligger i koordinatens opprinnelse . Tyngdepunktet er da gjennom${\ displaystyle (0,0,0)}$

${\ displaystyle x_ {s} = 0, \ quad y_ {s} = {\ frac {3 (2r-h) ^ {2}} {4 (3r-h)}}, \ quad z_ {s} = 0 }$

og tyngdepunktet gjennom

${\ displaystyle x_ {s} = 0, \ quad y_ {s} = r - {\ frac {h} {2}}, \ quad z_ {s} = 0}$

regnet ut. ( ) ${\ displaystyle 0 \ leq h \ leq 2 \, r}$

Oppsummer viktige områder

Det er mulig å kombinere flere fokuspunkter for individuelle figurer til et felles fokuspunkt for den totale figuren, slik at fokuspunktet til en sammensatt figur resulterer fra fokuspunktene til individuelle enkle elementer.

endimensjonalt	todimensjonal	tredimensjonalt	som regel
${\ displaystyle x_ {s} = {\ frac {\ sum \ limits _ {i} (x_ {s, i} \ cdot l_ {i})} {\ sum \ limits _ {i} l_ {i}}} }$	${\ displaystyle x_ {s} = {\ frac {\ sum \ limits _ {i} (x_ {s, i} \ cdot A_ {i})} {\ sum \ limits _ {i} A_ {i}}} }$ ${\ displaystyle y_ {s} = {\ frac {\ sum \ limits _ {i} (y_ {s, i} \ cdot A_ {i})} {\ sum \ limits _ {i} A_ {i}}} }$	${\ displaystyle x_ {s} = {\ frac {\ sum \ limits _ {i} (x_ {s, i} \ cdot V_ {i})} {\ sum \ limits _ {i} V_ {i}}} }$ ${\ displaystyle y_ {s} = {\ frac {\ sum \ limits _ {i} (y_ {s, i} \ cdot V_ {i})} {\ sum \ limits _ {i} V_ {i}}} }$ ${\ displaystyle z_ {s} = {\ frac {\ sum \ limits _ {i} (z_ {s, i} \ cdot V_ {i})} {\ sum \ limits _ {i} V_ {i}}} }$	${\ displaystyle {\ vec {r}} _ {s} = {\ frac {\ sum \ limits _ {i} ({\ vec {r}} _ {s, i} \ cdot V_ {i})} { \ sum \ limits _ {i} V_ {i}}}}$

Koordinatene , og skal spesifiseres i et fritt valgbart, men enhetlig kartesisk koordinatsystem. Hvis en overflate (et legeme) har utsparinger, kan også sumformlene ovenfor brukes, med tanke på at de innfelte overflatene (volumene) er inkludert i beregningen med et negativt tegn . Komponentene i tyngdepunktet danner vektoren . ${\ displaystyle x_ {s}}$${\ displaystyle y_ {s}}$${\ displaystyle z_ {s}}$${\ displaystyle x_ {s}, \, y_ {s}, \, z_ {s}}$ ${\ displaystyle {\ vec {r}} _ {s}}$

Definisjon av tyngdepunktet med integraler

Formlene for beregning av tyngdepunktet til elementære geometriske figurer kan utledes ved hjelp av integralene gitt nedenfor. Når det gjelder mer kompliserte figurer, kan disse integralene ofte bare bestemmes numerisk .

Definisjonen tilsvarer matematisk gjennomsnittet av alle punkter i det geometriske objektet (kroppen) i det euklidiske rommet . Når det gjelder linjer og områder i todimensjonalt rom , bare koordinatene og som skal beregnes, er koordinaten ikke aktuelt. Integreringsområdet er endimensjonalt for linjer, todimensjonalt for overflater og tredimensjonalt for kropper. ${\ displaystyle \ mathbb {R} ^ {3}}$${\ displaystyle \ mathbb {R} ^ {2}}$${\ displaystyle x_ {S}}$${\ displaystyle y_ {S}}$${\ displaystyle z}$

linje

For en linje av lengde tyngdepunktet er gitt av ${\ displaystyle C}$ ${\ displaystyle L}$${\ displaystyle {\ vec {r}} _ {S} = (x_ {S}, y_ {S}, z_ {S})}$

${\ displaystyle x_ {S} = {\ frac {1} {L}} \ int _ {C} x \, \ mathrm {d} s, \ quad y_ {S} = {\ frac {1} {L} } \ int _ {C} y \, \ mathrm {d} s, \ quad z_ {S} = {\ frac {1} {L}} \ int _ {C} z \, \ mathrm {d} s}$

Med

${\ displaystyle \ quad L = \ int _ {C} \, \ mathrm {d} s.}$

Disse integralene er stiintegraler av den første typen .

Overflater

For et område med areal er tyngdepunktet definert av ${\ displaystyle F}$ ${\ displaystyle A}$

${\ displaystyle x_ {S} = {\ frac {1} {A}} \ int _ {F} x \, \ mathrm {d} A, \ quad y_ {S} = {\ frac {1} {A} } \ int _ {F} y \, \ mathrm {d} A, \ quad z_ {S} = {\ frac {1} {A}} \ int _ {F} z \, \ mathrm {d} A}$

Med

${\ displaystyle \ quad A = \ int _ {F} \ mathrm {d} A.}$

Disse integralene er overflateintegraler med et skalar overflateelement.

kropp

Når det gjelder et begrenset legeme i et tredimensjonalt rom med volum , defineres tyngdepunktet av ${\ displaystyle K}$ ${\ displaystyle V}$

${\ displaystyle x_ {S} = {\ frac {1} {V}} \ int _ {K} x \, \ mathrm {d} V, \ quad y_ {S} = {\ frac {1} {V} } \ int _ {K} y \, \ mathrm {d} V, \ quad z_ {S} = {\ frac {1} {V}} \ int _ {K} z \, \ mathrm {d} V}$

Med

${\ displaystyle \ quad V = \ int _ {K} \ mathrm {d} V.}$

Disse integralene er volumintegraler .

Som regel

Vær en kropp med volum . Fokuset på defineres av ${\ displaystyle K \ subset \ mathbb {R} ^ {n}}$${\ displaystyle V}$${\ displaystyle x_ {S} = (x_ {s, 1}, \ ldots, x_ {s, n}) \ in \ mathbb {R} ^ {n}}$${\ displaystyle K}$

${\ displaystyle x_ {s, i} = {\ frac {1} {V}} \ int _ {K} x_ {i} \, \ mathrm {d} V \ \ quad {\ text {with}} \ quad V = \ int _ {K} \ mathrm {d} V,}$

hvor er det m-dimensjonale volumelementet og dimensjonen til , er med .${\ displaystyle \ mathrm {d} V}$${\ displaystyle m}$${\ displaystyle K}$${\ displaystyle m \ leq n}$

Integrasjon med symmetriske gjenstander

Når det gjelder objekter, er symmetrielementene, f.eks. B. har en symmetriakse eller et symmetriplan , beregningen av tyngdepunktet forenkles i mange tilfeller, siden tyngdepunktet alltid er inneholdt i symmetrielementet. Hvis objektet har en symmetriakse, kan volumelementet uttrykkes som en funksjon av det uendelige akseelementet. Det trenger bare å integreres via symmetriaksen.

Alternativ integrert formel for områder i ${\ displaystyle \ mathbb {R} ^ {2}}$

En annen mulighet til å beregne koordinatene til et områdes tyngdepunkt er resultat av formlene:

${\ displaystyle x_ {s} = {\ frac {\ int _ {a} ^ {b} (x (f (x) -g (x))) \, \ mathrm {d} x} {\ int _ { a} ^ {b} (f (x) -g (x)) \, \ mathrm {d} x}}}$, ${\ displaystyle y_ {s} = {\ frac {\ int _ {a} ^ {b} ((f (x)) ^ {2} - (g (x)) ^ {2}) \, \ mathrm { d} x} {\ int _ {a} ^ {b} (2 (f (x) -g (x))) \, \ mathrm {d} x}},}$

hvor grensene og skjæringspunktene mellom funksjonene og representerer. Denne formelen kan brukes til å beregne tyngdepunktet til en hvilken som helst flat overflate som er lukket mellom to funksjoner. Vilkårene for dette er ,${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle f (x)}$${\ displaystyle g (x)}$${\ displaystyle a <x <b}$${\ displaystyle g (x) <y <f (x).}$

Eksempler på integrert kalkulator

Linjens tyngdepunkt for en bue

Den enkleste måten å spesifisere punkter på en flat sirkelbue er i polare koordinater . Hvis y-aksen ligger på symmetrilinjen med opprinnelsen i sentrum av sirkelen, er koordinatene:

${\ displaystyle x = r \ sin \ varphi, \, y = r \ cos \ varphi.}$

Lengden på buen skyldes: ${\ displaystyle b}$

${\ displaystyle b = \ int _ {K} \ mathrm {d} s = \ int _ {- \ alpha} ^ {\ alpha} r \ mathrm {d} \ varphi = 2r \ alpha,}$

der elementet med uendelig lengde kan erstattes av. ${\ displaystyle \ mathrm {d} s}$${\ displaystyle r \ mathrm {d} \ varphi}$

Av hensyn til symmetri er . For y-koordinaten til linjen resulterer centroid fra definisjonsligningen: ${\ displaystyle x_ {S} = 0}$

${\ displaystyle y_ {S} = {\ frac {1} {b}} \ int _ {K} y \, \ mathrm {d} s = {\ frac {1} {b}} \ int _ {- \ alfa} ^ {\ alpha} r ^ {2} \ cos \ varphi \, \ mathrm {d} \ varphi.}$

Integreringen innenfor grensene resulterer da

${\ displaystyle y_ {S} = {\ frac {r ^ {2}} {b}} 2 \ sin \ alpha = r {\ frac {l} {b}}.}$

Tyngdepunkt for en parabel

For den praktiske bestemmelsen av x-koordinaten til tyngdepunktet i det todimensjonale tilfellet, erstatt med , som tilsvarer en uendelig minimal overflatestripe. Videre tilsvarer dette funksjonen som avgrenser området . ${\ displaystyle \ mathrm {d} A}$${\ displaystyle y \ cdot \ mathrm {d} x}$${\ displaystyle y}$${\ displaystyle y (x)}$

For den praktiske beregningen av y-koordinaten i det todimensjonale tilfellet er det i utgangspunktet to tilnærminger:

• Enten danner man den inverse funksjonen og beregner integralet , hvorved de "nye" integrasjonsgrensene nå kan bli funnet på y-aksen,${\ displaystyle x (y)}$${\ displaystyle \ textstyle \ int _ {A} y \ mathrm {d} A = \ int _ {y} y \ cdot x (y) \ \ mathrm {d} y}$
• eller man utnytter det faktum at tyngdepunktet til hver uendelig minimal overflatestripe parallelt med y-aksen er. Deretter oppnås en enklere formel for å bestemme y-koordinaten, ved hjelp av hvilken dannelsen av den inverse funksjonen lagres:${\ displaystyle {\ tfrac {y (x)} {2}}}$

Vi ser etter tyngdepunktet til området som er definert av en parabel og x-aksen (se tilstøtende figur). ${\ displaystyle y = x ^ {2} -4}$

Først bestemmer vi innholdet i området ${\ displaystyle A}$

${\ displaystyle A = \ left | \ int \ limits _ {- 2} ^ {2} (x ^ {2} -4) \, \ mathrm {d} x \ right | = {\ frac {32} {3 }}}$

Grensene for integralet er nollene til funksjonen når området er begrenset av x-aksen.

Den koordinaten for sentrum av tyngdekraften fører ${\ displaystyle x}$

${\ displaystyle x_ {s} = {\ frac {1} {A}} \ int \ limits _ {- 2} ^ {2} \ int \ limits _ {y (x)} ^ {0} x \, \ mathrm {d} y \, \ mathrm {d} x = - {\ frac {1} {A}} \ int \ limits _ {- 2} ^ {2} x \ cdot y (x) \, \ mathrm { d} x = - {\ frac {1} {A}} \ int \ limits _ {- 2} ^ {2} x \ cdot (x ^ {2} -4) \, \ mathrm {d} x = 0 .}$

Den koordinere resultater i ${\ displaystyle y}$

${\ displaystyle y_ {s} = {\ frac {1} {A}} \ int \ limits _ {- 2} ^ {2} \ int \ limits _ {y (x)} ^ {0} y \, \ mathrm {d} y \, \ mathrm {d} x = - {\ frac {1} {2A}} \ int \ limits _ {- 2} ^ {2} y (x) ^ {2} \, \ mathrm {d} x = - {\ frac {1} {2A}} \ int \ limits _ {- 2} ^ {2} (x ^ {4} -8x ^ {2} +16) \, \ mathrm {d } x = -1 {,} 6.}$

Se også

• Commandinos teorem
• Bisektor

litteratur

• Hermann Athens, Jörn Bruhn (red.): Leksikon for skolematematikk og relaterte områder . teip 4 : S til Z. Aulis Verlag, Köln 1978, ISBN 3-7614-0242-2 , s. 943-944 . 
• HSM Coxeter: Immortal Geometry . Oversatt til tysk av JJ Burckhardt (=  Vitenskap og kultur . Bind 17 ). Birkhäuser Verlag, Basel, Stuttgart 1963 ( MR0692941 ). 
• Egbert Harzheim : Introduksjon til kombinatorisk topologi (=  matematikk. Introduksjoner til emnet og resultater av delområdene og relaterte vitenskaper ). Scientific Book Society, Darmstadt 1978, ISBN 3-534-07016-X ( MR0533264 ). 
• Jens Levenhagen, Manfred Spata: Bestemmelsen av områdesentre . I: Vermessungswesen und Raumordnung Bind 60, 1998, s. 31–42.
• Harald Scheid (red.) : DUDEN: Rechnen und Mathematik . 4., fullstendig revidert utgave. Bibliografisk institutt , Mannheim / Wien / Zürich 1985, ISBN 3-411-02423-2 . 
• Thomas Westermann: Matematikk for ingeniører . Springer 2011, ISBN 978-3-642-12759-5 , s. 336–338, ( utdrag fra Googles boksøk )

weblenker

• Fokus på figurer på mathematische-basteleien.de
• Massesenter på Pauls online matematiske notater - Calculus II, Lamar University
• Utledning av formler for fokus på trekanten
• Flash-animasjon for fokuskonstruksjonen av trekanten (dwu-læremateriell)

Individuelle bevis

1. ↑ Monument for separasjonen av Tirol for 100 år siden orf.at, 10. oktober 2020, åpnet 10. oktober 2020. - Markstein midt i Tirol (...) . "Hvis et rektangel er plassert rundt grensene til det historiske Tirol og to diagonaler er tegnet i det, er sentrum av det historiske Tirol i Latzfons ...".
2. ↑ Egbert Harzheim: Introduksjon til kombinatorisk topologi. 1978, s. 31 ff.
3. ^ Hermann Athen, Jörn Bruhn (red.): Leksikon for skolematematikk og relaterte områder . Volum 4: S til Z. 1978, s. 944
4. ↑ Coxeter, op.cit., S. 242
5. ↑ DUDEN: regning og matematikk. 1985, s. 652
6. ↑ Alfred Böge, teknisk mekanikk . Vieweg + Teubner 2009, s. 84 ( begrenset forhåndsvisning i Google-boksøk)
7. ^ Alfred Böge: Teknisk mekanikk . Vieweg + Teubner, Wiesbaden 2011, ISBN 978-3-8348-1355-8 , pp. 77 . 
8. ↑ Friedrich Joseph Pythagoras Riecke (red.): Mathematische Unterhaltungen. Første utgave. 1973, s. 76
9. ↑ Rieckes bevis (og et annet bevis) finnes i bevisarkivet .
10. ↑ Beregning av arealet og midtpunktet til en polygon ( Memento fra 22. september 2009 i Internet Archive )
11. ^ Lothar Papula: Matematisk formulesamling for ingeniører og naturforskere . Vieweg, Wiesbaden 2006, ISBN 978-3-8348-0156-2 , pp. 32-38 . 
12. ↑ Frank Jablonski: Focus ( Memento fra 11. desember 2009 i Internet Archive ), Universitetet i Bremen, s. 114 (PDF; 688 kB)
13. ^ Alfred Böge et al.: Håndbok for maskinteknikk: Grunnleggende og anvendelser av maskinteknikk . Springer 2013, side C14, Gl. (39)
14. ↑ s. 34
15. ↑ s. 38
16. ↑ Centroid . I: M. Hazewinkel: Encyclopedia of Mathematics . ("Center of a compact set")
17. ↑ Norbert Henze , Günter Last: Matematikk for industrielle ingeniører og for vitenskapelig-tekniske kurs - bind II . Vieweg + Teubner, 2004, ISBN 3-528-03191-3 , s. 128 ( utdrag i Googles boksøk )
18. ↑ David Halliday: Fysikk / David Halliday; Robert Resnick; Jearl Walker. Redigert av den tyske oversetteren Stephan W. Koch. [Oversetteren Anna Schleitzer ...] Wiley-VCH-Verlag, Weinheim 2007, ISBN 978-3-527-40746-0 , s. 192 ( begrenset forhåndsvisning i Google Book-søk). 
19. ^ Thomas Westermann: Matematikk for ingeniører . Springer 2011, ISBN 978-3-642-12759-5 , s. 338 ( utdrag i Googles boksøk).